L’idée intuitive à la base de l’homologie à la Poincaré

Ordre de connexion d’une surface et généralisations

Pour décrire la forme des surfaces fermées, Riemann avait introduit dans sa thèse la notion d’ordre de connexion. Des brouillons de Riemann et des lettres de Betti montrent qu’ils ont tous les deux essayé de généraliser cette notion à des variétés de dimension arbitraire. Leurs tentatives de définitions sont cependant restées assez floues. Dans son mémoire Sur l’Analysis Situs, Poincaré introduit le concept d’homologie, qui permet de mesurer la complexité de la forme d’une variété de dimension arbitraire. Les ordres de connexions apparaissent naturellement dans ce cadre.

L’ordre de connexion d’une surface fermée orientable $S$ peut être défini de plusieurs manières. On peut tout d’abord choisir un point $x\in S$, et découper $S$ le long de courbes fermées simples passant par $x$. L’ordre de connexion de $S$ est alors le nombre de courbes nécessaires pour obtenir un disque après découpage.

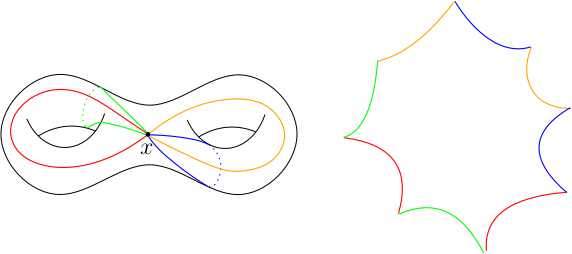
Première définition de l’ordre de connexion d’une surface

Il faut 4 courbes fermées simples passant par $x$ pour découper cette surface en un disque topologique

La définition ci-dessus repose entre autres sur le fait que les courbes sont de codimension $1$ dans la surface $S$. Elle se généralise ainsi très mal au cas où $S$ est une variété de dimension $m>2$, du moins si on veut remplacer les courbes tracées sur $S$ par des sous-variétés de $S$ de dimensions arbitraires.

On peut aussi essayer de définir l’ordre de connexion d’une surface fermée $S$ comme l’entier minimal $k$ vérifiant la propriété suivante : si on considère $k+1$ courbes fermées simples quelconques sur $S$, alors certaines de ces courbes, correctement orientées, formeront le bord orienté d’un morceau [1] de $S$

Seconde définition de l’ordre de connexion d’une surface

On trace cinq courbes fermées simples sur la surface S considérée. Certaines de ces courbes, correctement orientées, forment la frontière orientée d’un morceau de la surface S (en l’occurence la ``moitié supérieure" de S). Ce n’est plus vrai si on considère quatre courbes au lieu de cinq.

Cette seconde définition semble beaucoup plus apte à la généralisation en dimension supérieure, comme l’avait déjà remarqué Riemann. Cela conduit à l’idée intuitive qui va donner naissance au concept d’homologie :

On veut mesurer la complexité de la topologie d’une variété $X$ en comptant, pour chaque entier $p$ entre $0$ et $\mathrm{dim}(X)$, l’entier minimal $k$ avec la propriété suivante : si on considère $k+1$ sous-variétés fermées de dimension $p$ de $X$, alors certaines de ces sous-variétés, correctement orientées, formeront le bord orienté d’un « morceau » de $X$ de dimension $p+1$.

Autrement dit :

On veut mesurer la complexité de la topologie d’une variété $X$ en comptant, pour chaque entier $p$ entre $0$ et $\mathrm{dim}(X)$, le nombre maximal $k$ de sous-variétés fermées de dimension $p$ que l’on peut « faire entrer » dans $X$, sans que certaines de ces sous-variétés, correctement orientées, ne forment le bord orienté d’un « morceau » de $X$ de dimension $p+1$.

Pour donner un sens précis à cette idée intuitive, il faut préciser le sens de l’expression « forment le bord orienté d’un morceau de $S$ de dimension $p+1$ ». La première idée qui vient à l’esprit est de traduire simplement « morceau de $S$ de dimension $p+1$ » par « sous-variété compacte à bord de dimension $p+1$ de $S$ ». Hélas, on s’aperçoit bien vite que ce choix n’a guère d’intérêt : il conduit à une « complexité de la topologie d’une variété $X$ » qui est presque toujours infinie !

Un exemple

Considérons le cas $X=\mathbb{T}^2$ et $p=1$. Les sous-variétés (connexes) sans bord de dimension un de $\mathbb{T}^2$ sont des courbes fermées simples. Considérons une collection de telles courbes orientées $C_1,\dots,C_\ell$, où chaque $C_i$ est la projection dans $\mathbb{T}^2=\mathbb{R}^2/\mathbb{Z}^2$ d’une droite affine de pente rationnelle de $\mathbb{R}^2$, les pentes de ces droites étant deux à deux distinctes. Nous avons dessiné un exemple d’une telle collection de courbes orientées ci-dessous (le tore est représenté comme un carré, dont il faut identifier mentalement les côtés opposés).

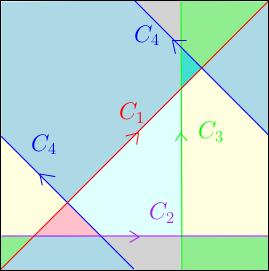
Une famille de courbes fermées simples dans le tore

Les sous-variétés à bord de dimension $p+1$ de $\mathbb{T}^2$ sont des sous-surfaces à bord. Si $\Sigma$ est une sous-surface compacte à bord (lisse) de $\mathbb{T}^2$, et si le bord de $\Sigma$ est contenu dans $C_1\cup\dots\cup C_\ell$, alors chaque composante de bord de $\Sigma$ est exactement l’une des courbes $C_1,\dots,C_\ell$ (en effet, les courbes $C_1,\dots,C_\ell$ se croisent avec angle non-nul à chaque point d’intersection ; par conséquent les seules courbes fermées lisses contenues dans $C_1\cup\dots\cup C_\ell$ sont les courbes $C_1,\dots,C_\ell$ elles-mêmes). Pour chaque entier $i$, la courbe fermée $C_i$ n’est pas, à elle seule, le bord d’une sous-surface compacte à bord $\Sigma$ de $\mathbb{T}^2$. Enfin, si $i$ et $j$ sont deux entiers distincts, les courbes $C_i$ et $C_j$ s’intersectent ; elles ne peuvent donc pas être des composantes de bord d’une même sous-surface compacte à bord de $\mathbb{T}^2$. Ainsi, on ne peut pas trouver une sous-surface compacte à bord $\Sigma$ de $\mathbb{T}^2$, tel que le bord de $\Sigma$ soit constitué de certaines des courbes $C_1,\dots,C_\ell$.

On voit donc que, si, dans l’idée intuitive ci-dessus, on traduit « morceau de $\mathbb{T}^2$ de dimension 2 » par « sous-variété compacte à bord de dimension 2 de $\mathbb{T}^2$ », alors la « complexité » du tore $\mathbb{T}^2$ sera au moins égale à $\ell$. Comme l’entier $\ell$ est aussi grand qu’on veut... la « complexité » de $\mathbb{T}^2$ sera infinie !

Pourtant, sur le dessin ci-dessus, les courbes $C_i$ découpent le tore $\mathbb{T}^2$ en polygones, et on a envie de dire que les courbes $C_i$, quitte à les couper en morceaux, forment le bord de ces polygones.

Conséquences

L’exemple ci-dessus suggère :

1. d’élargir la classe des sous-variétés à bord afin d’y inclure les polygones, et plus généralement des « sous-variétés » dont le bord comportera des faces, des arêtes, des sommets, etc.. C’est ce que nous ferons en introduisant la notion de sous-variété polyédrale, qui correspond, à notre avis, à la notion de « variété » que Poincaré cherche à définir --- sans y parvenir formellement --- dans les premiers paragraphes de l’Analysis Situs (voir nos commentaires).
2. de s’autoriser à découper les sous-variétés en morceaux. Dans ce but, nous définirons une notion de subdivision d’une sous-variété polyédrale, et nous identifierons chaque sous-variété polyédrale à n’importe laquelle de ses subdivisions. Comme expliqué ici, nous pensons que cette identification est tacite chez Poincaré.