L’identification entre les deux définitions du groupe fondamental

Commençons par brièvement présenter la définition du groupe fondamental qui est devenue la plus traditionnelle et qui est sans aucun doute la plus facile pour un accès direct. Cette définition, détaillée ici, présente deux inconvénients majeurs. Le premier est que cette définition ne présente pas ce groupe comme ce qu’il devrait être : un groupe de symétries. Le second est qu’il n’est la plupart du temps pas facile à calculer. Il faut pour cela développer des outils, décrits ailleurs, comme par exemple le théorème de Van Kampen.

La définition du groupe fondamental par les chemins

On se fixe un espace connexe par arcs $(B,b)$ pointé.

On note $\Omega(B,b)$ l’espace des lacets, muni de la topologie compacte ouverte.

On peut mettre « bout à bout » deux lacets pour en produire un troisième mais cela pose le problème de choisir un paramétrage, nécessairement de manière arbitraire. L’une des possibilités est la suivante.

Il faut prendre garde au fait que l’opération $\star$ ne jouit d’aucune propriété algébrique intéressante, et en particulier qu’elle n’est pas associative.

Le preuve est laissée en exercice et se réduit à quelques figures très simples.

La preuve est aussi un exercice facile ; elle est présentée sous forme d’animation ici.

Ainsi l’ensemble des classes d’homotopies à extrémités fixes de lacets de $\Omega(B,b)$ est également muni d’une opération $\star$ de concaténation.

Ce groupe est le groupe fondamental $\pi_1(B,b)$. Nous démontrerons plus loin que ce groupe coïncide en effet avec le groupe que nous avons introduit en termes de revêtements.

Démonstration. La démonstration du théorème n’est pas difficile et est présentée sous forme d’animations ici.

L’associativité de la concaténation à homotopie près se montre par la figure suivante.

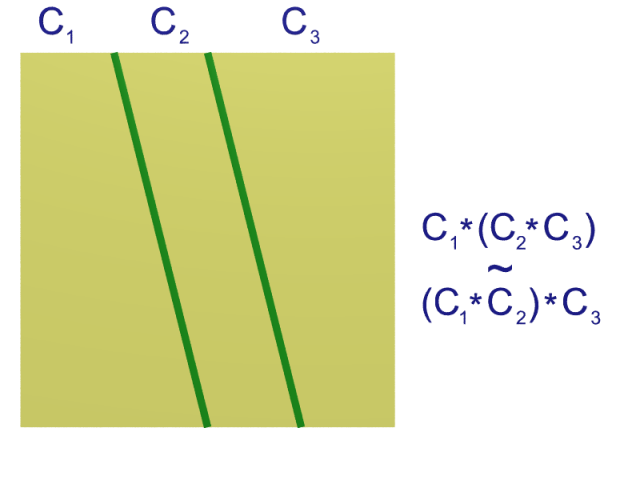
L’élément neutre est bien entendu le lacet constant. Le fait qu’il s’agit en effet d’un élément neutre est illustré par la figure suivante.

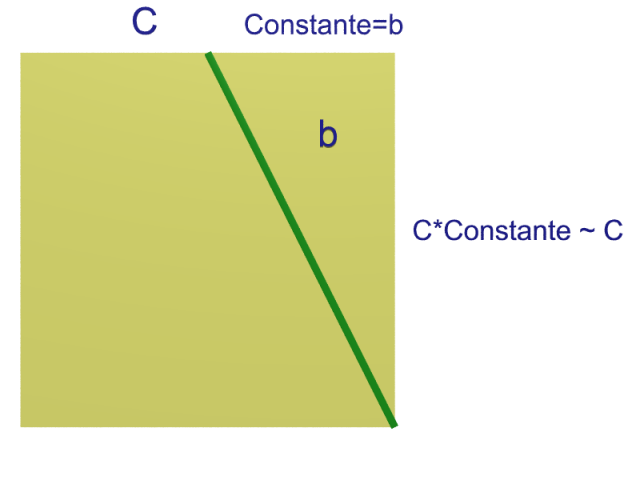
Enfin l’inverse d’un lacet $c$ est le lacet parcouru dans l’autre sens : $c^{-1}(t) = c(1-t)$. L’homotopie entre $c\star c^{-1}$ et le lacet constant est donnée par $H(s,t) = c(st)$ pour $0 \leq t \leq 1/2$ et $c(s(1-t))$ pour $1/2\leq t \leq 1$.

C.Q.F.D.

$$ $$

On peut maintenant passer aux choses sérieuses et démontrer que nos deux définitions du groupe fondamental sont équivalentes. On pourra sur ce sujet commencer par visionner le cours filmé ci-dessous qui commence par reprendre ce qui vient d’être dit.

L’identification entre les deux définitions du groupe fondamental

Dans ce paragraphe, nous allons montrer que les deux définitions du groupe fondamental, par les revêtements et par les lacets, sont équivalentes. Provisoirement, nous notons $\pi_1^{rev}(B,b)$ le groupe défini par les revêtements, et $\pi_1^{lac}(B,b)$ celui qui est défini par les classes d’homotopie de lacets.

Nous allons d’abord construire une application naturelle de $\Omega(B,b)$ vers $\pi_1^{rev}(B,b)$. Dans un second temps, nous montrerons que cette application passe au quotient en une application $\pi_1^{lac}(B,b) \to \pi_1^{rev}(B,b)$. Finalement, nous montrerons que cette application est un isomorphisme.

Soit $c$ un élément de $\Omega(B,b)$, i.e. une application continue $c: [0,1] \to B$ telle que $c(0)=c(1)=b$. Soit $\tilde{p} : (\tilde{B},\tilde{b}) \to (B,b)$ un revêtement universel de $(B,b)$.

L’image réciproque de $\tilde{p}$ par $c$ est un revêtement au dessus de $[0,1]$, donc trivial. Il existe donc une application $\tilde{c} : [0,1] \to \tilde{B} $ telle que $c = \tilde{p} \circ \tilde{c}$ et $\tilde{c} (0) = \tilde{b}$. Le relevé $\tilde{c}$ est un chemin mais n’est pas nécessairement un lacet. L’extrémité $\tilde{c}(1)$ est un point de $\tilde{B}$ dont la projection par $\tilde{p}$ est le point $b$. Il existe dont un unique élément $\gamma$ du groupe $\pi_1^{rev}(B,b)$ qui envoie $\tilde{b}$ sur $\tilde{c}(1)$. L’application $\Phi$ qui envoie $c \in \Omega(B,b)$ sur $\gamma \in \pi_1^{rev}(B,b)$ est celle qui va établir l’isomorphisme cherché entre $\pi_1^{lac}(B,b)$ et $\pi_1^{rev}(B,b)$.

La plupart des propriétés de $\Phi$ se vérifient facilement.

La première suit directement des définitions. L’application $\Phi$ envoie la concaténation de $c_1$ et $c_2$ sur la composition de $\Phi(c_1)$ et $\Phi(c_2)$. En effet, soit $\tilde{c_1}$ et $\tilde{c_2}$ les relevés de $c_1$ et $c_2$ tels que $\tilde{c_i} (0) = \tilde{b}$. Alors on a par définition $\Phi (c_1) \tilde{b} = \tilde{c_1} (1)$, et donc on peut considérer la concaténation $\tilde{c_1} \star (\Phi(c_1) \tilde{c_2})$. Il s’agit d’un relevé de $c_1\star c_2$, qui aboutit au point $\Phi(c_1) \tilde{c_2}(1)= \Phi (c_1) \Phi(c_2) \tilde{b}$, ce qui montre bien que $\Phi(c_1 \star c_2) = \Phi (c_1) \Phi(c_2)$.

Il s’agit ensuite de vérifier que deux lacets $c_1,c_2$ homotopes à extrémités fixes ont la même image par $\Phi$. Considérons pour cela une homotopie $H : [0,1]\times [0,1] \to B$. L’image réciproque du revêtement universel $\tilde{p}$ par $H$ est un revêtement trivial au dessus de $[0,1]\times [0,1]$. On dispose donc d’une application $\tilde{H} : [0,1]\times [0,1] \to \tilde{B}$ telle que :

• $\tilde{p} \circ \tilde{H} = H$
• $\tilde{H}(0,0) = \tilde{b}$.

Les chemins $\tilde{H}(s,0)$ et $\tilde{H}(s,1)$ se projettent dans $B$ sur un chemin constant égal à $b$. Ce sont donc des chemins constants dans $\tilde{B}$. On a bien sûr $\tilde{H}(s,0)= \tilde{b}$. Le point $\tilde{H}(s,1)$ quant à lui est un certain point de la fibre $\tilde{p}^{-1}(b)$, indépendant de $s$. Par définition, $\Phi(c_1)$ et $\Phi(c_2)$ sont les éléments de $\pi_1^{rev}(B,b)$ qui envoient $\tilde{b}$ sur $\tilde{H}(0,1)$ et $\tilde{H}(1,1)$ respectivement. On a donc $\Phi(c_1) = \Phi(c_2)$ comme annoncé.

Ainsi, nous avons construit un homomorphisme $\phi : \pi_1^{lac}(B,b) \to \pi_1^{rev} (B,b)$ et il nous reste à montrer qu’il s’agit d’un isomorphisme.

La surjectivité n’est pas difficile. Partant d’un élément $\gamma$ de $\pi_1^{rev}(B,b)$, on considère un chemin joignant $\tilde{b}$ à $\gamma(\tilde{b})$ dans $\tilde{B}$. Ce chemin se projette sur un lacet de $(B,b)$ sont l’image par $\phi$ est évidemment $\gamma$.

L’injectivité est un peu plus difficile.

Dans le cas le plus simple, nous devons montrer que les deux conditions suivantes sont équivalentes :

• Le groupe $\pi_1^{rev}(B,b)$ est trivial, i.e. $B$ est simplement connexe, dans le sens que tout revêtement connexe est trivial.
• Le groupe $\pi_1^{lac}(B,b)$ est trivial, i.e. $B$ est simplement connexe au sens des lacets : tout lacet de $(B,b)$ est homotope à extrémités fixes au lacet constant.

Pour cela nous devons construire des revêtements en termes de chemins et de lacets. On note $Ch(B,b)$ l’espace des chemins $c : [0,1] \to B $ tels que $c(0)=b$, muni de la topologie compacte ouverte. Deux chemins $c_1,c_2$ de mêmes extrémités sont homotopes à extrémités fixées s’il existe $H : [0,1]\times [0,1] \to B$ tel que

• $H(0,t) = c_1(t)$ pour tout $t \in [0,1]$,
• $H(1,t)= c_2(t)$ pour tout $t \in [0,1]$,
• $H(s,0)=b $ pour tout $s \in [0,1]$.
• $H(s,1)=H(0,1) $ pour tout $s \in [0,1]$.

On note $Ch_0(B,b)$ l’espace topologique quotient de $Ch(B,b)$ par la relation d’homotopie à extrémités fixes des chemins. L’espace $Ch_0(B,b)$ se projette sur $B$ par une application $p$ envoyant un chemin sur son extrémité $c(1) \in B$.

A priori, cet espace $Ch_0(B,b)$ peut-être très singulier, en particulier non séparé. Cependant, nous allons voir que lorsque $B$ ne présente pas de pathologies locales, et notamment si $B$ est une variété, alors $Ch_0(B,b)$ est séparé, et que $p$ est un revêtement.

Nous dirons que $B$ est localement connexe si tout point admet un voisinage connexe, et qu’il est localement compressible si tout point admet un voisinage dans lequel tout lacet peut être homotopé à un chemin constant, l’homotopie pouvant éventuellement prendre des valeurs en dehors du voisinage considéré.

Notons que la fibre au dessus du point $b$ est par définition $\pi_1^{lac}(B,b)$.

Démonstration de la proposition. Montrons d’abord que l’espace $Ch_0(B,b)$ est séparé. Pour cela il suffit de montrer que les classes d’équivalences d’homotopie à extrémités fixes dans $Ch(B,b)$ sont fermées. En fait nous allons montrer que tout chemin $c'\in Ch(B,b)$ qui a les mêmes extrémités qu’un chemin $c\in Ch(B,b)$ et qui est suffisamment proche de ce dernier lui est homotope à extrémités fixes.

L’argument dans le cas où $B$ est une variété lisse est très clair. En choisissant une métrique riemannienne sur $B$, pour chaque point $z$ de $B$ il existe un voisinage $U_z$ de $z$ tel que tout point de $U_z$ peut être joint à, $z$ par un unique arc géodésique de longueur minimale. Il suffit alors de joindre $c(t)$ et $c’(t)$ par l’unique arc géodésique minimal qui les joint pour trouver l’homotopie souhaitée.

Dans le cas général, on utilise la connexité locale afin de supposer que $c$ et $c'$ coïncident sur une subdivision $0<1/n<2/n<...<1-1/n<1$ assez fine de $[0,1]$, puis on utilise la compressibilité locale pour homotoper $c$ et $c'$ sur chaque intervalle $[k/n,k+1/n]$ en laissant les extrémités fixées. On laisse les détails au lecteur.

Nous avons donc montré que $Ch_0(B,b)$ est séparé. Nous allons maintenant voir que l’application $p:Ch_0(B,b) \rightarrow B$ est un revêtement.

Pour cela, nous devons construire les piles d’assiettes. Prenons un point $x\in B$, et choisissons un voisinage $U$ de $x$ qui est connexe par arc et compressible dans $B$. Pour toute classe $[c]\in p^{-1} (x)$, considérons la section $\sigma_{[c]} : U \rightarrow Ch_0(B,b)$ qui a un point $y\in U$ associe la classe d’homotopie du chemin $c \star [x,y]$, où $[x,y]$ est un chemin de $U$ liant $x$ à $y$. Comme $U$ est compressible dans $B$, cette définition ne dépend pas du choix du chemin $[x,y]$. Nous laissons au lecteur le soin de vérifier que les sections $\sigma_{[c]}$ sont continues, ouvertes, et d’images disjointes, ce qui sont exactement les propriétés requises pour que $p$ soit un revêtement.

C.Q.F.D.

$$ $$

Revenons à l’identification entre les groupes $\pi_1^{rev}(B,b)$ et $\pi_1^{lac}(B,b)$, en commençant par le cas où l’un des deux groupes est trivial.

Si $\pi_1^{rev}(B,b)$ est trivial, alors tout revêtement connexe de $B$ est trivial. En particulier, le revêtement $p:Ch_0(B,b)\to (B,b)$ est trivial, et sa fibre au dessus de $b$ ne contient qu’un élément, si bien que $\pi_1^{lac}(B,b)=0$.

Réciproquement, supposons que $\pi_1^{lac}(B,b)$ soit trivial. Si $B$ n’était pas trivial au sens des revêtements, cela signifierait que son revêtement universel $\tilde{p} : (\tilde{B},\tilde{b}) \to (B,b)$ n’est pas trivial. En joignant $\tilde{b}$ à un autre point de la fibre $\tilde{p}^{-1}(b)$, et en projettant dans $B$, on obtiendrait un lacet de $(B,b)$ qui ne se relèverait pas en un lacet de $\tilde{B}$ et qui ne serait donc pas homotope à un lacet constant, à extrémités fixes, ce qui contredit $\pi_1^{lac}(B,b) = 0$.

Le cas général n’est qu’une simple généralisation de cet exemple. Si un lacet $c$ de $\pi_1^{lac}(B,b)$ a une image triviale dans $\pi_1^{rev}(B,b)$, cela signifie qu’il se relève en un lacet de $\tilde{B}$. Mais puisque $\pi_1^{rev}(\tilde{B},\tilde{b})=0$, on a aussi $\pi_1^{lac}(\tilde{B},\tilde{b})=0$ si bien que ce relevé est homotope au lacet constant dans $\tilde{B}$ à extrémités fixes, et en particulier, en projetant cette homotopie dans $B$, le lacet $c$ est homotope à un lacet constant dans $B$ si bien que $c$ est trivial dans $\pi_1^{lac}(B,b)$. Le morphisme $\phi : \pi_1^{lac}(B,b) \to \pi_1^{rev}(B,b)$ est injectif.

Par conséquent, $\phi$ est un isomorphisme.
C.Q.F.D.

$$ $$