Fonctions multiformes et groupe fondamental

Le texte et les vidéos de cet article sont complémentaires (et majoritairement indépendants). L’objectif est de présenter des objets fondamentaux à l’époque de Poincaré : les fonctions multiformes. Ces fonctions ne sont pas des fonctions au sens moderne car à un point peuvent être associées plusieurs valeurs. Elles permettent de mettre en lumière une des origines de la théorie des revêtements. L’article sur la genèse du groupe fondamental chez Poincaré développe les aspects historiques.
Nous allons ici présenter les liens entre fonctions multiformes, revêtements et groupe fondamental et surtout donner beaucoup d’exemples.

La première vidéo introduit les fonctions multiformes. Elle suit le même plan que ce texte.

La seconde vidéo [1] se concentre sur les intégrales elliptiques

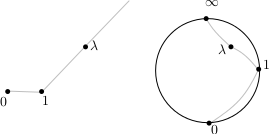
$$\int \frac{d x}{\sqrt{x(x-1)(x-\lambda)}}$$

où $\lambda \in\mathbb C\setminus\{0,1\}$ et décrit l’uniformisation du tore de $\mathbb C P^2$ associé à l’équation $y^2=x(x-1)(x-\lambda)$ ainsi que l’uniformisation de $\mathbb C\setminus \{0,1\}$ à l’aide de ces intégrales. Pour plus de détails sur l’uniformisation, on pourra consulter [2].

Fonctions multiformes

En général, les fonctions multiformes sont définies sur une surface de Riemann. Dans les exemples présentés ici, elle seront le plus souvent définies sur un domaine de $\mathbb C$.

Soit donc $S$ une surface de Riemann. Une fonction multiforme sur $S$ est une fonction holomorphe $f' : S'\to\mathbb C$ définie sur un revêtement $S'$ de $S$.

La fonction $f'$ ne permet usuellement pas de définir une fonction de $S$ dans $\mathbb C$ mais elle nous fournit des germes de fonctions en tout point de $S$. Ces germes peuvent être représentés par des fonctions définies sur un ouvert trivialisant du revêtement, il y en a au plus la cardinalité de la fibre.

Un des exemples les plus classiques de fonction multiforme est la racine carrée complexe : au voisinage de tout point de $\mathbb C^*$, il existe deux fonctions racine carré, qui sont l’opposé l’une de l’autre. Formellement, on considère le revêtement $\mathbb C^*\to\mathbb C^*$ donné par $z\mapsto z^2$ ainsi que l’application $\mathrm{Id} :\mathbb C^*\to\mathbb C^*$ comme application $f'$. On peut définir le logarithme complexe de façon analogue.

Une propriété fondamentale des fonctions multiformes est le prolongement le long des chemins ou prolongement analytique. Elle peut se formuler ainsi. Soit $c : [0,1]\to S$ un chemin et $g$ un germe de fonction holomorphe en $c(0)$. Le germe $g$ peut être prolongé analytiquement le long de $c$, s’il existe une subdivision $0=t_0\lt t_1\lt\dots\lt t_n$ de $[0,1]$, des disques $U_i\subset S$ centrés en $c(t_i)$ et des fonctions $f_i : U_i\to\mathbb C$ tels que

• le germe défini par $f_0$ en $c(0)$ est $g$
• les disques $U_i$ recouvrent l’image de $c$
• pour tout $i=0,\dots, n-1$, $U_i\cap U_{i+1}\neq\emptyset$ et $f_i=f_{i+1}$ sur $U_i\cap U_{i+1}$.

Voyons maintenant comment prolonger une fonction multiforme le long d’un chemin. Considérons donc une fonction multiforme sur $S$ définie par $f' : S'\to\mathbb C$ ainsi qu’un germe de fonction en un point $p$ de $S$ provenant de $f'$. Soit $c$ un chemin issu de $p$. Pour prolonger notre germe de fonction le long de $c$ :

• on considère un relevé $p'$ de $p$ tel que le germe de $f'$ en $p'$ soit notre germe de départ
• on relève $c$ en un chemin $c'$ issu de $p'$
• on prend comme germe le germe de $f'$ le long de $c'$.

Si le chemin $c$ est en fait un lacet, le prolongement le long de $c$ nous donne un nouveau germe en $p$. Ce germe ne dépend que de la classe d’homotopie de $c$. On parle de monodromie.

Réciproquement, tout germe de fonction défini sur une surface de Riemann vérifiant la propriété de prolongement le long des chemins donne naissance à une fonction multiforme : la propriété de prolongement le long de chemins permet en effet de définir une fonction sur le revêtement universel de notre surface de Riemann.

La fonction logarithme complexe est le plus souvent présentée grâce à cette propriété : on pose

$$\log(z)=\int_1^z \frac{d u}{u}$$

où l’intégrale est calculée le long d’un chemin de $\mathbb C^*$ reliant $1$ à $z$. Plus précisément, si $c : [0,1]\to\mathbb C^*$ est un tel chemin, on pose

$$\log(z)=\int_0^1 \frac{c'(t)}{c(t)}d t.$$

Fonctions multiformes et groupe fondamental

Considérons une fonction multiforme sur $S$ définie par $f' : S'\to \mathbb C$. Fixons un point $p$ de $S$ et considérons l’ensemble $G$ des germes de notre fonction multiforme en $p$. Notons $S(G)$ le groupe des permutations de $G$. À un élément de $\pi_1(S,p)$ on peut associer un élément de $S(G)$, on obtient ainsi un morphisme

$$\phi : \pi_1(S,p)\to S(G).$$

Ce morphisme n’est pas toujours injectif. C’est par exemple le cas, si $f'$ est défini sur un revêtement $S'$ qui n’est pas le revêtement universel de $S$.

Dans le cas de la racine carrée complexe, il existe deux germes au voisinage du point $1$ (ou de n’importe quel autre point non nul), on a donc $S(G)=\mathbb Z/2\mathbb Z$. Le groupe fondamental de $\mathbb C^*$ est $\mathbb Z$ et il est engendré par la classe du lacet $c :t\mapsto \exp(2i\pi )$. Le prolongement analytique le long de $c$ permute les germes de la racine carrée, ce qui se traduit par $\phi([c])=-1$.

Au voisinage de $1$, les germes du logarithme sont les différentes déterminations du logarithme soit $G=\mathrm{Log} + 2i\pi\mathbb Z$ où $\mathrm{Log}$ est la détermination principale du logarithme donnée, par exemple, par son développement en série entière au voisinage de $1$. Le prolongement analytique le long du lacet $c :t\mapsto \exp(2i\pi t)$ ajoute $2i\pi$ au germe considéré. Dans ce cas, $\phi$ est injective et le groupe fondamental de $\mathbb C^*$ est représenté dans $S(G)$ par les translations de $2ik\pi$ pour $k\in\mathbb Z$.

Passons maintenant à l’étude d’exemples de fonctions multiformes.

Exemple des fonctions algébriques

Soit $P\in \mathbb C[x,y]$ un polynôme irréductible et $d$ le degré de $P$ vu comme polynôme en $y$. Notons $F$ l’ensemble des points $x\in\mathbb C$ tels que le coefficient dominant de $P$ vu comme polynôme en $y$ s’annule ou que le système

$$\left\{\begin{array}{c} P(x,y)=0\\ \frac{\partial P}{\partial y}(x,y)=0 \end{array}\right.$$

ait une solution. Cet ensemble est fini. Les points $x$ satisfaisant la seconde conditions peuvent, par exemple, être déterminés en cherchant les racines du résultant en $y$ des polynômes $P$ et $\frac{\partial P}{\partial y}$ (le résultant est alors un élément de $\mathbb C[x]$). Considérons l’ouvert $S=\mathbb C\setminus F$.

Par définition de $F$, pour tout $x_0\in S$, l’équation $P(x_0,y)$ admet exactement $d$ solutions distinctes (ces solutions sont toutes de multiplicité $1$). On peut même dire mieux, sur $S$, l’équation $P(x,y)=0$ définit une fonction multiforme : si $x_0$ est un point de $S$, il existe un voisinage $V(x_0)$ de $x_0$ et $d$ fonctions holomorphes $g_i : V(x_0)\to\mathbb C$,$ i =1,\dots, d$ telles que $P(x,g_i(x))=0$ pour tout $x\in V(x_0)$. Notre fonction multiforme est ainsi définie de façon uniforme sur un revêtement $S'$ à $d$ feuillets de $S$. Voir [3] pour plus de détails.

Nous allons ici nous intéresser à deux exemples :

• $P(x,y)=y^2-x$
• $Q(x,y)=y^2-x(x-1)(x-\lambda)$ où $\lambda\in\mathbb C\setminus \{ 0,1\}$.

Le premier exemple nous donne une nouvelle façon de construire la fonction multiforme racine carrée. Le second exemple est également étudié dans la seconde vidéo.
On peut facilement vérifier que ces deux exemples sont définis sur un revêtement à deux feuillets de $\mathbb C\setminus\{0\}$.

Le revêtement de $S$ sur lequel est défini notre fonction multiforme n’est pas compact. Il existe un procédé général pour associer une surface de Riemann compacte à un polynôme irréductible $P\in \mathbb C[x,y]$ (voir [4]). Cette construction repose sur la description de la fonction multiforme au voisinage des points de $F$. Nous allons décrire cette surface et étudier sa topologie dans les exemples simples décrit ci-dessus.

Commençons par le cas $P(x,y)=y^2-x$. La première étape est d’homogénéiser $P$, on considère donc le polynôme $\overline{P}(x,y,z)=y^2-xz\in\mathbb C[x,y,z]$. L’équation $\overline{P}=0$ définit une surface lisse $\Sigma$ de $\mathbb CP^2$ (il suffit d’appliquer le théorème des fonctions implicites). On va montrer que $\Sigma$ est une sphère.

La fonction racine carrée est définie de façon uniforme sur la surface $S'=\Sigma\setminus\{[0:0:1],[0:1:0]\}$. C’est un revêtement à deux feuillets de $S=\mathbb C\setminus \{0\}$. Découpons $\mathbb C\setminus\{0\}$ le long de $\mathbb R_-$ (appelé coupure). On obtient alors une surface simplement connexe au dessus de laquelle notre revêtement à deux feuillets est trivial, c’est à dire composé de deux sphères de Riemann découpées le long d’un segment.

Les couleurs sur les bords de la coupure permettent de repérer les bords qui se correspondent.

Pour décrire $S'$ et $\Sigma$, il nous reste à décrire comment les bords de la coupure se recollent entre eux. La monodromie nous donne alors la marche à suivre :

• en dehors de $0$ et $\infty$ les points de la coupure sont des points de $S$ : $S'$ est donc un revêtement à deux feuillets au dessus de ces points, il nous faut donc recoller entre eux des segments de couleurs différentes
• la monodromie de la fonction racine carrée autour de l’origine permute les germes de racines, par conséquent, il faut associer les bords de coupures correspondant à des composantes connexes différentes.

On obtient donc bien une sphère !

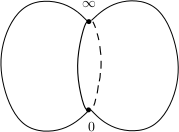
Voici par exemple un relevé du cercle unité.

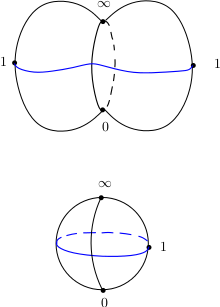
La surface $\Sigma$ est un revêtement ramifié au dessus de la sphère de Riemann.

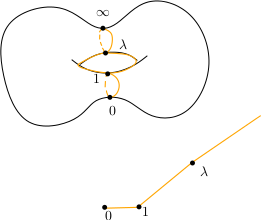
Passons maintenant au second exemple : $Q(x,y)=y^2-x(x-1)(x-\lambda)$ où $\lambda\in\mathbb C\setminus \{ 0,1\}$. On applique la même méthode, on commence donc par considérer le polynôme homogénéisé $\overline{Q}(x,y,z)=zy^2-x(x-z)(x-\lambda z)\in\mathbb C[x,y,z]$. L’équation $\overline{Q}=0$ définit encore une surface lisse $\Sigma$ de $\mathbb CP^2$. On va montrer que $\Sigma$ est un tore. Une autre preuve est présentée dans la seconde vidéo.

On choisit donc une coupure de $\mathbb C$ (ou plutôt de la sphère de Riemann) qui relie les points $0$, $1$, $\lambda$ et $\infty$ et on découpe le long de cette coupure.

Au dessus de $\mathbb C$ privé de la coupure, le revêtement est un revêtement trivial à deux feuillets et il nous reste à décrire comment recoller entre eux les bords de la coupure dans ce revêtement pour décrire $\Sigma$.

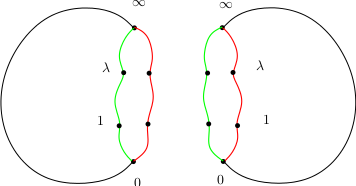
Sur la figure, les couleurs sur les bords de la coupure permettent de repérer les bords qui se correspondent. Comme dans le cas de la racine carrée, il faut recoller entre eux des segments de couleurs différentes en tenant compte de la monodromie. Au voisinage de $0$, $1$ ou $\lambda$, la monodromie peut se déduire de la monodromie de la racine carrée : quand on fait le tour d’une seule singularité, les germes associés à la fonction multiforme sont permutés. On obtient donc le dessin suivant et $\Sigma$ est bien un tore (la trace de la coupure est dessinée en orange).

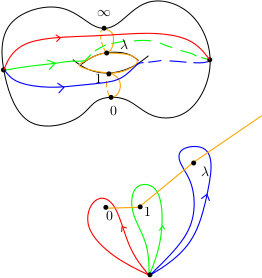
Voici des relevés des lacets engendrant le groupe fondamental de $S$.

Le cas général est plus délicat car la surface obtenue dans $\mathbb CP^2$ n’est pas toujours lisse (voir par exemple [5]).

Exemple des intégrales

Soit $S$ une surface de Riemann. On considère une fonction holomorphe $u : S\to \mathbb C$. La fonction $u$ n’admet pas toujours de primitive définie sur $S$, on peut par exemple penser à $u :z\mapsto \frac{1}{z}$ définie sur $S=\mathbb C^*$. Par contre une primitive existe localement et peut être prolongée le long des chemins. On obtient donc une fonction primitive multiforme, définie à ajout d’une constante près.
On peut, par exemple, définir ainsi les fonctions $\log$, $\arctan$... (Remarquons quand-même que la fonction $\arctan$ n’est pas vraiment un exemple nouveau car elle peut s’écrire comme somme de deux $\log$).

Un lacet $c$ de $S$ agit sur $\int u$ en ajoutant la constante $\int_c u$. L’action du groupe fondamental est donc toujours commutative dans le cas d’une primitive.

On peut bien sûr empiler les couches de multiformité en considérant des primitives de fonctions elles-mêmes multiformes. La seconde vidéo présente ainsi un exemple d’intégrale elliptique.

Une primitive de $u$ est une solution de l’équation différentielle $y'=u$. Plus généralement les solutions d’équations différentielles fournissent des exemples de fonctions multiformes.

Exemple des solutions d’équations différentielles

Les solutions d’une équation différentielle à coefficients holomorphes existent localement et peuvent être prolongées le long des chemins. Elles définissent donc des fonctions multiformes.

Équations linaires homogènes d’ordre 1

Au voisinage d’un point, l’espace des solutions est un espace vectoriel de dimensions $1$, on dispose même d’une description explicite des solutions. L’action d’un lacet sur l’espace des solutions est donc décrite par la donnée d’un nombre complexe non nul.

Par exemple, l’équation

$$2zy'=y.$$

a une singularité en $0$ et ses solutions sont les $z\mapsto \lambda\sqrt{z}$ pour $\lambda\in\mathbb C$. Le lacet $t\mapsto e^{2i\pi t}$ agit sur les solutions au voisinage de $1$ par multiplication par $-1$.

Équations linaires homogènes d’ordre 2

Localement, l’espace des solutions est de dimension $2$, il est donc décrit par une base de solutions $(w_1,w_2)$. En prolongeant la base $(w_1,w_2)$ le long d’un lacet, on obtient une nouvelle base de solutions. Elle s’écrit $M(w_1,w_2)$ où $M\in\mathrm{GL}_2(\mathbb C)$. L’action du groupe fondamental est donc décrite par une matrice de $\mathrm{GL}_2(\mathbb C)$.

Considérons l’équation

$$4z^2y''+2y'+y=0.$$

Elle possède une singularité en $0$ et une base de solutions est $\left(\cos(\sqrt{z}),\sin(\sqrt{z})\right)$. Le lacet $t\mapsto e^{2i\pi t}$ agit sur cette base en la transformant en la base $\left(\cos(\sqrt{z}),-\sin(\sqrt{z})\right)$. L’action de $\mathbb Z$ (le groupe fondamental de $\mathbb C^*$) est donc décrite par la matrice

$$\left(\begin{array}{cc} 1&0\\ 0&-1 \end{array}\right)$$

L’équation

$$4z^2y''+y=0$$

nous fournit une monodromie plus compliquée. En effet, une base de solution est $\left(\sqrt{z},\sqrt{z}\log(z)\right)$. Le lacet $t\mapsto e^{2i\pi t}$ agit sur cette base en la transformant en $\left(-(1+2i\pi)\sqrt{z},-\sqrt{z}\log(z)\right)$. L’action de $\mathbb Z$ est alors décrite par la matrice

$$\left(\begin{array}{cc} -1&2i\pi\\ 0&-1 \end{array}\right)$$

Pour en savoir plus sur les équations différentielles, on pourra consulter [6] ou [7].