|
> Exemples de dimension 3 > Recollements du cube > La variété hypercubique La variété hypercubiqueTroisième exemple de recollement du cube |
L’exemple 3 de Poincaré illustre à merveille la confrontation entre deux points de vue sur le groupe fondamental. Le premier consiste à déterminer le groupe fondamental d’une variété « à la Van Kampen » et d’arriver ainsi à une présentation du groupe par générateurs et relations. Le deuxième point de vue — qui est plutôt le premier point de vue de Poincaré sur le groupe fondamental — consiste à identifier la variété comme un quotient de son revêtement universel (à déterminer) par un groupe cette fois explicite. [1] Commençons par décrire l’espace à étudier.
Une variété de dimension $3$
On construit un espace topologique $V$ en recollant chaque face du cube $C=[-1,1]^3$ à la face opposée via un vissage d’un quart de tour dans le sens direct. Plus précisément, on identifie
- le point $(-1, y, z)$ de la face gauche avec le point $(1, -z, y)$ de la face droite ;
- le point $(x, -1, z)$ de la face avant avec le point $(z, 1, -x)$ de la face arrière ;
- le point $(x, y, -1)$ de la face inférieure avec le point $(-y, x, 1)$ de la face supérieure.
Ce recollement correspond à l’espace $K_{\pi/2,\pi/2,\pi/2}$ décrit dans la présentation générale des recollements du cube. La première identification est matérialisée dans l’animation ci-dessous.
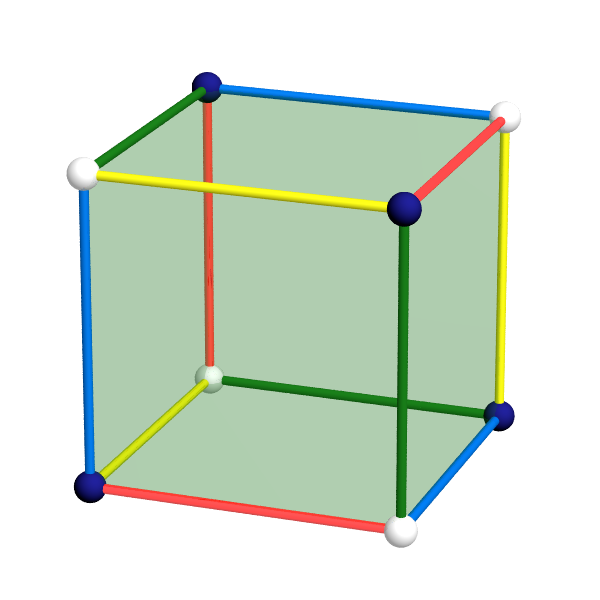
On observe alors que les douze arêtes du cube sont identifiées trois par trois et que les sommets sont identifiés quatre par quatre, comme dans l’animation ci-dessous.
$V$ est une variété
On dénombre quatre classes de trois arêtes et deux classes de quatre sommets, ce que résume la figure ci-dessous.
La caractéristique d’Euler de $V$ est donc $2- 4+ 3- 1=0$, et le critère de Poincaré montre que $V$ est une variété.
Vérifions ce résultat « à la main » : les points de $V$ se séparent en effet en quatre catégories :
- les images de points de l’intérieur de $C$ ;
- les images de points appartenant à l’intérieur des faces de $C$ ;
- les images de points appartenant à l’intérieur des arêtes de $C$ ;
- les images des sommets de $C$.
Remarquons que les identifications des faces envoient bien arête sur arête et sommet sur sommet, donc cette disjonction de cas est légitime. La situation serait plus compliquée si, par exemple, un point de l’intérieur d’une face pouvait être identifié avec un sommet d’une autre face.
Nous allons maintenant montrer que dans chacun de ces quatre cas, le point admet (dans $V$) un voisinage homéomorphe à une boule, ce qui montrera que $V$ est une variété. Comme on va le voir, seul le dernier cas utilise les particularités des identifications que nous venons de donner. Autrement dit, si l’on recolle les faces d’un cube par des identifications entre faces opposées, seuls les sommets pourraient empêcher l’espace topologique ainsi créé d’être une variété.
$$ $$
Points intérieurs. Puisque les identifications ne concernent que les faces de $C$, si $q \in C$ est un point intérieur, il est le seul antécédent de son image $[q]$ dans $V$ et la projection $\pi: C \to V$ est un homéomorphisme au voisinage de $q$. Si $q \in B \subset C$ est une boule suffisamment petite, $\pi (B) \subset V$ sera un voisinage de $p$ homéomorphe à une boule.
$$ $$
Points sur les faces. Soit $F$ une des six faces du cube et $q \in F$. Par construction, on identifie le point $q$ de $F$ à son image $f(q)$ dans la face opposée $F'$ par la translation/rotation $f : F \to F'$. Les antécédents de $[q]$ sont exactement $q \in F$ et $f(q) \in F'$. Dans $C$, chacun de ces deux points a un voisinage homéomorphe à une demi-boule, et l’on peut choisir ces deux demi-boules $B$ et $B'$ de telle sorte que $\pi (B) \cup \pi (B')$, qui est un voisinage de $[q]$, soit homéomorphe à une boule.
$$ $$
Points sur les arêtes. Puisque chaque arête est identifiée avec deux des onze autres arêtes du cube, l’image dans $V$ des intérieurs des arêtes est formée des points $[q_1] = [q_2] = [q_3]$, où les $q_i$ sont des éléments d’une classe d’arête $\{a_1, a_2, a_3\}$ se correspondant par les diverses identifications.
Dans $C$, chacun des $q_i$ a un voisinage homéomorphe à $S \times \ell_i$, où $S$ est un secteur angulaire d’angle $\pi/2$ et $\ell_i \subset a_i$ est un petit arc. On peut choisir ces voisinages de telle sorte que les arcs $\ell_i$ soient images les uns des autres par les identifications et que les secteurs angulaires se rassemblent pour former un disque comme dans l’animation suivante.
On obtient ainsi un voisinage du point $[q_i] \in V$ homéomorphe au produit d’un disque et d’un arc, c’est-à-dire à une boule.
Remarquons que le nombre d’antécédents différents (ici, $3$) ne joue pas de rôle. Comme $n$ secteurs angulaires s’assemblent toujours pour former un disque, l’argument que l’on vient de donner est en fait général.
$$ $$
Sommets. On a vu que les huit sommets du cube se répartissaient en deux classes de quatre sommets. Dans $C$, chacun des sommets a un voisinage homéomorphe à un huitième de sphère, ce que l’on peut voir comme un cône à base triangulaire. Encore une fois, on peut choisir ces voisinages de telle sorte qu’ils se recollent parfaitement les uns aux autres. Autrement dit, si $q_1, q_2, q_3$ et $q_4$ sont les quatre sommets d’une même classe, on peut choisir les voisinages de telle sorte que les quatre bases triangulaires $T_1, T_2, T_3$ et $T_4$ se recollent pour former une surface triangulée $L$. Le point $[q_i]$ possède alors un voisinage homéomorphe au cône de base $L$.
En général, il n’y a aucune raison pour que la surface $L$ soit homéomorphe à une sphère et donc pour que le voisinage soit une boule (voir par exemple, l’exemple 2). Dans le cas que nous considérons, les quatre triangles s’assemblent selon le même agencement que les quatre faces d’un tétraèdre, comme le montre l’animation ci-dessous.
Présentation du groupe fondamental
Déterminons une présentation de son groupe fondamental en utilisant la méthode de Poincaré. En conservant les notations introduites pour le recollement général d’une cube, les cycles d’arêtes sont les suivants :
$$(Z^+\cap X^+ ,X^- \cap Y^+,Y^-\cap Z^-) \quad (Z^-\cap X^- ,X^+ \cap Y^+,Y^-\cap Z^+)$$
$$(Z^+\cap Y^+, Y^-\cap X^-,X^+\cap Z^- )\quad (Y^-\cap X^+,X^-\cap Z^+,Z^-\cap Y^+)$$
À chacun correspond une relation liant les générateurs $I$, $J$, $K$ du groupe fondamental de la variété :
$$IJ K^{-1} = 1,\quad I^{-1}JK=1,\quad JI^{-1}K^{-1} =1,\quad IKJ=1.$$
L’animation suivante permet de visualiser la première de ces relations.
On obtient que
$$\pi_1(V)=\langle I,J,K \; | \; IJ=K, JK = I, KI=J; IKJ=1\rangle$$
On reconnaît là une présentation du groupe de quaternions
$$Q_8=\{\pm1,\pm i, \pm j,\pm k\}\subset \mathbb{H}^\times.$$
On pourra voir les détails du raisonnement dans le bloc Envie de voir les calculs ? de notre Commentaire du §13).
Le groupe de quaternions $Q_8$ et l’hypercube
Nous allons voir que l’on peut en fait obtenir la variété $V$ comme quotient de la sphère $\mathbb{S}^3$ par une action libre de $Q_8$, ce qui démontrera a fortiori l’isomorphisme $\pi_1(V) \simeq Q_8$, sans utiliser le théorème du domaine fondamental ou le théorème de Van Kampen.
L’action du groupe $Q_8$ par multiplication à gauche sur le le corps des quaternions $\mathbb{H}$ préserve l’hypercube unité
$$H = [-1, 1]^4 =\{t + x i + yj + zk \; | \; -1 \leq t, x, y, z\leq 1\} \subset \mathbb{H}.$$
En particulier, elle induit une action sur le bord $\partial H$ de cet hypercube, qui est combinatoirement constitué de $8$ cubes (et $24$ faces carrées, $32$ arêtes et $16$ sommets) et est homéomorphe à la sphère $\mathbb{S}^3$. Chacun de ces cubes est centré en l’un des quaternions $q \in Q_8$. On notera $C_q$ le cube centré en $q$. Par exemple,
$$C_{-i} = \{ t - i + yj + zk \; | \; -1\leq t, y, z \leq 1\}$$
$$C_1 = \{1 + xi + yj + zk \; | \; -1 \leq x, y, z \leq 1\}.$$
Dans la suite, on identifiera ce dernier cube au cube unité $C = [-1, 1]^3 \subset \mathbb{R}^3$.
Comme restriction de l’action par multiplication à gauche de $\mathbb{H}^\times$ sur lui-même, l’action de $Q_8$ sur $\mathbb{S}^3$ est évidemment libre. En particulier, le quotient $Q_8 \backslash \mathbb{S}^3$ est une variété et la surjection canonique $\mathbb{S}^3 \to Q_8\backslash \mathbb{S}^3$ en est le revêtement universel. Nous allons démontrer que $Q_8 \backslash \mathbb{S}^3$ s’identifie à la variété $V$.
$$ $$
Si $q$ et $q'$ sont des éléments de $Q_8$, $q$ envoie le cube $C_{q'}$ sur $C_{qq'}$. Le fait que l’action par multiplication à gauche de $Q_8$ sur lui-même soit simplement transitive entraîne donc que tout élément $p \in\mathbb{S}^3$ est dans l’orbite d’un élément de $C_1 = C$ et que cet élément est même unique sauf si $p$ appartient à plusieurs cubes $C_q$, c’est-à-dire sauf s’il est situé à la frontière d’un de ces cubes. Autrement dit, le cube de référence $C_1$ est un domaine fondamental de l’action.
L’animation ci-dessous — obtenue par projection stéréographique de la projection radiale de $\partial H$ sur $\mathbb{S}^3$ — montre l’orbite d’un élément non trivial de $Q_8$ sur l’ensemble des arêtes de $H$. Le cube $C_1$ est identifié au cube intérieur de la figure.
Le quotient $Q_8 \backslash \mathbb{S}^3$ peut donc être obtenu comme un quotient de $C$ décrit par des identifications des différentes faces de $\partial C$. Plus précisément,
- la multiplication par $i$ identifie la face de gauche $C_1 \cap C_{-i}$ à la face de droite $C_i \cap C_1$ via
$$ 1 - i + yj + zk \mapsto 1 + i - zj + yk,$$
- la multiplication par $j$ identifie la face de devant $C_1 \cap C_{-j}$ à la face de derrière $C_j \cap C_1$ via
$$1 + xi - j + zk \mapsto 1 + zi + j -xk,$$
- la multiplication par $k$ identifie la face du bas $C_1 \cap C_{-k}$ à la face du haut $C_k \cap C_1$ via
$$1 + xi + yj - k \mapsto 1 - yi + xj + k$$
- la multiplication par $-i$ identifie la face de droite à la face de gauche par l’identification réciproque de celle donnée à la première ligne (et il se passe la même chose, mutatis mutandis, pour les multiplications par $-j$ et $-k$) ;
- la multiplication par $-1$ envoie $C_1$ sur le cube $C_{-1}$ qui est disjoint de $C_1$. Elle ne donne donc lieu à aucune identification.
En résumé, l’inclusion $C \subset \mathbb{S}^3$ induit un homéomorphisme entre le quotient $Q_8 \backslash \mathbb{S}^3$ et la variété $V$ obtenue par identification des faces de $C$.
La sphère d’homologie que Poincaré construit dans le cinquième complément est homéomorphe à la variété dodécaédrique que l’on peut de manière similaire obtenir comme quotient de $\mathbb{S}^3$ par un autre sous-groupe fini de quaternions, le groupe des icosions qui a 120 éléments.
[1] Notons qu’il existe beaucoup de présentations par générateurs et relations du groupe trivial ! Poincaré ne cache donc pas sa préférence pour le second point de vue.