Un recollement qui n’est pas une variété

On construit un espace topologique $V$ qui n’est pas une variété en recollant chaque face de $[-1,1]^3$ à la face opposée via un vissage d’un quart de tour direct dans un cas, indirect dans les deux autres, comme dans l’exemple 2 de Poincaré. Plus précisément, on identifie :

• le point $(-1, y, z)$ de la face gauche avec le point $(1, -z, y)$ de la face droite ;
• le point $(x, -1, z)$ de la face avant avec le point $(-z, 1, x)$ de la face arrière ;
• le point $(x, y, -1)$ de la face inférieure avec le point $(y, -x, 1)$ de la face supérieure.

Cet exemple correspond à l’espace $K_{\pi/2,-\pi/2,-\pi/2}$ décrit dans la présentation générale des recollements du cube.

On dénombre deux classes de six arêtes et deux classes de quatre sommets représentés sur la figure.

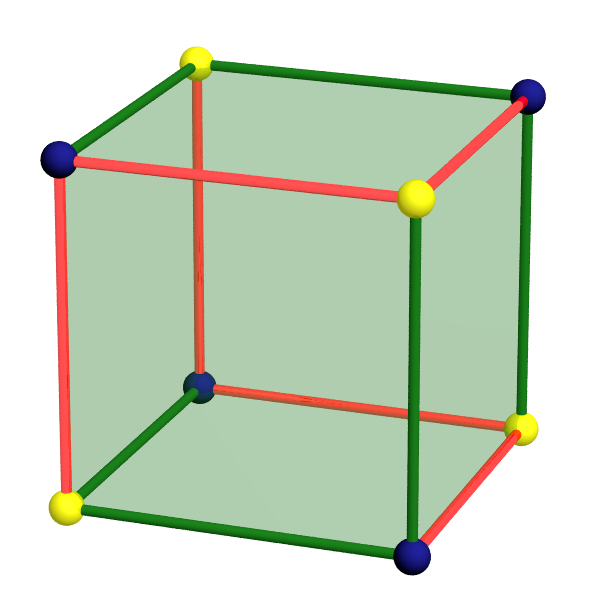
La caractéristique d’Euler du quotient est donc $2-2+3-1=2\neq0$. Il ne s’agit donc pas d’une variété d’après le critère décrit ici.

Afin de mieux comprendre cet espace, décrivons le link $L_p$ d’un sommet $p$. Pour cela, calculons sa caractéristique d’Euler. On obtient une décomposition cellulaire du link en coupant et recollant les coins du cube qui se projettent sur $p$. L’animation nous montre que le link cherché est un tore.

Le nombre de faces du link $L_p$ de $p$ dans $V$ est $4$, le nombre de sommets du cube ayant $p$ pour image dans $V$. Chacun de ces sommets est de valence $3$ dans le cube et les faces sont identifiées deux-à-deux donc le nombre d’arêtes de $L_p$ est $6$. Enfin le nombre de sommets de $L_p$ est le nombre de classes d’arêtes contenant l’un des antécédents de $p$, soit $2$. Ainsi,

$$\chi(L_p)=4-6+2=0$$

donc $L_p$ est un tore, puisque c’est une surface fermée orientable.