Les variétés de dimension $2$, ou surfaces, surgissent naturellement dans diverses branches des mathématiques allant de l’analyse complexe aux systèmes dynamiques, en passant par la géométrie algébrique qui les a vues naître.
Une des raisons pour lesquelles les surfaces sont un objet si souvent étudié est qu’on est capable d’en dresser une classification complète, du moins pour les surfaces fermées, c’est-à-dire compactes sans bord. Möbius fut le premier à s’attaquer au problème de la classification des surfaces. Dans un article de 1863 [1], il classifie les surfaces plongées de façon lisse dans l’espace euclidien de dimension 3. Il s’agit toujours de surfaces orientables. Quant aux surfaces non orientables, les premiers résultats furent annoncés par von Dyck en 1888 mais la preuve s’est avérée incomplète. Il est à noter qu’à cette époque, le concept de surface abstraite non plongée dans un espace euclidien n’avait pas encore été dégagé... [2]
Cette classification est donc antérieure à l’Analysis Situs. Une des motivations des travaux de Poincaré est d’ailleurs de généraliser certaines notions déjà connues pour les surfaces (comme la caractéristique d’Euler ou l’ « ordre de connexion ») aux variétés de dimension supérieure. Mais ses travaux apportent aussi un regard nouveau sur les surfaces et en permettent in fine une meilleure compréhension.
Dans cette rubrique, nous décrivons donc la topologie des surfaces sous de multiples points de vue, ce qui nous permettra d’aborder de nombreuses notions de topologie algébrique dans un cadre relativement simple, mais qui se révèle déjà d’une grande richesse.
Avant les surfaces : les courbes
Avant de s’intéresser aux variétés de dimension $2$, il peut être utile de commencer par décrire les variétés de dimension $1$, ou courbes. C’est facile : à homéomorphisme près, il n’y a que deux variétés connexes (sans bord) de dimension $1$ : le cercle et la droite.

- Un cercle et une droite. (À homéomorphisme près bien sûr !)
Quelques surfaces en images
Pour se familiariser avec les surfaces, on commencera par décrire sous plusieurs aspects quelques surfaces usuelles. Dans un premier article, on présente la sphère, le cylindre et le tore.
- Les premières surfaces : la sphère, le cylindre, le tore.

- Dans l’ordre : une sphère, un cylindre et un tore.

- Une bouteille de Klein immergée — mais pas plongée — dans l’espace.
Dans un second article, on introduit les surfaces non-orientables, en commençant par le ruban de Möbius, puis en continuant avec le plan projectif et la bouteille de Klein, dont on visualisera quelques représentations dans l’espace.
Notons que ces représentations sont nécessairement imparfaites. En effet, il est impossible de plonger une surface fermée non-orientable dans l’espace. La preuve de ce fait n’est pas simple et demande déjà quelques connaissances en théorie de l’homologie. Elle fait l’objet de l’article :
Vers une classification des surfaces fermées
La deuxième partie de cette rubrique conduit à une classification des surfaces fermées. On commence par introduire une « opération » sur les surfaces appelée somme connexe. Cette, opération, très visuelle, permet de construire des surfaces plus compliquées que celles que nous avons vu jusqu’ici. En faisant la somme connexe de $g$ tores, on obtient une surface qu’on appellera surface de genre $g$.
- Somme connexe, surface de genre $g$.

- La somme connexe de trois tores donne une surface de genre $3$.
On définit ensuite la caractéristique d’Euler d’une surface, un invariant topologique qui nous permet de montrer que les surfaces ainsi construites sont distinctes. Cet invariant se calcule à partir d’une décomposition polyédrale de la surface (c’est-à-dire d’une décomposition en sommets, arêtes et faces), mais le résultat est en fait indépendant de cette décomposition. Comme la caractéristique d’Euler de la surface de genre $g$ est égale à $2g-2$, les surfaces de genre $g_1$ et $g_2$ ne sont homéomorphes que si $g_1 = g_2$.
On peut enfin s’attaquer au théorème de classification des surfaces fermées :
- la somme connexe de $g$ tores si la surface est orientable,
- la somme connexe de $g$ plans projectifs si la surface est non-orientable.
En particulier, la caractéristique d’Euler classifie les surfaces fermées orientables.
Nous présentons trois démonstrations différentes de ce théorème. La première démonstration (uniquement pour les surfaces orientables) consiste à montrer que toute surface fermée orientable autre que la sphère peut être obtenue en recollant de façon bien précise les côtés d’un polygone à $4g$ côtés (voir figure ci-dessous). On reconnaît dans ce recollement la surface de genre $g$.
- Classification des surfaces triangulées par réduction à une forme normale.
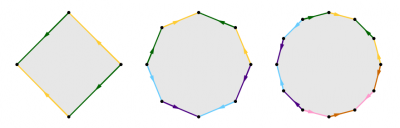
- Si on recolle les côtés de même couleur de ces polygones en suivant l’orientation indiquée par les flèches, on obtient (dans l’ordre) un tore, une surface de genre $2$ et une surface de genre $3$.
Une deuxième démonstration consiste à prouver que toute surface fermée est homéomorphe à une sphère à laquelle on a ajouté des « protubérances » appelées anses et calottes croisées. On montre ensuite qu’en présence de calottes croisées, on peut faire « disparaître » les anses. On obtient en définitive que toute surface fermée est soit une sphère avec $g$ anses (on reconnaît alors la surface de genre $g$), soit une sphère avec $g$ calottes croisées (dans laquelle on reconnaît la somme connexe de $g$ plans projectifs).
Ces deux démonstrations reposent sur l’existence d’une triangulation de la surface considérée. L’existence d’une telle triangulation fait l’objet de la rubrique Triangulation des variétés dans le cours moderne.
Pour finir, la troisième preuve, sous forme de cours filmé, utilise la théorie de Morse. Elle constitue une très bonne introduction à cette théorie, qui est développée plus largement dans le cours moderne.
Groupe fondamental et homologie des surfaces
Dans l’Analysis Situs, Poincaré construit deux nouveaux types d’invariants topologiques des variétés, leur groupe fondamental et leurs groupes d’homologie. Maintenant que nous savons décrire toutes les surfaces, nous pouvons tenter de calculer ces invariants topologiques.
Pour comprendre le groupe fondamental d’une surface, un point de vue consiste à « déplier » la surface pour obtenir une variété simplement connexe : le revêtement universel de la surface. La surface s’identifie alors au quotient de son revêtement universel par un groupe de transformations qui est précisément son groupe fondamental. Cette approche du groupe fondamental via le revêtement universel — sorte de « montée vers l’absolu » que sécrète toute variété (selon le philosophe Albert Lautman) — est développée dans la rubrique "Groupe fondamental par les revêtements". Nous illustrons cette idée dans le cas des surfaces dans l’article :
Pour aller plus loin dans cette direction, on pourra ensuite se pencher sur les revêtements ramifiés entre surfaces.
La connaissance des groupes d’homologie d’une surface $\Sigma$ en degré $0$ et $2$ n’apporte pas beaucoup d’information : si $\Sigma$ est connexe, alors $H_0(\Sigma,\mathbb{Z})$ est isomorphe à $\mathbb{Z}$, tandis que $H_2(\Sigma,\mathbb{Z})$ est isomorphe à $\mathbb{Z}$ si $\Sigma$ est fermée et orientable, et $0$ sinon. Notons cependant que $H_2(\Sigma,\mathbb{Z}/2\mathbb{Z})$ est isomorphe à $\mathbb{Z}/2\mathbb{Z}$ même pour une surface fermée non-orientable. C’est une illustration non triviale du théorème des coefficients universels. Nous expliquons cela en détails dans l’article :
Concentrons-nous sur le premier groupe d’homologie. Une fois qu’on connaît le groupe fondamental d’une surface $\Sigma$, on peut en déduire $H_1(\Sigma,\mathbb{Z})$ en utilisant le théorème de Hurewicz, qui affirme entre autres que ce premier groupe d’homologie est isomorphe à l’abélianisé du groupe fondamental. On prouve ainsi que le premier groupe d’homologie de la surface de genre $g$ est isomorphe à $\mathbb{Z}^{2g}$.
Il peut être intéressant de retrouver ce résultat par d’autres méthodes. Une première méthode consiste à calculer explicitement l’homologie polyédrale de la surface en partant d’une décomposition polyédrale très simple de $\Sigma$. Cette approche est développée dans le cours vidéo :
Une autre méthode consiste à appliquer récursivement la suite exacte de Mayer—Vietoris, qui permet de calculer l’homologie d’un recollement. On commence par calculer l’homologie d’un cercle et d’une sphère, puis on en déduit l’homologie du tore et des surfaces de genre supérieur.
Recollements en dimension $3$ et groupe modulaire

- Un corps en anses de genre $1$, aussi appelé tore solide. Miam !
De même que l’on peut obtenir toutes les surfaces fermées en recollant des morceaux simples le long de leur bord, on peut obtenir toutes les variétés fermées de dimension $3$ en recollant des variétés de dimension $3$ à bord relativement simples (par exemple, des corps en anses) le long de leurs bords, qui sont alors des surfaces fermées.
On pourrait croire que cette approche permet de décrire facilement toutes les variétés de dimension $3$. Mais on se heurte rapidement à un obstacle de taille. En effet, il existe de très nombreuses façons d’identifier deux surfaces homéomorphes, et autant de façons de recoller des morceaux de variétés de dimension $3$ !
Les différentes façons d’identifier deux surfaces fermées homéomorphes sont codées dans un groupe appelé groupe modulaire de la surface. Ce groupe est défini de la façon suivante :
Le groupe modulaire d’une surface $\Sigma$ est le quotient du groupe des homéomorphismes de $\Sigma$ par le sous-groupe des homéomorphismes isotopes à l’identité.
On note $\mathrm{Mod}(\Sigma)$ le groupe modulaire de la surface $\Sigma$ et $\mathrm{Mod}^+(\Sigma)$ le sous-groupe d’indice $2$ formé des homéomorphismes qui préservent l’orientation.
Dans un premier article, nous montrons que, dans le cas de la sphère, ce groupe n’a que deux éléments.
Nous nous intéressons ensuite au tore, puis aux surfaces de genre supérieur. Le groupe modulaire du tore $\mathbb{T}^2$ agit linéairement sur $H_1(\mathbb{T}^2) \simeq \mathbb{Z}^2$ et nous montrons qu’il est en fait isomorphe à $\mathrm{GL}(2,\mathbb{Z})$. Pour les surfaces de genre supérieur, les choses sont plus compliquées. Nous expliquons simplement que le groupe modulaire se surjecte sur le groupe des automorphismes du premier groupe d’homologie qui préservent (au signe près) la forme d’intersection.
Ces articles ne donnent qu’un bref aperçu du groupe modulaire, qui a été abondamment étudié et fait encore l’objet de recherches actives de nos jours. Par exemple, on ne sait toujours pas si le groupe modulaire d’une surface de genre supérieur à $2$ est linéaire, c’est-à-dire s’il admet un morphisme injectif vers un groupe de matrices. La topologie des surfaces, qui a maintenant plus de 150 ans, a encore de longues années devant elle !
[1] Nous décrivons une partie du contenu de son article dans notre page La théorie de Morse, de la topographie à la conjecture de Poincaré en grande dimension.

