Revêtement universel de quelques surfaces

Au fil de l’Introduction à l’Analysis Situs par les surfaces, nous avons vu qu’il est souvent possible de décrire une surface $\Sigma$ comme un polyèdre $P$ dont on a recollé certains bords. En recollant intelligemment plusieurs copies de $P$ (le plus souvent, une infinité), on obtient une surface $E$ qui a la propriété d’être simplement connexe, c’est-à-dire que tout chemin fermé dessiné sur $E$ peut être déformé continûment en un chemin "trivial", qui reste en un point. Cet espace $E$ est muni d’un pavage abstrait par des copies de $P$, et la surface $\Sigma$ s’identifie au quotient de $E$ par un groupe de symétries $\Gamma$ du pavage qui agit simplement transitivement sur les pavés. On conclut que $E$ est le revêtement universel de $\Sigma$, et $\Gamma$ sont groupe fondamental. La preuve de ce théorème de Poincaré est présentée dans le cours moderne.

Quelques exemples

Les vidéos suivantes illustrent ce théorème sur quelques exemples, pour lesquels il est possible de réaliser ce pavage abstrait de façon "géométrique".

Commençons par le cylindre :

Vient ensuite la bande de Möbius :

Remarquons que le cylindre et la bande de Möbius ont le même revêtement universel et que leurs groupes fondamentaux sont isomorphes. Il ne suffit donc pas en général de connaître le groupe fondamental et le revêtement universel d’une surface pour la caractériser. (En revanche, cela suffit si on se restreint aux surfaces fermées.)

On continue avec le tore :

Puis la bouteille de Klein :

Groupe fondamental de la surface de genre $g$

Nous allons maintenant décrire le groupe fondamental de la surface de genre $g$. Dans l’article "Classification des surfaces triangulées par réduction à une forme normale", il est expliqué pourquoi la surface de genre $g$ peut être décrite comme recollement d’un polygone à $4g$ côtés. On pourra s’en convaincre en regardant l’animation suivante, qui traite de la surface de genre $3$.

Une animation analogue pour de la surface de genre 2

Essayons de décrire le groupe fondamental de la surface $\Sigma_2$ de genre $2$ vue comme espace d’identification du polyèdre suivant :

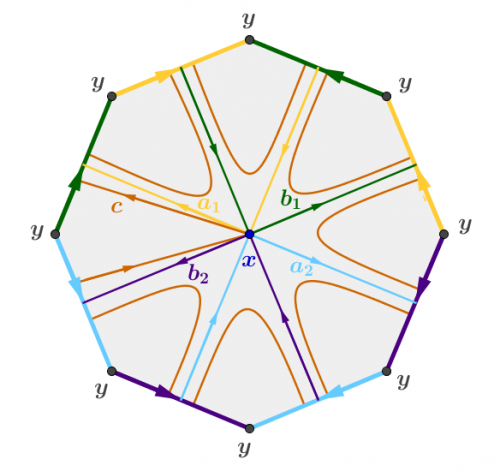
Si on recolle deux par deux les arêtes de même couleur de cet octogone (en suivant l’orientation indiquée par les flèches), on obtient une surface de genre $2$, dans laquelle tous les sommets de l’octogone sont identifiés à un unique point $y$.

Rappelons que le groupe fondamental peut être vu comme le groupe des lacets sur $\Sigma$ partant d’un point base $x$, modulo homotopie. Sur la figure qui précède, nous avons placé le point $x$ au centre du polygone et nous avons représenté quatre lacets, nommés $a_1$, $b_1$, $a_2$ et $b_2$ (respectivement en jaune, vert, bleu et violet). [1] Chacun de ces lacets part de $x$, sort du polygone par une arête, re-rentre par l’arête conjuguée et revient vers $x$.

Considérons maintenant un lacet quelconque dans $\Sigma$ basé en $x$. On peut décomposer se lacets en arcs qui rentrent du polygone par une arête et ressortent par une autre arête. chaque arc peut être transformé continûment en un arc ayant les mêmes extrémités et qui passe par le point base $x$. On obtient ainsi un nouveau lacet homotope au lacet initial. Entre deux passages par $x$, ce nouveau lacet ne fait que sortir par une arête, re-rentrer par l’arête conjuguée et revenir à $x$. Il suit donc un des lacets $a_1$, $b_1$, $a_2$, $b_2$ ou leurs inverses. On en déduit que $a_1$, $b_1$, $a_2$ et $b_2$ engendrent $\pi_1(\Sigma)$.

Considérons maintenant le lacet $c$ représenté sur la figure précédente. En l’observant bien, on constate que ce lacet va de $x$ vers $y$, fait une fois le tour de $y$ dans le sens direct et revient vers $x$. Ce lacet est donc homotopiquement trivial. Or, ce lacet suit successivement les lacets $a_1$, $b_1$, $a_1^{-1}$, $b_1^{-1}$, $a_2$, $b_2$, $a_2^{-1}$ et $b_2^{-1}$. On peut donc conclure que le produit

$$a_1 b_1 a_1^{-1} b_1^{-1} a_2 b_2 a_2^{-1} b_2^{-1}$$

est trivial dans $\pi_1(\Sigma_2)$.

Le théorème du domaine fondamental de Poincaré affirme que c’est la seule relation entre les $a_i$ et $b_i$. On a donc obtenu une présentation du groupe fondamental de $\Sigma_2$ par générateurs et relations, qui se note :

$$\pi_1(\Sigma_2) = \left \langle a_1, b_1, a_2, b_2 \mid a_1 b_1 a_1^{-1} b_1^{-1} a_2 b_2 a_2^{-1} b_2^{-1}= \mathbf{1}\right \rangle~.$$

On peut montrer de façon similaire que le groupe fondamental de la surface $\Sigma_g$ de genre $g$ admet la présentation suivante :

$$\pi_1(\Sigma_g) = \left \langle a_1, b_1, \ldots, a_g, b_g \mid a_1 b_1 a_1^{-1} b_1^{-1} \ldots a_g b_g a_g^{-1} b_g^{-1}= \mathbf{1}\right \rangle~.$$

Il n’est pas simple de se représenter le revêtement universel de la surface de genre $2$. En effet, il est impossible de paver le plan euclidien par des octogones. En revanche, on peut visualiser ce "pavage abstrait" comme un pavage du plan hyperbolique. On en déduit que le revêtement universel de la surface de genre $2$ (et plus généralement celui des surfaces de genre $g \geq 2$) est homéomorphe à un disque.