Groupe fondamental d’une variété polyédrique

Espaces polyédriques

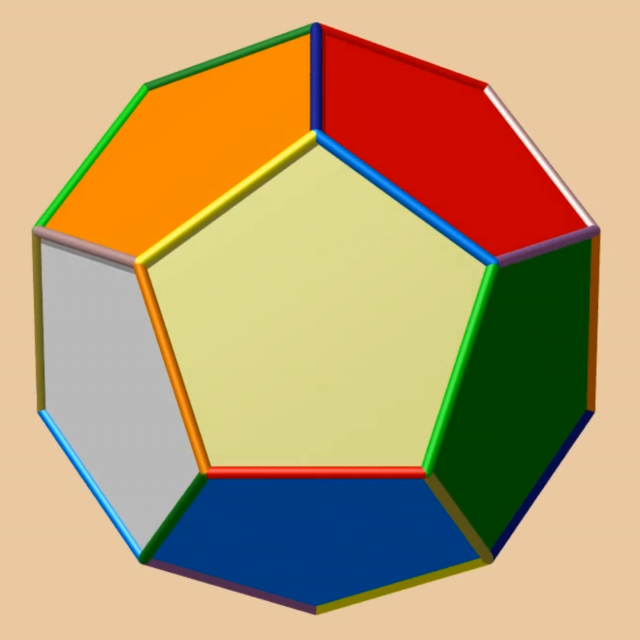
Considérons un polyèdre $P \subset \mathbb{R}^d$ avec un nombre pair de faces identifiées par paires $(F_i^-,F_i^+)$, $i=1, \ldots , m$, comme ici. Notons $\sim$ la relation d’équivalence engendrée par ces identifications de faces.

Le quotient $[P]:=P/\sim$ hérite d’une décomposition cellulaire avec $c_0$ sommets, $c_1$ arêtes, $\ldots$ Le $1$-squelette de cette décomposition cellulaire se rétracte sur un bouquet de $c_1-c_0+1$ cercles. En appliquant le corollaire du théorème de Van Kampen selon lequel le groupe fondamental d’un complexe cellulaire est isomorphe au groupe fondamental de son $2$-squelette, on obtient alors une présentation du groupe fondamental de $[P]$ avec $c_1-c_0+1$ générateurs (un par cercle) et $c_2$ relations (une par $2$-cellule).

Dans l’Analysis Situs, en supposant que le quotient $[P]$ est une variété $V$, Poincaré propose une autre méthode de « calcul » du groupe fondamental de $[P]$, duale de la précédente. Cette méthode conduit à une présentation du groupe fondamental avec un générateur par paire de faces de $P$ (c’est-à-dire par $2$-cellule de $V$) et une relation par cycle d’arêtes (c’est-à-dire par $1$-cellule de $V$). Ces quantités correspondent aux nombres de $1$ et $2$-cellules du $2$-complexe dual à celui considéré jusqu’ici.

Il est fréquent de parvenir à réaliser une variété $V$ comme quotient $G \backslash E$ d’un espace simplement connexe $E$ par un groupe discret opérant librement et proprement sur $E$. Vu comme groupe d’automorphismes du revêtement universel $E \to V$ le groupe $G$ est alors isomorphe au groupe fondamental de $V$. C’est cette méthode — que nous décrivons ici — qu’utilise Poincaré pour calculer les groupes fondamentaux des variétés polyédriques.

Relations de Poincaré

On représente par le symbole $a_i$ la transformation qui identifie la face $F_i^-$ à la face $F_i^+$. On peut aussi penser à $a_i$ comme à (la classe d’homotopie d’)un lacet dans le quotient $[P]$, pointé au centre de $P$, qui consiste à sortir par la face $F_i^+$ pour revenir par la face opposée $F_i^-$ et rejoindre le point base. On représente alors par le symbole $a_i^{-1}$ la transformation réciproque (ou encore le chemin $a_i$ parcouru dans le sens opposé). Il n’est pas difficile de se convaincre que les lacets $a_i$ $(i=1, \ldots , m)$ engendrent le groupe fondamental du quotient $[P]$.

Poincaré associe à chaque classe de faces de codimension $2$ dans le quotient $[P]$ une relation entre les $a_i$ dite relation de Poincaré : une face de codimension $2$ de $P$ est l’intersection de deux faces $F_i^{\epsilon} \cap F_j^{\epsilon'}$, où $\varepsilon$ et $\varepsilon'$ sont des signes ; on peut donc représenter une classe de face de codimension $2$ par une suite d’indices $(i_1 , \ldots , i_t )$ et une suite de signes $(\varepsilon_1 , \ldots , \varepsilon_t )$ de sorte que les faces de codimension $2$ qui constituent cette classe soient : [1]

$$F_{i_t}^{-\varepsilon_t} \cap F_{i_1}^{\varepsilon_1} , F_{i_1}^{-\varepsilon_1} \cap F_{i_2}^{\varepsilon_2} , F_{i_2}^{-\varepsilon_2} \cap F_{i_3}^{\varepsilon_3} , \ldots , F_{i_{t-1}}^{-\varepsilon_{t-1}} \cap F_{i_t}^{\varepsilon_t}.$$

La relation de Poincaré correspondante est

$$a_{i_1}^{\varepsilon_1} a_{i_2}^{\varepsilon_2} \cdots a_{i_t}^{\varepsilon_t}.$$

(Ici on identifie un signe $\pm$ à $\pm1$.)

Vu comme lacet dans le quotient $[P]$ l’expression ci-dessus consiste à tourner autour de la face de codimension $2$ associée. Un tel lacet est en particulier homotope au lacet constant. Autrement dit, le groupe abstrait $G$ défini par la présentation

$$G = \langle a_1 , \ldots , a_m \; \big| \;\mbox{ relations de Poincaré } \rangle$$

se surjecte sur le groupe fondamental de l’espace quotient $[P]$.

Le théorème de Poincaré

Si l’on suppose de plus que l’espace quotient $[P]$ est une variété $V$, Poincaré montre que $G$ est en fait isomorphe au groupe fondamental de $V$.

Démonstration. Dans un premier temps on associe au polyèdre $P$ et au groupe $G$ un espace simplement connexe $E$, appelé pavage abstrait. Puis nous montrerons que l’espace $E$ revêt naturellement la variété $V$ et que $G$ s’identifie au groupe des automorphismes de ce revêtement.

On commence par définir le pavage abstrait comme espace quotient

$$E = (P \times G)/ \simeq$$

où $G$ est muni de la topologie discrète et $\simeq$ est la relation d’équivalence engendrée par :

$$(p , g) \simeq (a_i p , g a_i^{-1}) \quad p \in F_i^- , \ g \in G , \ i = 1, \ldots , m.$$

Noter qu’alors $a_i p$ appartient à la face $F_i^+$.

Notons $[p,g]$ la classe de $(p,g)$ dans $E$. Le groupe $G$ opère naturellement à gauche sur $E$. Étant donné un sous-ensemble $A$ de $P$, on pose

$$[A] = \{ [p,1] \; | \; p \in A \}.$$

Alors pour $g \in G$ on a :

$$g[A] = \{ [p,g] \; | \; p \in A \}.$$

Les sous-ensembles $g[\mathrm{int}( P)]$ ($g \in G$) sont deux à deux disjoints dans $E$ ; on appelle pavés leurs adhérences $g[P]$. L’image $[F_i^{\pm}]=a_i^{\pm1} [F_i^{\mp}]$ d’une face de $P$ est commune à exactement deux pavés : $[P]$ et $a_i^{\pm 1} [P]$. Puisque $G$ est engendré par les $a_i$, on en conclut que l’espace $E$ est connexe.

Considérons maintenant l’application $\pi : E \to V$ qui à un élément $[p,g]$ de $E$ associe la classe de $p$ dans $V$. L’application $\pi$ est clairement continue et $G$-invariante. On veut montrer que $\pi$ est un revêtement.

Soit $P_0$ le polyèdre $P$ privé de ses faces de codimension $>2$. Posons

$$E_0 = \bigcup_{g \in G} g [P_0] .$$

Montrons d’abord que la restriction de $\pi$ à $E_0$ induit un revêtement de $E_0$ sur l’image $V_0$ de $P_0$ dans $V$ :

$$\pi_0 : E_0 \to V_0.$$

Soit $x \in V_0$, il s’agit de trouver un voisinage ouvert de $x$ au-dessus duquel $\pi_0$ est un revêtement trivial.

Si $x$ appartient à l’image de $\mathrm{int} (P )$ dans $V_0$ alors on peut prendre $U$ égal à l’image de $\mathrm{int} ( P)$ dans $V$ et

$$\pi^{-1} (U) = \bigsqcup_{g \in G} g[\mathrm{int} ( P)].$$

Puis, si $x$ appartient à l’image dans $V_0$ de l’intérieur d’une face $F_i^{\pm}$ de $P$, on peut prendre $U$ égal à n’importe quel petit voisinage ouvert de $x$ dans $V$ dont la préimage dans $P$ est égale à la réunion disjointe d’un ouvert $O_-$ contenu dans $\mathrm{int} ( P) \cup \mathrm{int} (F_i^{-})$ et d’un ouvert $O_+$ contenu dans $\mathrm{int} ( P) \cup \mathrm{int} (F_i^{+})$. On a alors :

$$\pi^{-1} (U) = \bigsqcup_{g \in G} g([O_-] \cup a_i^{- 1} [O_+]).$$

Enfin si $x$ appartient à l’image dans $V_0$ de l’intérieur d’une face de codimension $2$ dans $P$, alors il correspond à $x$ une suite d’indices $(i_1 , \ldots , i_t)$ et une suite de signes $(\varepsilon_1 , \ldots , \varepsilon_t )$ telles que

1. le pont $x$ appartient à l’image de la face de codimension $2$ égale à l’intersection $F_{i_t}^{\mp} \cap F_{i_1}^{\pm}$, et
2. la classe de $\sim$-équivalence de $F_{i_t}^{-\varepsilon_t} \cap F_{i_1}^{\varepsilon_1}$ est constituée des faces de codimension $2$ suivantes :

   $$F_{i_t}^{-\varepsilon_t} \cap F_{i_1}^{\varepsilon_1} , F_{i_1}^{-\varepsilon_1} \cap F_{i_2}^{\varepsilon_2} , F_{i_2}^{-\varepsilon_2} \cap F_{i_3}^{\varepsilon_3} , \ldots , F_{i_{t-1}}^{-\varepsilon_{t-1}} \cap F_{i_t}^{\varepsilon_t}.$$

Il s’en suit que la classe de $\simeq$-équivalence de $(x,1)$ dans $P\times G$ est précisément

$$\{ (x,1) , (a_{i_1}^{-\varepsilon_1} x , a_{i_1}^{\varepsilon_1}) , (a_{i_2}^{-\varepsilon_2} a_{i_1}^{-\varepsilon_1} x , a_{i_1}^{\varepsilon_1} a_{i_2}^{\varepsilon_2}), \ldots , (a_{i_{t-1}}^{-\varepsilon_{t-1}} \cdots a_{i_1}^{\varepsilon_1} x , a_{i_1}^{\varepsilon_1} \cdots a_{i_{t-1}}^{\varepsilon_{t-1}}) \}.$$

Posons $g_1 = 1$ et $g_j = a_{i_1}^{\varepsilon_1} \cdots a_{i_{j-1}}^{\varepsilon_{j-1}}$ pour $j=2 , \ldots , t$. On peut prendre $U$ égal à n’importe quel petit voisinage ouvert de $x$ dans $V$ dont la préimage dans $P$ est égale à la réunion disjointe de $t$ ouverts

$$O_j \subset \mathrm{int} ( P) \cup \mathrm{int} (F_{i_{j-1}}^{-\varepsilon_{j-1}}) \cup \mathrm{int} (F_{i_{j}}^{\varepsilon_j}) \cup \mathrm{int} (F_{i_{j-1}}^{-\varepsilon_{j-1}} \cap F_{i_{j}}^{\varepsilon_j}).$$

On a alors :

$$\pi^{-1} (U) = \bigsqcup_{g \in G} g( \cup_{j=1}^t g_j [O_j] ).$$

L’application $\pi_0 : E_0 \to V_0$ est donc un revêtement. Mais puisque $V$ est une variété, le link de chaque cellule du complémentaire de $V_0$ dans $V$ est simplement connexe. L’application $\pi_0$ restreinte à ce link induit donc un revêtement trivial sur son image et son extension linéaire à l’étoile est encore un revêtement (trivial). On en déduit que $\pi$ est bien un revêtement.

Noter que $G$ est précisément le groupe des automorphismes du revêtement $p:E \to V$. Pour conclure il reste donc à montrer que l’espace $E$ est simplement connexe. Pour cela il suffit de montrer que $E_0$ est simplement connexe. Mais cela découle de la construction (et des relations de Poincaré) : un lacet qui entoure une face de codimension $2$ dans $E_0$ est homotopiquement trivial.

$$ $$

On applique le théorème du domaine fondamental aux exemples 1, 2, 3 et 4 des recollements du cube considérés par Poincaré au § 10 de l’Analysis Situs. On l’applique encore à l’étude de la variété dodécaédrique de Poincaré et à l’étude de la variété dodécaédrique de Seifert-Weber.

Une autre démonstration du théorème de Poincaré

On peut aussi déduire le théorème de Poincaré du théorème de Van Kampen.

Notons $P_k$ le polyèdre privé d’un voisinage régulier de son $k$-squelette. Puisque les identifications envoient sommet sur sommet, arête sur arête, $\ldots$, on peut procéder sur $P_k$ aux mêmes identifications que sur $P$, pourvu que les voisinages réguliers que l’on a enlevés soient compatibles avec les identifications, ce qui se peut faire. On obtient ainsi des ouverts emboîtés

$$V_1 = \left[ P_{d-1} \right] \subset V_2 = \left[ P_{d-2} \right] \subset V \subset \cdots.$$

Ici on note $[A]$ l’image dans $V$ d’un sous-ensemble $A$ de $P$. Mais puisque $V$ est une variété, le bord d’un voisinage régulier de chaque cellule de son $(d-3)$-squelette est simplement connexe. Le groupe fondamentale de $V$ est donc isomorphe au groupe fondamental de $V_2$.

Maintenant, le polyèdre « raboté » $P_1$ se rétracte par déformation sur un graphe $\Gamma$ ayant pour sommets le centre $q$ de $P$ et les centres $q_i^-$ et $q_i^+=a_i (q_i^-)$ des faces $F_i^-$ et $F_i^+$ ($i=1 , \ldots , m$) et pour arêtes des segments joignant les $q_i^\pm$ à $q$. On peut même trouver une rétraction qui soit compatible avec les différentes identifications, de telle sorte que l’ouvert $V_1 = \left[P_1\right]$ se rétracte sur l’image $\left[\Gamma\right]$, qui est un bouquet de $m$ cercles. Le groupe fondamental de $V_1$ est donc un groupe libre engendré par $m$ symboles $a_1, \ldots , a_m$ correspondants aux $m$ boucles.

On obtient enfin $V_2$ à partir de $V_1$ en ajoutant un voisinage régulier de l’image des arêtes ouvertes dans $V$. Autrement dit, $V_2$ est homéomorphe à l’union de $V_1$ et de $c_1$ boules $B_{j}$, $j=1 , \ldots , c_1$. D’après le théorème de van Kampen, le groupe fondamental de $V_2$ est le quotient de celui de $V_1$ par le sous-groupe distingué engendré par les éléments de

$$\bigcup_{j=1}^{c_1} \mathrm{im}(\pi_1(B_{j} \cap V_1) \to \pi_1(V_1)).$$

Or, chaque ouvert $B_{j} \cap V_1$ se rétracte par déformation sur une courbe $\gamma_{j}$ qui fait un petit tour autour d’une face de codimension $2$ de $V$ et qui est homotope à

$$a_{i_1}^{\varepsilon_1} a_{i_2}^{\varepsilon_2} \cdots a_{i_t}^{\varepsilon_t}.$$

si

$$F_{i_t}^{-\varepsilon_t} \cap F_{i_1}^{\varepsilon_1} , F_{i_1}^{-\varepsilon_1} \cap F_{i_2}^{\varepsilon_2} , F_{i_2}^{-\varepsilon_2} \cap F_{i_3}^{\varepsilon_3} , \ldots , F_{i_{t-1}}^{-\varepsilon_{t-1}} \cap F_{i_t}^{\varepsilon_t}.$$

est la classe d’équivalence de la face de codimension $2$ de $P$ correspondante.