Variété dodécaédrique de Seifert-Weber

On s’intéresse ici à un espace d’identification du dodécaèdre. La construction est similaire à celle de la variété dodécaédrique de Poincaré. Une partie des détails sera donc omise et laissée en exercice. L’espace obtenu, en revanche, est très différent de celui de Poincaré : c’est aussi une variété, mais celle-ci peut être munie d’une géométrie hyperbolique, alors que celle de Poincaré possédait une structure sphérique. Ce nouvel espace dodécaédrique est en particulier intéressant car il fournit un exemple de variété hyperbolique qui n’est pas Haken d’après Burton, Rubinstein and Tillmann [1].

Définition et premières propriétés.

On a considéré là le quotient du dodécaèdre ${\mathcal P}$ obtenu en identifiant les faces opposées après un dixième de tour. Ici, on s’intéresse au recollement $W$ dans lequel les faces opposées sont identifiées après trois dixièmes de tour. Une différence minime, semble-t-il, mais nous allons voir que les deux variétés obtenues ont des propriétés tout-à-fait différentes.

Notons, comme nous l’avons fait dans l’article susmentionné, que les autres recollements possibles pour lesquels toutes les paires de faces opposées sont identifiées de la même façon donnent soit l’espace projectif réel $\mathbb{RP}^3$ (cas où l’on recolle après un demi tour) soit à nouveau l’un des deux espaces dodécaédraux étudiés (Poincaré ou Seifert-Weber) avec l’orientation opposée, à cause des symétries du dodécaèdre. Bien sûr, on peut ne pas identifier toutes les paires de faces opposées de la même façon, ou même ne pas identifier nécessairement des paires de faces opposées. Toutefois, les espaces d’identification obtenus ainsi n’héritent plus alors des symétries du dodécaèdre.

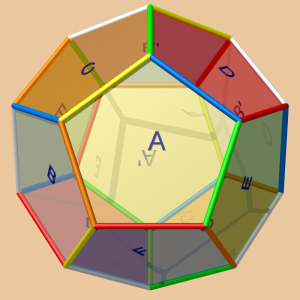
Comme dans le cas de l’espace dodécaédrique de Poincaré, on note $A,A'$, $B,B'$, $C,C'$, $D,D'$, $E,E'$ et $F,F'$ les paires de faces opposées du dodécaèdre. Mais on note cette fois-ci $y$, $x_1$, $x_2$, $x_3$, $x_4$ et $x_5$ les transformations de $A$ vers $A'$, $B$ vers $B'$ etc... définissant $W$ comme espace d’identification, pour insister sur la symétrie d’ordre $5$ permutant cycliquement les faces adjacentes à $A$ [2]. Dans la vidéo ci-dessous, on voit que ces transformations identifient les arêtes par cinq. A chaque classe d’arête correspond une couleur sur la figure suivante. On peut également vérifier que tous les sommets sont identifiés entre eux.

La décomposition polyédrale de $W$ induite par celle de ${\mathcal P}$ comporte donc une unique $3$-cellule, six faces, six arêtes et un unique sommet. La caractéristique d’Euler-Poincaré de $W$ est donc zéro, et on déduit d’un critère général que $W$ est une $3$-variété topologique.

Comme pour l’espace dodécaédrique de Poincaré, une présentation du groupe fondamental de $W$ peut être obtenue en applicant le théorème du domaine fondamental de Poincaré dans sa version topologique. A chaque classe d’arête correspond une relation, ce qui en fait six au total. On peut prendre comme ensemble de représentants des classes d’arêtes les cinq arêtes de la face $A$ et l’arête $B\cap E'$ par exemple. Les cinq premières relations s’obtiennent alors l’une à partir de l’autre par permutation circulaire des indices. Décrivons explicitement l’une de ces classes d’arêtes :

$$B\cap A\overset{y}{\mapsto}A'\cap F'\overset{x_{5}^{-1}} {\mapsto}F\cap E \overset{x_{4}}{\mapsto}E'\cap C \overset{x_{2}}{\mapsto}C'\cap B'\overset{x_1^{-1}}{\mapsto}B\cap A.$$

Il lui correspond le mot $y^{-1}x_5x_4^{-1}x_2^{-1}x_1$. Plus généralement, aux cinq classes du premier type correspondent les mots $y^{-1}x_{i-1}x_{i-2}^{-1}x_{i+1}^{-1}x_i$, $i=1,\dots,5$, les indices étant pensés modulo $5$. La dernière classe d’arête est :

$$E'\cap B\overset{x_1}{\mapsto}B'\cap D\overset{x_3}{\mapsto}D'\cap F \overset{x_5}{\mapsto}F'\cap C\overset{x_2}{\mapsto}C'\cap E\overset{x_4} {\mapsto}E'\cap B,$$

ce qui donne finalement la présentation :

$$\pi_1(W)=\langle y,x_1,x_2,x_3,x_4,x_5 \; | \; \{ y^{-1}x_{i-1}x_{i-2}^{-1}x_{i+1}^{-1}x_i\}_{1\le i\le 5 },\, x_4x_2x_5x_3x_1\rangle.$$

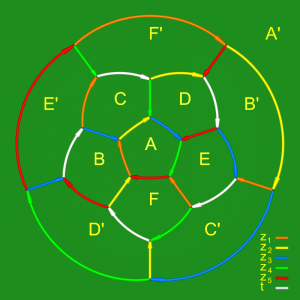
Puisque la décomposition polyédrale de $W$ ne comporte qu’un sommet, une présentation du groupe fondamental peut aussi être obtenue en utilisant le $2$-squelette. Soient $z_i$, $i=1,\dots,5$, les lacets images des arêtes de $A$ et $t$ le lacet image de la dernière classe d’arêtes, les orientations étant précisée sur la figure ci-dessous, qui représente une projection stéréographique du bord du dodécaèdre.

On a alors la présentation

$$\pi_1(W)=\langle z_1,z_2,z_3,z_4,z_5,t \; | \; \{ z_{i+1}^{-1}z_{i-1}tz_{i+2}z_i^{-1}\}_{1\le i\le 5},\ z_1z_2z_3z_4z_5\rangle$$

où la dernière relation se lit autour de la face $A,A'$ et les autres autour des autres paires de faces. On sait abstraitement que les groupes ayant ces deux présentations sont isomorphes. On peut d’ailleurs vérifier que les correspondances :

$$y \mapsto t,\; x_1 \mapsto z_1^{-1},\; x_2 \mapsto z_4^{-1},\; x_3 \mapsto z_2^{-1},\; x_4 \mapsto z_5^{-1},\; x_5 \mapsto z_3^{-1}$$

définissent un tel isomorphisme.

Pour calculer le premier groupe d’homologie de $W$ il suffit d’abélianiser l’une des deux présentations, par exemple la première. On utilisera les mêmes symboles pour les générateurs du $\pi_1$ et du $H_1$ mais avec notation additive pour ces derniers.

On explicite $x_5$ en fonction des autres grâce à la dernière relation :

$$x_5=-(x_1+x_2+x_3+x_4)$$

et $y$ grâce à la première relation, pour $i=3$ :

$$y=(x_2+x_3)-(x_1+x_4).$$

En remplaçant dans les autres relations on a alors

$$\begin{cases} x_1-3x_2-2x_3-x_4=0 \\ 3x_1+x_2-x_3+2x_4=0 \\ 2x_1-x_2+x_3+3x_4=0 \\ -x_1-2x_2-3x_3+x_4=0 \\ \end{cases}$$

et on peut expliciter $x_4=x_1+2x_2+3x_3$ en utilisant la dernière relation. On a alors

$$\begin{cases} -5(x_2+x_3)=0 \\ 5(x_1+x_2+x_3)=0 \\ 5(x_1+x_2+2x_3)=0 \\ \end{cases}$$

Les éléménts $\alpha=x_2+x_3$, $\beta=x_1+x_2+x_3$ et $\gamma=x_1+x_2+2x_3$ forment un système de générateurs du $H_1$. En effet $x_1=\beta -\alpha$, $x_3=\gamma-\beta$ et $x_2=\alpha+\beta-\gamma$. Les trois relations restantes ci-dessus montrent donc que $H_1(W)\cong (\mathbb{Z}/5)^3$.

La structure hyperbolique de $W$.

Comme pour l’espace dodécaédrique de Poincaré, il est possible de munir $W$ d’une structure géométrique toujours grâce au théorème de Poincaré sur les domaines fondamentaux, dans sa version géométrique. Pour $W$, cependant, la structure sera hyperbolique et non sphérique. Encore une fois, il suffit de construire un dodécaèdre hyperbolique totalement symétrique et avec les bons angles dièdres : les angles dièdres doivent mesurer dans ce cas $2\pi/5$ car les arêtes sont identifiées cinq à cinq.

Démonstration. Le même raisonnement vu pour l’espace dodécaédrique de Poincaré permet de ramener la construction du dodécaèdre hyperbolique régulier à la construction d’un tétraèdre avec trois angles dièdres droits, deux angles dièdres qui mesurent $\pi/5$ et un qui mesure $\pi/3$.

La stratégie est identique à celle vue dans le cas sphérique : il suffit de construire les plans hyperboliques qui délimitent le tétraèdre en imposant qu’ils s’intersectent avec les bons angles. Puisque l’angle dièdre entre deux plans dans l’espace hyperbolique coïncide avec l’angle entre les traces des deux plans sur la sphère à l’infini de $\mathbb{H}^3$, le problème est réduit à trouver un système de quatre cercles de Möbius (à savoir, des cercles ou des droites) dans le plan ayant les bons angles d’intersection.

Soient $H_i$, $i=1,\dots,4$, les quatre plans hyperboliques comme montré dans le dessin ci dessus : les angles dièdres qui mesurent $\pi/5$ sont ceux entre $H_2$ et $H_3$ et entre $H_1$ et $H_4$, et l’angle dièdre qui mesure $\pi/3$ est celui entre $H_2$ et $H_4$. Tous les autres angles sont droits.

On commence par fixer la trace de $H_i$ : elle sera le cercle unité du plan. On fixe ensuite les traces de $H_2$ et $H_3$ qui doivent rencontrer la trace de $H_1$ perpendiculairement. La trace de $H_3$ sera la droite $y=0$ et la trace de $H_2$ la droite $y=\tan(\pi/5) x$ qui passent toutes les deux par le centre du cercle unité. Puisque $H_4$ rencontre $H_3$ en un angle droit, sa trace sera un cercle centré sur la droite $y=0$ dont il faut detrminer le centre $C=(a,0)$ et le rayon $r$. Par symétrie de la construction et sans perte de généralité on peut supposer que $a>0$. Puisque $H_4$ rencontre $H_2$ en un angle de $\pi/3$, le pont $P$ intersection du cercle recherché avec la droite $y=\tan(\pi/5) x$ sera tel que l’angle $\angle OPC$ mesure $\pi/6$. Par ailleurs, l’intersection $T=(x_T,y_T)$ de ce cercle avec le cercle unitaire doit être tel que l’angle $\angle OTC$ mesure $\pi/5$. On notera qu’il y a deux points d’intersection entre ces cercles, symétriques par rapport à l’axe des $x$. Soit $T$ le point d’intersection tel que $y_T>0$.

$$ $$

Fixons maintenant $C=(a,0)$. Le rayon $r$ du cercle par $C$ est déterminé par la condition sur $\angle OPC$. En effet en applicant le théorème du sinus au triangle $OCP$ on doit avoir $a/r=\sin(\pi/6)/\sin(\pi/5)$. Posons $\lambda=a/r=\sin(\pi/6)/\sin(\pi/5)$. Le théorème du sinus appliqué au triangle $OTC$ dit que la mesure $\alpha$ de l’angle $\angle OTC$ doit satisfaire $\sin(\alpha)/a=y_T/r$ : $C$ sera alors le centre du cercle trace de $H_4$ si et seulement si $\alpha=\pi/5$. Il suffit alors de montrer qu’il existe un $a>0$ qui rempli la condition. Les coordonnées de $T$ doivent satisfaire le système

$$\begin{array}{l} x^2+y^2=1 \\ (x-a)^2+y^2=r^2=(a/\lambda)^2 \end{array}$$

et de façon équivalente

$$\begin{array}{l} x^2+y^2=1 \\ -2ax+a^2+1=(a/\lambda)^2 \end{array}$$

On peut expliciter $x$ comme fonction de $a$ et on vérifie que $2x'=(1-1/\lambda^2)-1/a^2<0$, car $\lambda <1$. La fonction $a\mapsto x(a)$ est donc un homéomorphisme entre $\mathbb{R}^*_+$ et $\mathbb{R}$. On considère $\sin(\alpha)=\lambda\sqrt{1-x^2}$ : sa dérivée $-\lambda x/\sqrt{1-x^2}$ par rapport à $x$ s’annule seulement quand $x=0$ où la fonction a un maximum. Il s’en suit $sin(\alpha_max)= \lambda>\sin(\pi/5)>0$ ce qui assure l’existence d’une solution.

$$ $$

On remarquera que dans la preuve on obtient deux solutions : elles correspondent aux deux possibles positions de $H_4$ par rapport à $H_1$, à savoir au-dessus ou au-dessous.

$$ $$

Une partie des deux paragraphes est repris dans le cours filmé ci-dessous.

$$ $$

L’espace dodécaédrique de Seifert-Weber comme revêtement ramifié de $\mathbb{S}^3$.

Le procédé qui montre que l’espace dodécaédrique de Poincaré est le revêtement à cinq feuillets de $\mathbb{S}^3$ ramifié le long du nœud du trèfle permet de montrer que l’espace dodécaédrique de Seifert-Weber est aussi un revêtement ramifié à cinq feuillets de la $3$-sphère.
Dans ce cas, l’ensemble de ramification n’est pas connexe : il s’agit d’un entrelacs à deux composantes, l’entrelacs de Whitehead. Une des deux composantes est bien évidemment l’image de l’axe de la rotation d’ordre $5$. L’autre composante est l’image d’un cycle d’arêtes de ${\mathcal P}$ qui donne le lacet $b$ dans $W$. En effet ce cycle d’arêtes est laissé invariant par la rotation et le lacet correspondant est donc fixé point par point par l’isométrie d’ordre $5$ de $W$. Cette situation est donc semblable à celle vue lorsqu’on a considéré l’isométrie d’ordre $3$ de l’espace dodécaédrique de Poincaré.
Les dessins qui suivent montrent les simplifications nécessaires pour obtenir le quotient de $W$ par l’action de l’isométrie d’ordre $5$. Les détails, qui suivent de près ce qui a été fait pour l’espace dodécaédrique de Poincaré, sont laissés en exercice.

La vidéo Not Knot illustre en partie cette dernière section.