Dans le cinquième complément à l’Analysis Situs, Poincaré construit une variété qui a la propriété d’avoir les mêmes groupes d’homologie à coefficients entiers que la 3-sphère, mais qui n’est pas homéomorphe à la 3-sphère. Une variété satisfaisant cette propriété est appelée sphère d’homologie entière. Poincaré la définit comme le recollement de deux corps en anses de genre 2, une construction appelée de nos jours scindement de Heegaard.
Poincaré montre que sa « sphère » n’est pas (homéomorphe à) la 3-sphère usuelle en vérifiant que son groupe fondamental se surjecte sur le groupe alterné $A_5$ et ne peut donc pas être trivial.
Cette première sphère d’homologie est d’autant plus remarquable que nous savons maintenant qu’elle est la seule sphère d’homologie entière de dimension 3 dont le groupe fondamental est fini. [1]
La sphère d’homologie de Poincaré peut être décrite de plusieurs façons différentes. Dans l’article « Eight faces of the Poincaré homology 3-sphere », Kirby et Scharlemann en donnent huit descriptions différentes et montrent qu’elles sont toutes équivalentes. Ici, nous allons en proposer six. En général, les preuves des équivalences entre ces six différentes descriptions ne suivront pas les arguments de Kirby et Scharlemann et seront de nature plus combinatoire.
Les six descriptions auxquelles on va s’interesser sont : [2]
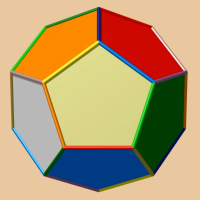
1. La description comme espace d’identification d’un dodécaèdre, c’est-à-dire comme variété obtenue en recollant les faces opposées d’un dodécaèdre.
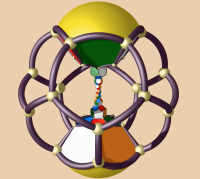
2. La description comme quotient de la 3-sphère par l’action libre d’un sous-groupe de $\mathrm{SU}(2)$ d’ordre 120, parfois appelé groupe des icosions.
3. Une description via un scindement de Heegaard de genre 2 particulièrement simple, obtenu en simplifiant le scindement de Heegaard de genre $6$ provenant de la structure de variété dodécaédrique.
4. La définition originale de Poincaré, via un autre scindement de Heegaard de genre 2. On l’obtient à partir du scindement de Heegaard précédent par une suite d’opérations élémentaires.
5. La description par chirurgie de Dehn sur le nœud du trèfle.
6. La description comme revêtement de $\mathbb{S}^3$ ramifié le long du nœud de trèfle, qui permet en particulier de voir la sphère d’homologie de Poincaré comme une sphère de Brieskorn particulière.
Pour montrer l’équivalence entre ces différentes descriptions, on pourrait faire appel à un « marteau-pilon ». La démonstration de la conjecture de géométrisation par Grigori Perelman implique en effet qu’une variété de dimension 3 dont le groupe fondamental est fini est homéomorphe au quotient de $\mathbb{S}^3$ par l’action d’un groupe fini d’isométries. Un tel groupe est soit cyclique, auquel cas l’espace quotient est une variété lenticulaire, soit une extension centrale d’un groupe diédral, d’un sous-groupe de $S_4$, ou de $A_5$ par un groupe cyclique d’ordre pair. Il en résulte facilement que la variété dodécaédrique de Poincaré est la seule sphère d’homologie à groupe fondamental fini. Nous montrons ici l’équivalence entre les six descriptions ci-dessus de manière « élémentaire ». [3]
Nous partons de la définition comme espace dodécaédrique, et expliquons comment passer de cette description à chacune des cinq autres.
Une application du théorème du domaine fondamental de Poincaré — ou l’étude directe du quotient — permet tout d’abord de réaliser l’espace dodécaédrique comme quotient de la sphère $\mathbb{S}^3$ par l’action d’un groupe d’isometries.
On considère ensuite la décomposition en anses naturelle de l’espace dodécaédrique. En simplifiant cette décomposition par des glissements d’anses et des éliminations d’anses complémentaires nous obtenons d’autres décompositions en anses de l’espace dodécaédrique puis ici le scindement de Heegaard de la définition originale de Poincaré. À chacune des décompositions en anses obtenue correspond une présentation du groupe fondamental de la variété dodécaédrique de Poincaré.
Toujours en faisant des glissements d’anses, on montre ici comment l’espace dodécaédrique de Poincaré peut être obtenu par recollement d’un tore solide sur le complémentaire d’un voisinage tubulaire du nœud du trèfle. On montre ainsi que l’espace dodécadrique peut être obtenu par chirurgie de Dehn. Notre méthode suit de près celle utilisée par Rolfsen dans son livre.
Pour terminer, nous montrons ici pourquoi le quotient de l’espace dodécaédrique de Poincaré par sa symétrie d’ordre $5$ est la $3$-sphère. On en déduit que la projection de l’espace dodécaédrique sur $\mathbb{S}^3$ est un revêtement ramifié sur le nœud de trèfle.
On trouvera enfin d’autres informations sur la sphère d’homologie de Poincaré en parcourant The Manifold Atlas Project.
[1] Comme nous l’expliquons plus bas cela peut se déduire de la conjecture de géométrisation mais c’est plus simplement démontré ici.
[2] On conseille ici de ne pas trop s’écarter de l’ordre de lecture proposé : la seconde et la troisième descriptions reposent en effet sur la première. On aboutit à la définition originale de Poincaré en partant de notre troisième description. De même, la description par chirurgie de Dehn part de la troisième description. Par contre la dernière description, comme revêtement ramifié, part de la première sans utiliser les autres.
[3] Cette démarche présente toutefois l’inconvénient d’être peu conceptuelle. Il s’agit de passer d’un diagramme de Heegaard à un autre donnant la même variété par une suite de manipulations élémentaires. Si cela est toujours possible, il reste que, comme pour passer d’une présentation d’un groupe à une autre, il n’y a pas d’algorithme général.