|
> Exemples de dimension 3 > Topologie des variétés de dimension 3 > Décomposition en anses, diagramme de Heegaard Décomposition en anses, diagramme de Heegaard |
Soient $V_1$ et $V_2$ deux variétés de dimension 3 compactes dont les bords sont homéomorphes et soit $f: \partial V_1 \to \partial V_2$ un homéomorphisme. La variété
$$V= V_1 \cup_f V_2,$$
obtenue en recollant $V_1$ et $V_2$ le long de leur bord à l’aide de l’application $f$, est une variété de dimension 3 compacte sans bord.
Premiers exemples
Recollement de deux boules. La variété obtenue en recollant deux boules de dimension 3 selon leur bord, comme sur l’animation qui suit,
est homéomorphe à la sphère $\mathbb{S}^3$. La projection stéréographique depuis le pôle nord de $\mathbb{S}^3$ identifie en effet l’hémisphère sud de $\mathbb{S}^3$ à la boule unité $\mathbb{B}^3$. Et la projection depuis le pôle sud identifie l’hémisphère nord de $\mathbb{S}^3$ à la boule unité $\mathbb{B}^3$. De cette manière la sphère se trouve décomposée en la réunion de deux boules recollées selon leur bord par l’application identité.
Le lemme suivant, connu sous le nom d’« Alexander trick » permet de montrer que quel que soit l’homéomorphisme de recollement, la variété obtenue en recollant deux boules selon leur bord est encore homéomorphe à la sphère $\mathbb{S}^3$. Un homéomorphisme entre la première boule et l’hémisphère sud dans $\mathbb{S}^3$ s’étend en effet en un homéomorphisme de toute la variété vers $\mathbb{S}^3$.
Tout homéomorphisme $f : \mathbb{S}^2 \to \mathbb{S}^2$ s’étend en un homéomorphisme $F: \mathbb{B}^3 \to \mathbb{B}^3$.
Démonstration. On définit $F: \mathbb{B}^3 \to \mathbb{B}^3$ par la formule :
$$F( t \cdot \mathbf{x} ) = t \cdot f(\mathbf{x} ) , \quad t \in [0,1], \ \mathbf{x} \in \mathbb{S}^2.$$
C.Q.F.D.
$$ $$
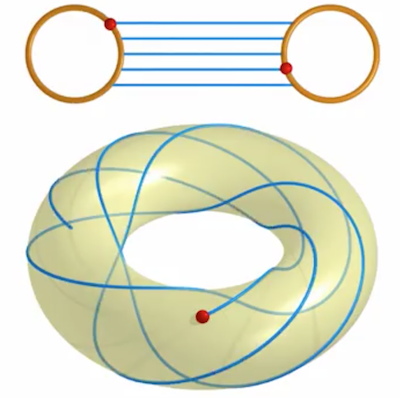
Recollement de deux tores solides Le recollement de deux tores solides $\mathbb{S}^1 \times \mathbb{D}^2$ en prenant $f$ égale à l’identité donne la variété $\mathbb{S}^1 \times \mathbb{S}^2$. Toutefois si l’on prend pour $f$ l’homéomorphisme
$$\mathbb{S}^1 \times \mathbb{S}^1 \to \mathbb{S}^1 \times \mathbb{S}^1 ; \ (x,y) \mapsto (y,x )$$
la variété obtenue est la sphère $\mathbb{S}^3$. Cette décomposition de la sphère comme réunion de deux tores solides est un cas particulier de la fibration de Hopf comme le montre l’animation suivante.
On peut aussi remarquer que, la boule de dimension 4 étant homéomorphe au produit $\mathbb{D}^2 \times \mathbb{D}^2$, on a :
$$\mathbb{S}^3 = \partial (\mathbb{D}^2 \times \mathbb{D}^2 ) = (\mathbb{S}^1 \times \mathbb{D}^2) \cup (\mathbb{D}^2 \times \mathbb{S}^1 )$$
qui est une décomposition de la sphère $\mathbb{S}^3$ comme réunion de deux tores solides selon leur bord, le tore $\mathbb{S}^1 \times \mathbb{S}^1$.
$$ $$
Nous allons voir qu’en général toute variété de dimension 3 peut être obtenue par recollement successifs d’anses, à savoir quatre types de pièces comme dans l’animation ci-dessous, dans laquelle on montre une boule (ou anse d’indice $0$, ou encore 0-anse), deux cylindres pleins (ou 1-anses), deux disques épaissis (ou 2-anses) et encore une boule (ou 3-anse).
Le lecteur scrupuleux cherchera sans-doute ce qui différencie fondamentalement un cylindre plein d’un disque épaissi, et à plus forte raison une boule d’une autre boule, et se demandera donc la différence entre $1$ et $2$-anses d’une part, et entre $0$ et $3$-anses d’autre part. Mieux ou pire : à homéomorphisme près, toutes ces « pièces » sont les mêmes, et les variétés qu’on obtient en recollant de telles pièces ne sont définies qu’à homéomorphisme près, donc pourquoi donner des noms différents à ces pièces en apparence identique ? C’est parce qu’en fait, strictement parlant, ce n’est pas l’anse qui est d’indice $k$, mais l’opération d’attachement d’anse. L’indice indique quelle partie du bord de la pièce (vert foncé dans l’animation ci-dessus) doit être recollée à la variété à bord précédente, le reste (en vert clair), devenant une partie du bord de la nouvelle variété obtenue [1].
On commence par visualiser le recollement de 1-anses sur une 0-anse.
Corps en anses
Recoller les 1-anses à la 0-anse donne une « bouée pleine à $g$ places », autrement appelé corps en anses de genre $g$ :
On appelle corps en anses de genre $g$ la [2] variété à bord de dimension 3 obtenue à partir d’une boule (ou 0-anse) en lui attachant $g$ cylindres (ou 1-anses) $\mathbb{D}^2 \times [-1 , 1]$. On demande de plus que l’homéomorphisme de recollement identifie les $2g$ disques $\mathbb{D}^2 \times \{ \pm 1 \}$ avec $2g$ disques disjoints dans le bord de la boule de telle sorte que la variété ainsi obtenue soit orientable.
L’animation suivant montre comment recoller deux 1-anses sur une 0-anse pour obtenir un corps en anses de genre 2.
À l’issu du recollement on obtient donc un corps en anses de genre 2 :
Suivant Heegaard (et Poincaré dans le cinquième complément à l’Analysis Situs) on symbolise ce dernier par un diagramme comme le montre l’animation suivante.
Scindement de Heegaard
Il se trouve que toute variété de dimension 3, compacte, sans bord et orientable $V$ peut être obtenue en recollant deux corps en anses, nécessairement de même genre $g$, selon leur bord. Une telle décomposition est appelée scindement de Heegaard de $V$, de genre $g$.
Toute variété de dimension 3, compacte, sans bord et orientable admet un scindement de Heegaard.
Démonstration. Notons $V$ la variété et fixons une triangulation $T$ de $V$. On associe à $T$ un scindement de Heegaard de $V$ comme suit. On remplace chaque sommet de $T$ par une boule (ou 0-anse), chaque arête par un cylindre (ou 1-anse), chaque face d’un tétraèdre par un disque épaissi (ou 2-anse) et chaque tétraèdre par une boule (ou 3-anse), comme on le montre l’animation suivante.
La réunion des 0- et 1-anses forme un premier corps en anses. Et la réunion des 2- et 3-anses forme le deuxième corps en anses. [3]
C.Q.F.D.
$$ $$
Étant donné une scindement de Heegaard $V= H_g \cup H_g '$ de genre $g$, on peut facilement construire un autre scindement de Heegaard de $V$ de genre $g+1$ en ajoutant une 1-anse non nouée à $H_g$ pour obtenir un corps en anses $H_{g+1}$ de genre $g+1$. Ici, on dit que la 1-anse est non nouée s’il existe un disque $D$ dans $V$ tel que $D \cap H_{g+1} = \partial D$ et la courbe $\partial D$ ne parcourt la 1-anse qu’une seule fois, comme la courbe rouge dans l’animation Élimination d’une 1-anse (et d’une 2-anse complémentaire).
On peut alors épaissir le disque $D$ en une 2-anse $C = D \times I$. La réunion $B \cup C$ étant homéomorphe à une boule, on a :
$$V \cong H_g \cup (B \cup C) \cup H_g ' = (H_g \cup B) \cup (C \cup H_g '),$$
où $H_g \cup B = H_{g+1}$. La 2-anse $C$ intersectant le corps en anses $H_g '$ selon deux disques, la réunion $C \cup H_g '$ est un corps en anses $H_{g+1} '$ de genre $g+1$ et $V = H_{g+1} \cup H_{g+1} '$ est un scindement de Heegaard de genre $g+1$.
L’opération que l’on vient de décrire est appelé stabilisation. Par exemple, le scindement de genre 1 de $\mathbb{S}^3$ décrit ci-dessus peut être obtenu par stabilisation du scindement de genre 0.
Deux scindements de Heegaard d’une variété $V$ sont dits équivalents s’il existe un homéomorphisme de $V$ dans lui-même qui envoie un scindement sur l’autre. Ils sont dits stablement équivalents s’ils sont équivalents après avoir appliqué un certain nombre de stabilisations à chacun d’entre eux.
Le résultat suivant est dû à Singer [4] et Reidemeister [5].
Deux scindements de Heegaard d’une variété de dimension 3, compacte, sans bord et orientable sont stablement équivalents.
$$ $$
On appelle genre d’une variété $V$ de dimension 3, compacte, sans bord et orientable le plus petit entier $g$ tel que $V$ admette un scindement de Heegaard de genre $g$.
On peut préférer recoller inductivement les anses, en commençant par recoller les 1-anses sur les 0-anses comme expliqué ci-dessus, puis les 2-anses sur le premier corps en anses et finalement les 3-anses. On parle alors de décomposition en anses. Une décomposition en anses est un scindement de Heegaard de genre $g$ si elle consiste en une 0-anse, $g$ 1-anses et 2-anses et une 3-anse. Le recollement des 1-anses à la 0-anse donne un premier corps en anses de genre $g$. Et le recollement des 2-anses à la 3-anse donnent le deuxième corps en anses. L’espace total est donc la réunion de ces deux corps en anses le long de leur bords (deux surfaces de genre $g$). On détaille ici comment associer une décomposition en anses à une variété polyédrique.
Expliquons maintenant comment « coder » une décomposition en anses par un diagramme qui fera office de « plan de construction » de la variété.
Diagramme de Heegaard
On a déjà expliqué comment indiquer où recoller les 1-anses sur une 0-anse. Il faut maintenant expliquer comment recoller les pièces suivantes, à savoir les disques épaissis ou 2-anses, sur le premier corps en anses. Pour cela on trace des courbes simples fermées sur le corps en anses, courbes qui indiquent comment recoller les 2-anses.
L’espace total étant une variété, après recollement des 2-anses la variété à bord obtenue a pour bord une réunion disjointe de sphères selon lesquelles on peut recoller les 3-anses (boules) :
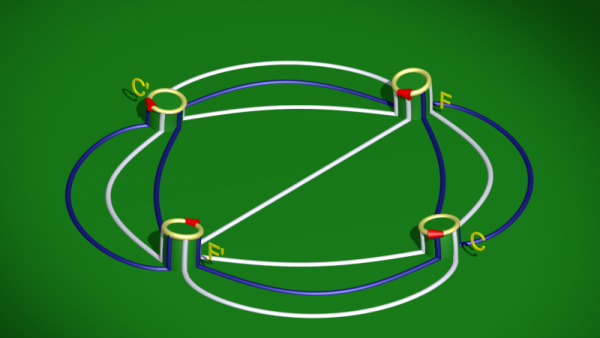
Finalement on code toutes ces données dans un diagramme :
Dans ce diagramme les flèches rouges indiquent non seulement comment identifier les cercles C et C’ ou F et F’ pour former des anses mais aussi, en suivant l’ordre cyclique de point initial (et dirigé par) la flèche, comment identifier les arcs bleus et blancs pour former des courbes simples fermées sur le corps en anses. Le diagramme détermine complètement une décomposition en corps en anses.
On appelle diagramme de Heegaard de genre $g$ un diagramme associé comme ci-dessus à un scindement de Heegaard. Un tel diagramme est constitué de deux systèmes de courbes simples fermées sur une surface orientable fermée $S$ de genre $g$. On demande en outre que les courbes de ces deux systèmes vérifient les conditions suivantes :
- le nombre de courbes dans chaque système est $g$ ;
- les courbes de chaque système sont disjointes ;
- le résultat du découpage de la surface $S$ selon chacun de ces systèmes de courbes est une surface connexe (une sphère privée de $2g$ disques ouverts).
Un diagramme de Heegaard détermine la variété qu’il permet de reconstruire : il correspond en effet à tout diagramme de Heegaard un scindement de Heegaard dans lequel les courbes de chaque système forment un système complet de méridiens de l’un des deux corps en anses de la décomposition. Après recollement des 2-anses la variété à bord obtenue a pour bord une sphère. Il reste à lui recoller une 3-anse (boule) mais un théorème de Smale assure que tout difféomorphisme de la sphère $\mathbb{S}^2$ préservant l’orientation est isotope à l’identité. Et un lemme de recollement implique encore que l’espace obtenu est uniquement déterminé. On étudie plus particulièrement l’exemple des variétés lenticulaires qui sont précisément les variétés de genre 1.
À une même variété correspond une infinité de diagrammes de Heegaard, on décrit ici plusieurs opérations élémentaires sur les diagrammes de Heegaard qui ne modifient pas la variété associée.
Si l’on supprime les conditions 1 et 3 dans la définition ci-dessus et qu’on se contente de demander que le résultat du découpage de la surface $S$ selon chaque système de courbes est une réunion de sphères privées de disques ouverts, il correspond encore au diagramme une décomposition en anses. On parle alors de diagramme de Heegaard généralisé.
[2] Le fait que cette variété soit uniquement déterminée à difféomorphisme près découle du deuxième lemme de recollement.
[3] Qui est aussi l’épaississement du 1-squelette de la cellulation duale de $V$.
[4] J. Singer, Three dimensional manifolds and their Heegaard diagrams, Trans. Amer. Math. Soc. 35 (1933), 88-111.
[5] K. Reidemeister, Zur dreidimensional Topologie, Abh. Math. Ses. Unis. Hamburg 9 (1933), 189-194.