|
> Triangulation des variétés > Cellulation duale à une triangulation lisse d’une variété Cellulation duale à une triangulation lisse d’une variété |
Nous définissons ici la cellulation duale à une triangulation lisse d’une variété. Cet objet est la source géométrique de la dualité de Poincaré. Le point de départ en est la subdivision barycentrique de la triangulation de départ.
Soient $V$ une variété lisse compacte de dimension $d$ et $(X,f)$ une cellulation lisse de $V$. Puisque $V$ est compacte, le polyèdre $X$ est fini. Soit $K$ une triangulation de $X$. On note $K'$ la première subdivision barycentrique de $K$. Les sommets de $K'$ sont donc les barycentres des simplexes $K$. Plus précisément, pour chaque simplexe $\sigma$ de $K$, on notera $\hat{\sigma}$ son barycentre.
Les sommets de $K'$ sont naturellement ordonnés par l’inclusion des faces correspondantes de $K$, autrement dit $\hat{\sigma} < \hat{\tau}$ si $\sigma$ est face une strictement incluse dans $\tau$.
Soit $\sigma$ un $i$-simplexe de $K$. La subdivision $K'$ de $K$ induit une subdivision de $\sigma$ formée de la réunion de tous les simplexes de $K'$ de sommets $a_0 a_1 \ldots a_i$ avec $a_0 < a_1 < \ldots < a_i$ et $a_i = \hat{\sigma}$ (et de leurs sous-simplexes).
Soit $\sigma$ une cellule de dimension $i$ de $K$. On appelle bloc dual à $\sigma$ la réunion $\sigma^*$ de tous les simplexes $b_0 b_1 \ldots b_{\ell}$ de $K'$ avec $b_0 = \hat{\sigma}$ et $b_0 < b_1 < \ldots < b_\ell$ (et leurs sous-simplexes).
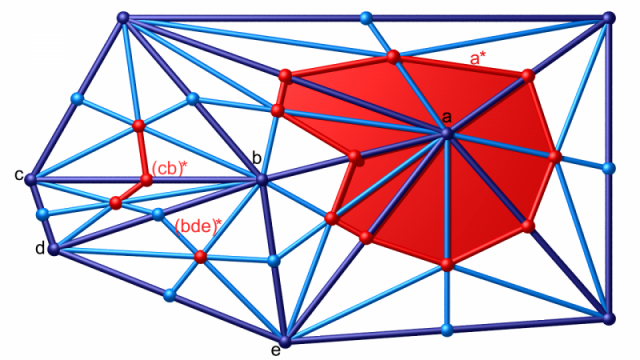
Dans la figure ci-dessous, on a représenté une triangulation $K$ en bleu foncé, et la première subdivision barycentrique de $K$ en bleu plus clair. Les blocs duaux au sommet $a$, à l’arête $(bc)$ et au triangle $(bde)$ sont en rouge.
Noter que $|\sigma^*|$ est PL-isomorphe à $[-1,1]^{d-i}$ puisqu’il est PL-isomorphe au cône de sommet $\hat{\sigma}$ sur le link de $\sigma$ dans $K$. [1]
La réunion des blocs $\sigma^*$ est la réalisation d’un complexe (dont les cellules sont des unions de cellules $K'$) que l’on note $K^*$. Il correspond à ce complexe une cellulation lisse $(K^* , f^*)$ de la variété $V$ ; on appelle $(K^* , f^*)$ le cellulation duale à la triangulation lisse $(K,f)$ de $V$. On identifie alors le complexe $K'$ à une subdivision du complexe $K^*$.
Notons que les cellules de dimension $i$ de $K^*$ correspondent aux cellules de dimension $d-i$ de $K$. L’existence des deux cellulations « duales » $(K,f)$ et $(K^* , f^*)$ de la (même) variété $V$ est la source géométrique de la dualité de Poincaré.
[1] C’est ici qu’il est fondamental que $V$ soit un variété. On peut en effet toujours définir un complexe dual $K^*$ comme ci-dessus mais si les $|\sigma^*|$ ne sont pas des cellules, l’« homologie » de $K^*$ calculée à partir de la décomposition de $K^*$ en $\sigma^*$ n’est pas isomorphe en général à l’homologie de $|K^*|$.