|
> Triangulation des variétés > Polyèdres, applications et variétés PL Polyèdres, applications et variétés PL |
Les polyèdres sont des objets vivant dans un espace affine. On définit entre les polyèdres la classe des applications PL, ce qui mène à la définition des variétés PL. Nous présentons ces constructions dans cet article.
Grâce au théorème de Whitehead, nous verrons que toute variété lisse est munie d’une unique structure de variété PL compatible. Cette structure permet de calculer l’homologie d’une variété grâce à l’homologie polyèdrale.
Dans cet article, on présente une catégorie d’objets rigides vivant dans un espace affine, les polyèdres, entre lesquels on peut définir la classe particulière des applications PL, ce qui mène tout naturellement à la notion de variété PL. Une telle variété est, par définition, munie d’une classe privilégiée de cellulations linéaires. [1]
Complexes cellulaires affines
Une cellule linéaire $D$ dans un espace euclidien $\mathbb{R}^n$ est l’enveloppe convexe d’un nombre fini de points de $\mathbb{R}^n$. En particulier $D$ est un sous-ensemble convexe et compact de $\mathbb{R}^n$. On appelle intérieur (formel) d’une cellule $D$, et l’on note $\mathrm{int}(D)$, l’intérieur topologique de $D$ dans le sous-espace affine $\mathrm{Aff}(D)$ de $\mathbb{R}^n$ qu’elle engendre. Le bord (formel) de $D$, noté $\partial D$, est son bord topologique dans $\mathrm{Aff}(D)$, c’est-à-dire le sous-ensemble $D - \mathrm{int} (D)$. La dimension de $D$, notée $\mathrm{dim}(D)$, est la dimension de $\mathrm{Aff}(D)$.
Une famille importante de cellules linéaires est constituée des simplexes (linéaires). Rappelons qu’un simplexe $\sigma$ de dimension $r$ dans un espace euclidien $\mathbb{R}^n$, pour un certain $n \geq r$, est l’enveloppe convexe de $r+1$ points indépendants [2] $s_0 , \ldots s_r$. Les $s_i$ sont les sommets de $\sigma$. Les faces de $\sigma$ sont les simplexes de dimension $r-1$ dont les sommets sont des sommets de $\sigma$.
Un complexe dans un espace euclidien $\mathbb{R}^n$ est un ensemble $K$ de cellules linéaires dans $\mathbb{R}^n$ tel que :
- si $D$ et $D'$ sont deux cellules distinctes appartenant à $K$, alors les intérieurs $\mathrm{int}(D)$ et $\mathrm{int}(D')$ sont disjoints ;
- si $D \in K$, le bord formel $\partial D \subset \mathbb{R}^n$ est réunion d’autres cellules de $K$ ;
- si $x \in D \in K$, il existe un voisinage $U$ de $x$ dans $\mathbb{R}^n$ tel que $U$ ne rencontre qu’un nombre fini de cellules de $K$ [3].
La dernière condition est une condition de finitude locale ; dans la plupart des exemples l’ensemble $K$ lui-même sera fini. La dimension maximale d’une cellule de $K$ est appelée dimension de $K$. On appelle sous-complexe de $K$ tout complexe constitué de cellules de $K$.
Étant donné une cellule $D \in K$ on appelle hyperface de $D$ toute cellule linéaire de dimension $\mathrm{dim}(D)-1$ dans $K$ et contenue dans $\partial D$. Enfin une face de $D$ est une intersection d’hyperfaces de $D$ (donc en particulier une cellule linéaire). Une face de dimension $0$ est un sommet, et une face de dimension $1$ une arête.
Un complexe $K$ est dit simplicial si toute cellule $D \in K$ est un simplexe et si chaque cellule $D' \subset D$ constitue une face entière du simplexe $D$.
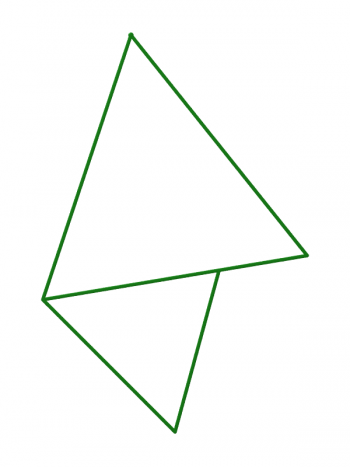
Voici un complexe dont toute cellule est un simplexe mais qui n’est pas simplicial :
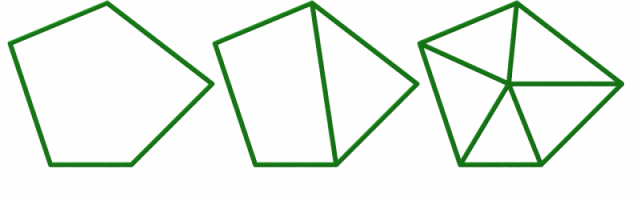
Soit $K$ un complexe et $D$ une cellule de $K$. On appelle étoile de $D$ dans $K$ le sous-complexe $\mbox{ét} (D,K)$ réunion des cellules de $K$ qui contiennent $D$.
Dans un complexe simplicial, on appelle link d’un simplexe $D \in K$ le sous-complexe $\mathrm{lk} (D,K)$ réunion des simplexes de $\mbox{ét} (D,K)$ qui sont disjoints de $D$.
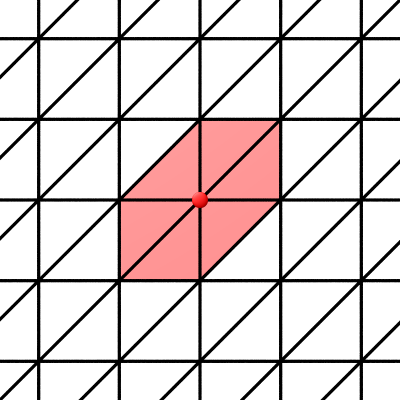
Une cellule de dimension $0$ (le sommet rouge) et son étoile (les cellules de dimensions $0$, $1$ et $2$ situées dans la zone rosée) :
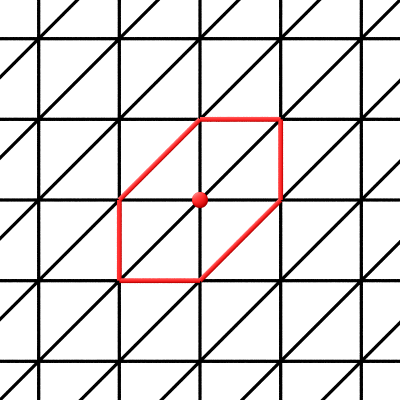
La même cellule de dimension $0$ et son link (les sommets et arêtes du polygone rouge) :
Polyèdres et leurs cellulations
Notre véritable objet d’intérêt n’est pas le complexe lui-même, mais l’espace topologique sous-jacent :
On appelle polyèdre associé à un complexe $K$ — ou réalisation de $K$ — la réunion $|K|$ de ses cellules :
$$|K| = \bigcup_{D \in K } D$$
que l’on munit de la topologie induite par celle de l’espace euclidien ambiant. On appelle plus généralement polyèdre toute partie d’un espace euclidien qui est la réalisation d’un complexe (non précisé).
Une conséquence de la condition de finitude locale est qu’un complexe $K$ est fini si et seulement si le polyèdre associé $|K|$ est compact.
On appelle cellulation (linéaire) d’un polyèdre $X$ la donnée d’un complexe $K$ tel que $X=|K|$. Si de plus $K$ est simplicial, on parlera de triangulation. On dit qu’une cellulation $K'$ d’un polyèdre $X$ est une subdivision d’une autre $K$, et on écrit $K' < K$, si chaque cellule $D' \in K'$ est contenue dans une cellule $D \in K$.
Soit $K$ est un complexe simplicial. Un exemple important de subdivision est celui de la première subdivision barycentrique $K' < K$ représentée ci-dessous. Les sommets de $K'$ sont les barycentres $\hat{D}$ des simplexes $D \in K$. Des sommets $\hat{D}_0 , \ldots , \hat{D}_p$ engendrent un simplexe de $K'$ si et seulement si chaque $D_i$ est une face (stricte et non vide) de $D_{i+1}$.
Si un polyèdre n’est pas naturellement muni d’une cellulation particulière (il en possède en fait une infinité), le lemme suivant affirme que ce sont toutes « les mêmes », à subdivision près.
Soient $K_1$ et $K_2$ deux complexes tels que $|K_1| = |K_2|$. Alors il existe une subdivision commune $K_0$, c’est-à-dire $K_0 < K_1$ et $K_0 < K_2$.
Démonstration. Il suffit d’intersecter les deux cellulations.
C.Q.F.D.
Par exemple l’espace euclidien $\mathbb{R}^n$ est naturellement un polyèdre : on peut considérer la cellulation dont les cellules sont les translatés par un vecteur de $\mathbb{Z}^n$ du cube $[0,1]^n$ et de toutes ses faces. Et cette structure de polyèdre est canonique dans le sens où deux cellulations de $\mathbb{R}^n$ sont toujours compatibles.
Noter que le monde des complexes est plus flexible que celui des complexes simpliciaux comme le montre le fait élémentaire suivant.
Étant donné un complexe $K$ et un sous-complexe $L$, toute subdivision de $L$ induit canoniquement une subdivision de $K$ qui laisse intacte toute cellule de $K$ qui n’est pas dans $L$.
Toute cellulation $K$ d’un polyèdre $X$ admet une subdivision $K' < K$ qui est une triangulation.
Démonstration. On procède par récurrence sur la dimension de $K$. Un complexe de dimension $0$ ou $1$ est toujours simplicial. Supposons maintenant que tout complexe de dimension $k$, pour un certain $k\ge 1$, admet une subdivision qui est une triangulation, et considérons un complexe de dimension $k+1$. Son $k$-squelette, c’est-à-dire l’union de toutes ses cellules de dimension inférieure ou égale à $k$, admet une subdivision simpliciale par hypothèse de récurrence, qui, d’après le fait ci-dessus, induit une subdivision de $K$. On subdivise alors chaque cellule de dimension $k+1$ en prenant les cônes depuis un point de son intérieur sur chacune des cellules du bord. Le cône sur chacun de ces simplexes est encore un simplexe. Ainsi, la subdivision de $K$ obtenue est une triangulation.
C.Q.F.D.
$$ $$
Il est parfois utile de considérer des subdivisions particulières. Cela motive la définition suivante due à Larry Siebenmann.
Soit $X \subset \mathbb{R}^n$ un polyèdre muni d’une cellulation $K$. On dit qu’une cellulation $K'$ de $X$ résulte d’une bisection (linéaire) de $K$ en $D \in K$, et on écrit $K \to K'$, si on peut former $K'$ en remplaçant $D \in K$ par trois cellules $D_-$, $D_+$, $D_0$, où $D_0$ est l’intersection transverse d’un hyperplan de $\mathbb{R}^n$ avec $D$ et découpe $D$ en deux cellules non vides $D_-$ et $D_+$.
On écrit $K' \prec K$, s’il existe une suite finie de bisections
$$K=K_1 \to K_2 \to \ldots \to K_n = K',$$
et on dit que $K'$ se déduit de $K$ par bisections.
Voici un exemple de bisection :
Ci-dessous, une cellulation triviale d’un pentagone, et deux subdivisions de cette cellulation. La subdivision du milieu résulte d’une bisection, mais pas celle de droite (ni même d’une suite de bisections) :
Noter que $K' \prec K$ entraîne $K' < K$ mais que la réciproque est fausse. Elle est néanmoins vraie à « re-subdivision par bisections près », ce qui est un cas particulier, mais aussi le cœur de la preuve de la proposition suivante, qui renforce le lemme de compatibilité des cellulations.
Soit $X$ un polyèdre compact et $K_1$, $K_2$ deux cellulations de $X$. Alors il existe une cellulation $K_0$ de $X$ qui est une subdivision par bisections de $K_1$ et $K_2$, c’est-à-dire $K_0 \prec K_1$ et $K_0 \prec K_2$.
Démonstration. Commençons par considérer le cas où $K_1 < K_2$. Grâce au fait ci-dessus, on peut procéder cellule par cellule indépendamment, ce qui nous ramène au cas où $K_2$ est constitué d’une unique cellule $D$ de dimension $n$ et des cellules de son bord. Maintenant il existe une famille finie $H_1 , \ldots , H_k$ d’hyperplans de $\mathbb{R}^n$ tels que toute cellule de $K_1$ soit une intersection finie de demi-espaces associés aux $H_i$. Chaque $H_i$ induit une subdivision par bisections de $K_2$, mais aussi de $K_1$ [4]. Le résultat final commun de ces subdivisions par bisections est la cellulation $K_0$ recherchée.
Voyons maintenant comment le cas général se déduit du cas particulier ci-dessus. Soient $K_1$ et $K_2$ deux cellulations d’un même polyèdre $X$. On sait déjà qu’elles admettent une subdivision commune $K'$. D’après ce qui précède, $K'$ et $K_1$ admettent une subdivision par bisections commune $K''$. Mais alors $K'' < K'$ et $K' < K_2$ donc $K''$ est aussi une subdivision de $K_2$, et on peut à nouveau appliquer le cas particulier ci-dessus pour obtenir une subdivision par bisections commune $K_0$ de $K''$ et $K_2$, mais aussi de $K_1$ puisque $K''\prec K_1$.
C.Q.F.D.
Partant d’un polyèdre triangulé $X=|K|$ et passant à une suite $(K_i)$ de subdivisions simpliciales fine, c’est-à-dire telle que le diamètre des simplexes de $K_i$ tend vers zéro lorsque $i \to \infty$, on montre facilement le lemme suivant.
Tout ouvert d’un polyèdre $X \subset \mathbb{R}^n$ est encore un polyèdre.
Applications et variétés PL
Soit $X \subset \mathbb{R}^n$ un polyèdre. Une application $f: X \to \mathbb{R}^m$ est PL s’il existe une cellulation $K$ de $X$ telle que la restriction de $f$ à toute cellule $D \in K$ soit égale à la restriction d’une application affine $\mathbb{R}^n \to \mathbb{R}^m$.
Si $X \subset \mathbb{R}^n$ et $Y \subset \mathbb{R}^m$ sont deux polyèdres, une application $f:X \to Y$ est PL si l’application sous-jacente $X \to \mathbb{R}^m$ est PL.
Soit $f:X \to Y$ un homéomorphisme PL entre deux polyèdres. Alors l’application inverse $f^{-1} : Y \to X$ est encore PL.
Démonstration. Soit $K$ une cellulation de $X$ telle que la restriction de $f$ à toute cellule $D \in K$ soit affine. L’image de $K$ par $f$ est une cellulation $L$ de $Y$ et la restriction de $f^{-1}$ à chaque cellule de $L$ est affine.
C.Q.F.D.
Montrer que deux cellules linéaires de même dimension (et a fortiori leurs bords) sont PL-homéomorphes.
On peut voir ce fait comme un cas très particulier d’un résultat beaucoup plus général, le Théorème de Whitehead sur la compatibilité des cellulations lisses des variétés.
Soit $V$ un polyèdre. On dit que $V$ est une variété PL (de dimension $n$) si, pour tout point $x \in V$, il existe un ouvert $U \subset V$ contenant $x$ et un homéomorphisme PL entre $U$ et $\mathbb{R}^n$.
Cette définition n’est pas standard, elle correspond plutôt à la notion de « sous-variété PL de $\mathbb{R}^n$ ». Une variété PL désigne plus couramment une variété topologique munie d’un atlas dont les changements de cartes sont des homéomorphismes PL au sens ci-dessus. De la même manière qu’une variété lisse (séparable) peut être réalisée comme une sous-variété lisse d’un $\mathbb{R}^n$, une variété PL (séparable) en ce sens plus standard peut être réalisée (via un homéomorphisme PL) comme une variété PL au sens de notre définition. La preuve de ce résultat repose, comme la partie « facile » du théorème de Whitehead, sur un Lemme de recollement de plongements compatibles. Nous avons délibérément préféré mettre en avant l’objet rigide qu’est un polyèdre plutôt qu’une classe de tels objets.
Soit $X \subset \mathbb{R}^n$ un polyèdre, $x$ un point de $X$, et $K,L$ deux triangulations de $X$ dont $x$ est un sommet [5], alors il existe des homéomorphismes PL :
$$|\mbox{ét} (x, K)| \cong |\mbox{ét} (x, L)| \quad \mbox{et} \quad |\mathrm{lk} (x,K)| \cong |\mathrm{lk} (x,L)|. $$
Démonstration. On se ramène au cas où $L$ est une subdivision simpliciale de $K$. Soient $D_i$ les simplexes de $\mathrm{lk} (x, L)$ et soient $D_i^+$ les cônes positifs infinis sur $D_i$ depuis $x$. Alors les intersections $D_i^+ \cap A$, où $A$ parcourt les simplexes du link $\mathrm{lk} (x, K)$, forment une subdivision simpliciale $M$ de $\mathrm{lk}(x, K)$. Finalement la projection radiale $|\mathrm{lk} (x, L)| \to |M|$ est un homéomorphisme PL. Le cas de l’étoile s’en déduit.
C.Q.F.D.
Par abus de langage on notera $\mbox{ét} (x)$, resp. $\mathrm{lk} (x)$, la classe de polyèdres, considérés à homéomorphismes PL près, ainsi obtenus. Noter que $\mbox{ét} (x)$ et $\mathrm{lk} (x)$ ne dépendent que d’un voisinage arbirtrairement petit de $x$ dans $X$.
Un polyèdre $X$ est une variété PL si et seulement si pour tout $x \in X$, le link $\mathrm{lk} (x)$ est PL-homéomorphe à la sphère $\mathbb{S}^{n-1}$ (que l’on voit comme un polyèdre via son identification au bord d’un simplexe de dimension $n$).
Ainsi, l’espace construit par Poincaré dans son deuxième exemple de recollement du cube, dont on montre ici qu’il peut-être réalisé comme un polyèdre, n’est pas une variété PL. En effet, dans ce polyèdre, les links des images des sommets du cubes sont des tores.
Notons qu’on aurait pu identifier la sphère au bord de n’importe quelle cellule linéaire de dimension $n$ sans changer la proposition, puisque l’on a vu en exercice que les bords de deux telles cellules étaient PL-homéomorphes. Plus généralement, d’après le Théorème de Whitehead, à toute variété lisse est canoniquement associée toute une classe de polyèdres homéomorphes à cette variété et PL-homéomorphes entre eux.
Démonstration de la proposition. Si $X=\mathbb{R}^n$ et $x\in X$ est l’origine, alors le link $\mathrm{lk}(x)$ est bien PL-homéomorphe à la sphère $\mathbb{S}^{n-1}$ (cf. Exercice). Le sens direct est donc immédiat. Réciproquement, soit $X$ un polyèdre et $x$ un point de $X$ dont le link $\mathrm{lk} (x)$ est PL-homéomorphe à la sphère $\mathbb{S}^{n-1}$. Il existe une triangulation $K$ de $X$ telle que $x$ soit un sommet de $K$. Alors l’étoile $\mbox{ét} (x,K)$ peut être identifiée au cône sur le link $\mathrm{lk} (x,K)$. En particulier $x$ a un voisinage qui est PL-homéomorphe à un disque ouvert dans $\mathbb{R}^n$.
C.Q.F.D.
Une variété PL est naturellement une variété topologique. On peut d’ailleurs penser à une variété PL comme à une variété topologique munie d’une classe particulière de triangulations. On prendra toutefois garde au fait qu’il existe des polyèdres homéomorphes à des variétés mais qui ne sont pas des variétés PL. En voici un exemple, dû à Cannon [6]. À la sphère d’homologie de Poincaré $P$ est naturellement associée, en tant que variété lisse, une classe particulière de complexes simpliciaux dont les réalisations sont homéomorphes à $P$ (cf. Théorème de Whitehead). La double suspension $\Sigma^2 X$ de l’un quelconque de ces polyèdres est un polyèdre homéomorphe à la sphère $\mathbb{S}^{5}$ (c’est là le résultat de Cannon), mais n’est pas une variété PL : deux de ses points ont pour link la (simple) suspension $\Sigma X$, qui n’est même pas une variété, deux de ses points à elle ayant pour link $X$, qui n’est pas homéomorphe à une sphère. Enfin, on peut également montrer qu’il existe des variétés topologiques qui ne sont homéomorphes à aucun polyèdre [7]. On montre toutefois ici que la situation est bien plus simple pour les variétés lisses.
[1] On devrait plutôt dire affines comme nous le ferons parfois dans la suite, mais le terme PL est maintenant standard.
[2] C’est-à-dire que les vecteurs $v_1=s_1-s_0 , \ldots , v_r= s_r-s_0$ sont linéairement indépendants.
[3] Cette dernière condition entraîne en particulier que le bord formel d’une cellule de $K$ est réunion d’un nombre fini d’autres cellules de $K$.
[4] Noter le pluriel de ``bisections" : en toute rigueur, la subdivision de $K_j$ induite par $H_i$ résulte d’une suite de bisections affectant tour à tour les cellules de $K_j$ par ordre de dimension croissante.
[5] On notera que, si $x$ est un point quelconque d’un polyèdre $X$, on peut toujours trouver une cellulation (et par suite, une triangulation) de $X$ dont $x$ est un sommet.
[6] J. W. Cannon, Shrinking cell-like decompositions of manifolds. Codimension three, Ann. of Math. (2), 110, 1979, 83—112.
[7] Relativement à cette question les résultats les plus définitifs sont dus à Ciprian Manolescu, voir en particulier le Théorème 4 de la page 3 de son article Triangulations of manifolds.