
|
> Exemples de dimension 3 > Topologie des variétés de dimension 3 > Chirurgie de Dehn Chirurgie de Dehn |
Soit $k$ un nœud dans une variété $V$ de dimension 3 compacte, orientable et sans bord. En ôtant un voisinage tubulaire $N(k)$ de $k$, on obtient deux variétés à bord :
- l’extérieur du nœud $K=V \setminus \mathrm{int} \ N(k)$ ;
- le tore solide $N(k)$ que nous identifions au tore solide standard $\mathbb{D}^2 \times \mathbb{S}^1$.
La variété $K$ est donc une variété de bord $\partial K = \mathbb{T}^2$ et on a
$$V = K \cup ( \mathbb{D}^2 \times \mathbb{S}^1 ).$$
On peut plus généralement recoller $K$ et $\mathbb{D}^2 \times \mathbb{S}^1$ à l’aide d’un homéomorphisme quelconque
$$h : \partial \mathbb{D}^2 \times \mathbb{S}^1 \to \partial K .$$
L’espace
$$Q = K \cup_h (\mathbb{D}^2 \times \mathbb{S}^1 )$$
que l’on obtient ainsi est encore une variété de dimension 3 compacte, orientable et sans bord. On dit que la variété $Q$ est obtenue à partir de $V$ par chirurgie le long de $k$.
Chirurgie dans $\mathbb{S}^3$
La variété $Q$ ci-dessus dépend du choix de l’homéomorphisme $h$. En fait le deuxième lemme de recollement assure que la variété $Q$ est complètement déterminée par l’image par $h$ d’un méridien $\partial \mathbb{D}^2 \times \{ * \}$ du tore solide $\mathbb{D}^2 \times \mathbb{S}^1$, c’est-à-dire par la courbe $\gamma = h (\partial \mathbb{D}^2 \times \{ * \} )$ sur le bord de $K$.
Fixons une courbe simple fermée
$$\gamma \subset \partial K = \mathbb{T}^2.$$
Il s’agit de montrer que la classe d’isotopie de $\gamma$ détermine complètement la variété $Q$. Soit $A$ un voisinage régulier de $\gamma$ dans $\mathbb{T}^2$. Pour reconstruire $Q$ on peut commencer par recoller un disque épaissi (ou 2-anse) $D^2\times[0,1]$ le long de $A$ : on identifie le bord $\mathbb{S}^1\times[0,1]$ du disque épaissi avec $A$. Le lemme de recollement assure que la variété obtenue ne dépend que de la classe d’isotopie de la courbe $\gamma$. Cette variété a encore un bord, homéomorphe à une sphère de dimension 2. En bouchant ce bord avec une boule (3-anse), on obtient une variété fermée. Une deuxième application du deuxième lemme de recollement assure encore que le résultat ne dépend pas de l’identification choisie entre la sphère de bord et le bord de la boule, car tout homéomorphisme de $\mathbb{S}^2$ qui préserve l’orientation est isotope à l’identité.
$$ $$
De manière à insister sur la dépendance en la (classe d’isotopie de la) courbe $\gamma$, dans la suite on note $K (\gamma )$ la variété $Q$.
Si $V= \mathbb{S}^3$ une courbe simple fermée $\gamma$ dans $\partial K$ est complètement déterminée, à isotopie près, par un couple $(p,q)$ d’entiers premiers entre eux. Détaillons cette correspondance. En général, le nœud $k$ n’étant pas trivial, son extérieur $K$ est une variété plutôt compliquée, mais du point de vue homologique, elle se comporte comme un tore solide :
Pour tout $i$ on a $H_i(K ) \cong H_i (\mathbb{D}^2\times\mathbb{S}^1)$, autrement dit
$$H_0 (K) = H_1 (K) = \mathbb{Z} \mbox{ et } H_i (K) = 0 \mbox{ si } i \geq 2.$$
Cette proposition est un cas particulier de la dualité d’Alexander. On peut également la déduire de la suite exacte longue de Mayer-Vietoris, une fois connues l’homologie du tore solide et de la 3-sphère.
$$ $$
Le bord $\partial K$ est un tore $\mathbb{T}^2$ sur lequel nous fixons deux courbes simples fermées qui forment une base de l’homologie : un méridien $m$, à savoir une courbe qui borde un disque dans $N(k)$, qui représente un générateur de $H_1 (K)$, et une longitude. À isotopie près, il existe une unique longitude dont la classe d’homologie dans $H_1 (K)$ est triviale, cela détermine une deuxième courbe $\ell$ ; c’est aussi une courbe qui borde une surface de Seifert dans $K$. Ces deux courbes forment une base de $H_1 (\mathbb{T}^2 )$ et le couple $(m, \ell)$ est unique à isotopie et au renversement des orientations près [1]. On fixe les orientations comme suit. L’orientation standard de $\mathbb{S}^3$ induit une orientation de $K$. Notons $n$ le vecteur normal au bord de $K$ pointant vers l’intérieur de $K$. On fixe les orientations des courbes $m$ et $\ell$ de sorte que le triplet $(m, \ell , n)$ soit orienté positivement, comme sur la figure ci-dessous.
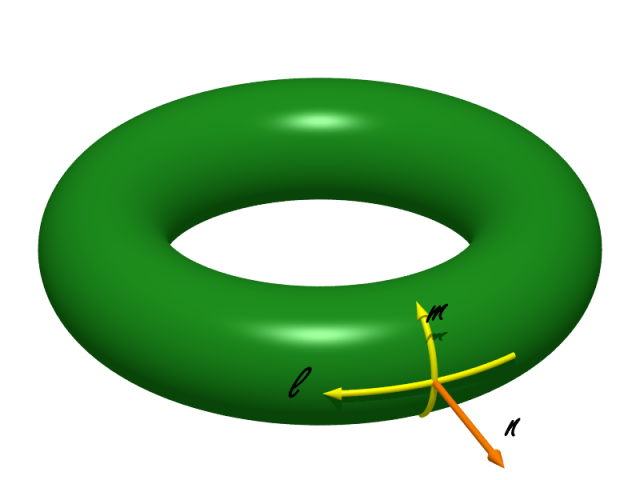
Dans le revêtement universel de $\mathbb{T}^2$, qui est un plan, $m$ et $\ell$ se relèvent en deux familles de droites parallèles. Identifions une composante connexe des relevés de $m$ avec l’axe des $y$ et une composante des relevés de $\ell$ avec l’axe des $x$. À isotopie près, toute courbe simple fermée $\gamma$ se relève dans le revêtement universel de $\mathbb{T}^2$ en une famille de droites parallèles de pente rationnelle (éventuellement infinie). Toujours à isotopie près, on peut supposer que l’une de ces droites passe par $(0,0)$. On peut donc choisir la courbe de chirurgie $\gamma$ de la forme $p m+q \ell$, avec $p$ et $q$ des entiers premiers entre eux. Les couples $(p,q)$ et $(-p ,-q)$ définissent la même courbe $\gamma$ puisque son orientation n’est pas importante pour nous. On peut donc plus simplement penser au couple $(p,q)$ comme à une fraction réduite $p/q$ (la fraction $1/0=\infty$ étant autorisée). On note alors $K(p/q)$ la variété $K (\gamma )$ [2].
Représentations des 3-variétés par chirurgie sur un entrelacs
On définit de la même manière la chirurgie sur un entrelacs $\mathcal{L} \subset \mathbb{S}^3$. Cela revient à enlever des tores solides, voisinages des différentes composantes $L_i$ de $\mathcal{L}$, et à les recoller à nouveau le long des composantes de bord obtenues mais en changeant l’identification de façon que les courbes de chirurgie $\gamma_i$ bordent un disque méridien du tore solide. On note $L(\gamma_1,\dots,\gamma_n)$ la variété obtenue.
Un intérêt de la chirurgie de Dehn découle du résultat suivant dû à Lickorish [3] et Wallace [4] :
Pour toute $3$-variété compacte, orientable, connexe et fermée $V$ il existe un entrelacs $\mathcal{L}=L_1 \cup \dots \cup L_n$ de $\mathbb{S}^3$ et un choix de courbes $\gamma_1,\dots,\gamma_n$ tels que $V$ soit homéomorphe à la variété $L(\gamma_1,\dots,\gamma_n)$.
On dit alors que $L(\gamma_1,\dots,\gamma_n)$ est une présentation de $V$ par chirurgie de Dehn.

- Max Dehn (1878-1952)
Ce résultat permet donc de donner des descriptions purement combinatoires des $3$-variétés. De plus, on sait comment deux présentations par chirurgie de Dehn de la même variété sont reliées : elles différent par des mouvements de Kirby (voir Kirby [5], Fenn-Rourke [6] et Rolfsen [7]).
On peut suivre le même procédé pour obtenir des variétés fermées en partant de variétés quelconques à bord des tores à la place des extérieurs d’entrelacs : on parle alors de remplissage de Dehn.
Un exemple : les variétés obtenues par chirurgie de Dehn sur le nœud trivial
Considérons le cas où $k$ est le nœud trivial (et toujours $V = \mathbb{S}^3$.
Soit $p>0$. Si $q$ et $q'$ sont deux entiers congruents modulo $p$ alors les variétés $K(p/q)$ et $K(p/q' )$ sont homéomorphes.
Démonstration. Écrivons $q'=q+kp$ avec $k\in\mathbb{Z}$. Identifions $K$ avec
$$\{(w,e^{it})\in \mathbb{C} \times\mathbb{S}^1 \; | \; |w|\leq 1\}.$$
L’application définie par
$$(w,e^{it})\mapsto(we^{ikt},e^{it})$$
envoie la courbe $pm+q\ell $ sur la courbe $pm + q'\ell$. Il suffit alors d’appliquer le premier lemme de recollement.
C.Q.F.D.
$$ $$
On remarquera qu’il découle en particulier de cette proposition que le méridien n’est pas uniquement défini pour le nœud trivial.
Soit $K(p/q)$ la variété obtenue par chirurgie de Dehn sur le nœud trivial avec paramètre $\gamma=pm + q\ell$. On a alors :
- la variété $K(p/q)$ est homéomorphe à $\mathbb{S}^2 \times \mathbb{S}^1$ si $p=0$ (et donc $q=1$) ;
- la variété $K(p/q)$ est homéomorphe à $\mathbb{S}^3$ si $p=1$ ; $K(p/q)$ est homéomorphe à l’espace lenticulaire $L(p,q')$, où $0 < q' < p$, $q' \equiv q$ mod $p$, si $p>1$.
Démonstration. Les deux derniers points découlent immédiatement de la proposition. Pour le premier point il suffit d’observer que chaque disque méridien de $K$ est recollé le long de son bord à un disque méridien du tore solide ajouté, ce qui donne bien une $2$-sphère.
C.Q.F.D.
$$ $$
Puisque faire de la chirurgie de Dehn sur le nœud trivial revient à recoller ensemble deux tores solides, les variétés obtenues de cette façon coïncident avec les variétés admettant un scindement de Heegaard de genre $1$. Leurs groupes fondamentaux sont toujours monogènes.
Sphères d’homologie obtenues par chirurgie de Dehn sur un nœud
Revenons à l’étude d’un nœud quelconque $k$ dans $\mathbb{S}^3$. La première proposition ci-dessus permet de calculer l’homologie de la variété $K(p/q)$. Il découle en effet de la suite exacte longue de Mayer-Vietoris que $H_1(K(p/q))$ est le groupe abélien de présentation
$$\langle m ,\ell \; | \; \ell=0,\ p m+q\ell= 0 \rangle.$$
Ce groupe est trivial si $p=1$, monogène infini si $p=0$ et cyclique d’ordre $p$ dans les autres cas. Il en découle que la variété $K(p/q )$ est une sphère d’homologie entière si $p=1$ et une sphère d’homologie rationnelle pourvu que $p\neq 0$.
La variété dodécaédrique de Poincaré est une sphère d’homologie entière. On montre ici qu’on peut l’obtenir par chirurgie de Dehn de pente $-1$ sur le nœud de trèfle. Les sphères d’homologie ne peuvent toutefois pas toutes être obtenues par chirurgie de Dehn sur un nœud. [8] Une même sphère d’homologie peut par ailleurs être obtenue par chirurgie de Dehn sur des nœuds différents. [9]
[1] On prendra garde au fait que le couple $(m,\ell )$ n’est a priori pas uniquement déterminé par le nœud $k$, le choix du méridien dépend de l’identification $N(k) = \mathbb{D}^2 \times \mathbb{S}^1$. L’exemple du nœud trivial montre d’ailleurs qu’en général le méridien n’est pas uniquement déterminé. Toutefois, si $k$ n’est pas trivial les deux courbes $m$ et $\ell$ sont uniquement déterminées à isotopie près d’après un résultat (difficile) de Gordon et Luecke qui dit que si $k$ n’est pas le nœud trivial alors il admet une unique courbe de chirurgie $\gamma$, définie à isotopie près, telle que $K(\gamma)$ est la 3-sphère. Le lecteur intéressé pourra se reporter à : Cameron Gordon and John Luecke, Knots are determined by their complements. J. Amer. Math. Soc. 2 (1989), no. 2, 371–415.
[2] La courbe correspondant à la fraction $1/0=\infty$ est le méridien $m$. La variété $K(1/0)$ est donc la 3-sphère.
[3] Lickorish, W. B. R. A representation of orientable combinatorial 3-manifolds. Ann. of Math. (2) 76 1962 531–540.
[4] Wallace, Andrew H. Modifications and cobounding manifolds. Canad. J. Math. 12 1960 503–528.
[5] Rob Kirby, "A Calculus for Framed Links in S3". Inventiones Mathematicae, vol. 45 (1978), pp. 35–56
[6] R. P. Fenn and C. P. Rourke, "On Kirby’s calculus of links". Topology, vol. 18 (1979), pp. 1–15
[7] D. Rolfsen, Knots and links
[8] La somme connexe de deux sphères d’homologie est encore une sphère d’homologie : il s’agit là encore une fois d’une application de la suite de Mayer-Vietoris. On peut alors montrer qu’une sphère d’homologie entière qui est une somme connexe non triviale de sphères d’homologie ne peut pas être obtenue par chirurgie de Dehn sur un nœud. Pour les sphères d’homologie rationnelle ceci est bien plus facile à voir car il y a des variétés dont le premier groupe d’homologie est fini mais pas cyclique : c’est par exemple le cas de la variété dodécaédrique de Seifert-Weber.
[9] Tout nœud admet une chirurgie qui donne la $3$-sphère et, dans le cas du nœud trivial, même plusieurs chirurgies. Des exemples moins triviaux ont été construits par Lickorish, voir Lickorish W. B. R. Surgery on knots. Proceedings of the American Mathematical Society 1976 ;60:296-298.


