Un recollement du cube et une suspension d’un homéomorphisme du tore

On identifie les faces latérales du cube $[-1,1]^3$ par des translations, et les faces horizontales par un vissage d’un quart de tour, comme dans l’exemple 4 de Poincaré. L’espace $V$ obtenu est un cas particulier de suspension d’un automorphisme du tore. Il correspond à l’espace $K_{0,0,\pi/2}$ de la présentation générale des recollements du cube.

Le groupe fondamental de $V$ s’identifie naturellement au groupe de déplacements de $\mathbb{R}^3$ engendré par ces deux translations et ce vissage (voir là). Dans cet article nous allons vérifier que $V$ est bien une variété et calculer son groupe fondamental l’aide de la méthode de Poincaré.

Pour cela, on s’intéresse aux classes de sommets et d’arêtes de $V$. On dénombre trois classes de quatre arêtes, et une seule classe de sommets, représentés sur le figure ci-dessous.

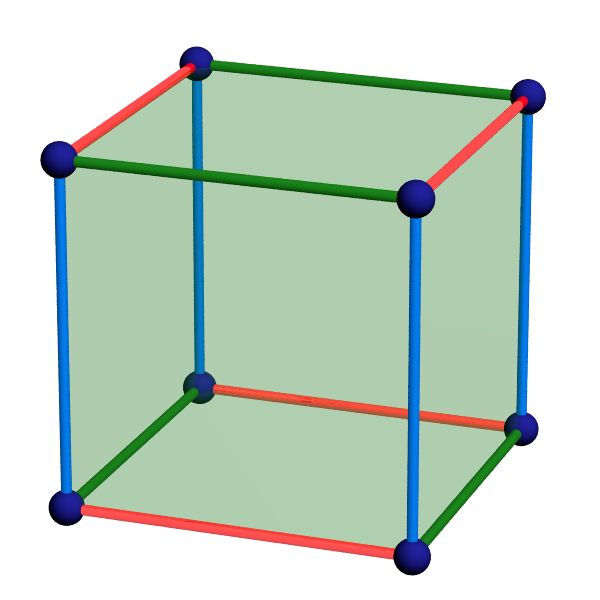
La caractéristique d’Euler de $V$ est donc $1-3+3-1=0$ et le critère de Poincaré implique que $V$ est une variété.

Passons maintenant au calcul du groupe fondamental. Avec les notations utilisées dans l’étude des recollements généraux d’une cube, les cycles d’arêtes sont les suivants :

$$\{Y^+ \cap X^+ , X^- \cap Y^+ , Y^- \cap X^- , X^+ \cap Y^- \} \quad \{ Y^+ \cap Z^+ , Z^-\cap X^+ , X^- \cap Z^- , Z^+\cap Y^- \}$$

$$ \{ Z^+ \cap X^+ , X^- \cap Z^+ , Z^- \cap Y^+, Y^- \cap Z^- \}.$$

À chacune correspond une relation liant les générateurs $I$, $J$, $K$ du groupe fondamental :

$$IJ I^{-1}J^{-1} =1,\quad K I K^{-1} J^{-1} =1,\quad I K J K^{-1} =1.$$

Autrement dit,

$$\pi_1(V)=\langle I,J,K\; | \; IJ=JI,\ KIK^{-1}=J,\ KJK^{-1}=I^{-1}\rangle.$$

Dans la description du groupe fondamental comme sous-groupe des déplacements engendré par deux translations et un vissage, les générateurs $I$ et $J$ correspondent aux translations et $K$ correspond au vissage (ce point de vue est détaillé dans cet article).