Le tore de dimension 3

On s’intéresse ici au premier exemple de recollement du cube décrit par Poincaré [1]. Cet exemple correspond à la variété $K_{0,0,0}$ décrite dans l’article général de présentation des recollements du cube. La variété $V$ considérée est obtenue en identifiant les faces opposées du cube $[-1,1]^3$ par des translations. L’espace obtenu est le tore $\mathbb{T}^3$, quotient de $\mathbb{R}^3$ par $\mathbb{Z}^3$. Cette action étant libre et propre et l’espace $\mathbb{R}^3$ étant simplement connexe, il découle de la définition du groupe fondamental que $\pi_1(V)$ est isomorphe à $\mathbb{Z}^3$.

Vérifions que $V$ est une variété et calculons son groupe fondamental à l’aide de la méthode de Poincaré.

Classes d’équivalences d’arêtes et de sommets dans l’exemple 1

Pour montrer que $V$ est une variété, on applique le critère présenté ici : $V$ est une variété si eu seulement si sa caractéristique d’Euler est nulle. Pour déterminer la caractéristique d’Euler, on s’intéresse aux classes d’arêtes et de sommets dans $V$.

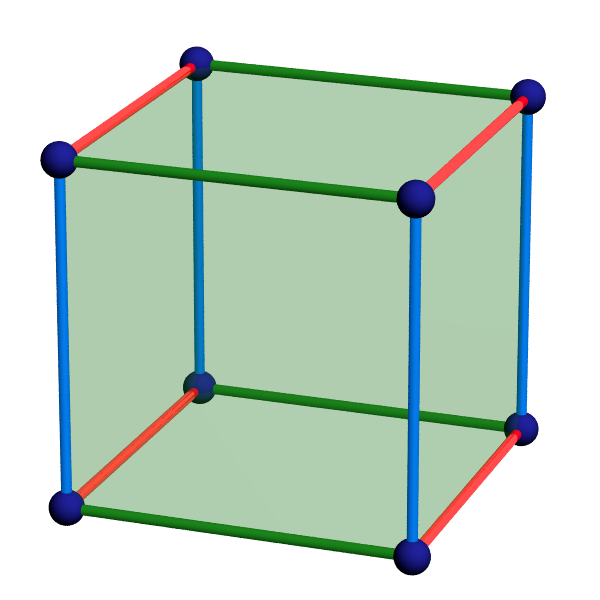
On dénombre trois classes d’arêtes formées chacune d’un quadruplet d’arêtes parallèles, comme sur la figure, et une seule classe de sommets.

La caractéristique d’Euler du quotient est donc

$$\chi(V) = 1-3+3-1=0,$$

et $V$ est bien une variété.

Présentation du groupe fondamental

Déterminons maintenant une présentation de son groupe fondamental en suivant la méthode générale de Poincaré ; les notations sont celles utilisées pour la description des recollements d’un cube. Les cycles d’arêtes sont les suivants :

$$( Y^+ \cap X^+ , X^- \cap Y^+ , Y^- \cap X^- , X^+ \cap Y^- ) \quad ( Y^+ \cap Z ^+ , Z^-\cap Y^+ , Y^- \cap Z^- , Z^+ \cap Y^-)$$

$$(Z^+\cap X^+,X^-\cap Z^+,Z^-\cap X^-,X^+\cap Z^-).$$

À chacun correspond une relation liant les générateurs $I$, $J$, $K$ du groupe fondamental :

$$I J I^{-1} J^{-1} =1,\quad K J K^{-1} J^{-1} =1,\quad I K I^{-1} K^{-1} =1.$$

Autrement dit,

$$\pi_1(V)=\langle I,J,K\;|\; IJ=JI,\;JK=KJ,\;IK=KI\rangle \simeq \mathbb{Z}^3.$$