Autour du groupe modulaire des surfaces

Soit $S$ une surface connexe et compacte à bord. La surface peut être non-orientable et le bord peut être vide.

Soient $f_0$ et $f_1$ deux élément du groupe $\mathrm{Homeo}(S)$ des homéomorphismes de $S$. Rappelons qu’une homotopie de $f_0$ à $f_1$ est une application continue $F: S\times \lbrack0,1 \rbrack \to S$ telle que $F_{|S\times \{0\}} = f_0$ et $F_{|S\times \{1\}} = f_1$. On dit que $F$ est une isotopie si, de plus, $F_{|S\times \{t\}}: S \to S$ est un homéomorphisme pour tout $t$. Si une homotopie (resp. une isotopie) entre $f_0$ et $f_1$ existe, on dit que $f_0$ et $f_1$ sont homotopes (resp. isotopes). Si $S$ est une surface à bord et si $f_0$ et $f_1$ valent l’identité sur le bord, on dira que $f_0$ et $f_1$ sont homotopes (resp. isotopes) relativement au bord s’il existe une homotopie (resp. isotopie) $F$ de $f_0$ à $f_1$ telle que pour tout $t$, $F_{|S\times \{t\}}$ vaut l’identité sur le bord de $S$.

Exemple. Toute translation du tore $\mathbb{T}^2=\mathbb R^2 / \mathbb Z^2$ est isotope à l’identité. En effet, la translation $T_v: x \mapsto x+v$ de vecteur $v$ est reliée à l’application identité du tore (translation de vecteur nul) par l’isotopie $F(t)=T_{tv}$, où $T_{tv}$ est la translation de vecteur $tv$, pour tout $t \in \lbrack 0, 1 \rbrack.$

Notons que la définition de $\mathrm{Mod}^{+}(S)$ ne dépend pas du choix d’orientation de $S$.

Dans le cas des surfaces à bord on s’intéressera également au groupe $\mathrm{Mod}(S, \partial S)$ formé par les classes d’isotopie d’homéomorphismes de $S$ égaux à l’identité sur le bord $\partial S$.

Les notions d’homotopie et d’isotopie sont a priori différentes, et il est souvent plus facile de construire une homotopie qu’une isotopie. Heureusement, le théorème suivant affirme que ces deux notions sont essentiellement les mêmes pour les surfaces :

Groupe modulaire du cylindre et twist de Dehn

Soit $C = \mathbb{S}^1 \times \lbrack 0, 1 \rbrack$ le cylindre. Calculons le groupe modulaire $\mathrm{Mod}(C, \partial C)$.

Démonstration. Considérons $f$ une classe d’isotopie d’homéomorphismes de $C$ qui valent l’identité sur le bord. Relevons $f$ au revêtement universel $\tilde C = \mathbb R \times \lbrack 0, 1 \rbrack$. Plus précisément, considérons l’unique relèvement $\bar{f}$ de $f$ tel que $\bar{f}(0,0)=(0,0)$. Comme l’application $\bar{f}$ relève l’identité sur le bord de $\tilde C$, elle coïncide avec l’identité sur la composante de bord $\mathbb R \times \{0 \}$ et avec une translation entière de longueur $n$ sur la composante de bord $\mathbb R \times \{ 1 \}$. Associons à $f$ le nombre entier $n$. On vérifie aisément que cette application est un morphisme de groupes entre le groupe modulaire $\mathrm{Mod}(C, \partial C)$ de $C$ et $\mathbb Z$. Montrons que c’est un isomorphisme.

Pour démontrer la surjectivité, choisissons $n \in \mathbb Z$ et notons que l’application linéaire $ \left (\begin{array}{ll} 1 & n \\ 0 & 1 \end{array} \right )$ préserve $\tilde C= \mathbb R \times \lbrack 0, 1 \rbrack$ vu comme sous-ensemble de $\mathbb R^2$. Par ailleurs, cette application linéaire passe au quotient en un homéomorphisme de $C$. Comme le relevé est l’application linéaire initiale et que celle-ci agit sur la composante de bord $\mathbb R \times \{1 \}$ de $\tilde C$ par une translation de longueur $n$, on vient de trouver une pré-image de $n \in \mathbb Z$ dans le groupe modulaire de $C$.

Passons à la preuve de l’injectivité. Considérons à cette fin un élément du groupe modulaire qui est d’image nulle dans $\mathbb Z$ par le morphisme précédent. Il se relève donc en un homéomorphisme $\bar{f}$ de $\tilde{C}=\mathbb R \times \lbrack 0, 1 \rbrack$ qui vaut l’identité sur les deux composantes du bord. L’application $F:(t,x) \mapsto t \bar{f}(x) +(1-t)x$ descend alors en une homotopie entre $f$ et l’identité, qui vaut l’identité en restriction à $\partial C \times \{t\}$. D’après le théorème de Baer, $f$ est donc isotope à l’identité, ce qui conclut la preuve.

C.Q.F.D.

Le groupe modulaire du cylindre est donc infini cyclique, engendré par l’homéomorphisme défini par l’application linéaire

$$ \left (\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array} \right ).$$

Il y a en fait — modulo isotopie — deux twists de Dehn possibles. Si on a fixé une orientation de $C$, on peut distinguer le twist de Dehn à droite du twist de Dehn à gauche. Cette distinction sera importante dans l’article La formule de Picard-Lefschetz.

Twist de Dehn à droite

Groupe modulaire du tore

Comme pour le cylindre, nous allons voir que tout homéomorphisme du tore $\mathbb{T}^2 = \mathbb{R}^2/\mathbb{Z}$ est isotope à un automorphisme linéaire. En revanche, le groupe des automorphismes linéaires du tore est beaucoup plus riche que celui du cylindre. Les suspensions d’automorphismes linéaires du tore constituent une famille importante de $3$-variétés classifiées par leur groupe fondamental, introduites par Poincaré dès la Note de 1892.

Pour "linéariser" les automorphismes du tore, on commence par regarder leur action sur le premier groupe d’homologie. L’action canonique du groupe des homéomorphismes de $\mathbb{T}^2$ sur $H_1\left(\mathbb{T}^2,\mathbb{Z}\right)\simeq \mathbb{Z}^2$ en homologie passe en effet au quotient en une action du groupe modulaire, et on obtient ainsi un morphisme de groupes

$$i: \mathrm{Mod}(\mathbb{T}^2) \to \mathrm{GL}(2,\mathbb{Z}).$$

Le théorème suivant, dû à Poincaré, affirme que ce morphisme est en fait un isomorphisme :

Démonstration.
Pour montrer la surjectivité, il suffit d’observer que l’action linéaire de toute matrice $A \in \mathrm{GL}(2, \mathbb Z)$ passe au quotient en un homéomorphisme $\bar{A}$ du tore $\mathbb T^2=\mathbb R^2 / \mathbb Z^2$. De plus, l’action de $\bar{A}$ sur le $H_1(\mathbb T^2, \mathbb Z)$ se lit dans la base canonique comme l’action linéaire de $A$ sur $\mathbb Z^2$. La restriction de $i$ aux homéomorphismes linéaires est donc surjective. En particulier, $i$ sera surjectif.

Passons maintenant à la preuve de l’injectivité. Considérons $f$ un élément du groupe modulaire qui agit trivialement sur $H_1(\mathbb T^2, \mathbb Z)$. Soit $\bar{f}$ un relèvement de $f$ à $\mathbb{R}^2$. Comme $f$ agit trivialement sur $H_1(\mathbb T^2, \mathbb Z) = \mathbb{Z}^2$, on déduit que $\bar{f}$ commute avec l’action de $\mathbb{Z}^2$ par translations. L’application $F:(t,x) \mapsto t \bar{f}(x) +(1-t)x$ descend alors en une homotopie entre $f$ et l’identité. Cette homotopie n’a a priori aucune raison d’être une isotopie, mais le théorème de Baer permet alors de conclure que $f$ est isotope à l’identité.

C.Q.F.D

Remarquons que la preuve précédente s’adapte facilement au cas de la surface non compacte $S_{1,1}$ qui est le tore épointé. On observe que l’on a toujours $H_1(S_{1,1}, \mathbb Z) \simeq \mathbb Z^2$ et dans ce cas le morphisme $i : \mathrm{Mod}(S_{1,1}) \to \mathrm{Aut}(\mathbb Z^2)$ donné par l’action en homologie est encore un isomorphisme :

La vidéo suivante propose un cours filmé traitant des résultats ci-dessus. La preuve donnée dans la vidéo est un peu différente : pour éviter d’avoir recours au théorème de Baer, on y utilise l’astuce d’Alexander.

Groupe modulaire des surfaces de genre supérieur

Passons à présent au cas des surfaces compactes orientables $S$ de genre $g \geq 2$. Comme pour le tore, nous commençons par étudier l’action du sous-groupe $\mathrm{Mod}_+(S)$ d’indice $2$ de $\mathrm{Mod}(S)$ sur $H_1(S,\mathbb Z) \simeq \mathbb Z^{2g}$. Cette action préserve la forme d’intersection $\wedge$. D’après le théorème de dualité de Poincaré, cette forme d’intersection est une forme bilinéaire anti-symétrique non dégénérée.

Dans le cas précédent du tore $T^2$, cette forme bilinéaire coïncide avec le déterminant. Dans le cas des surfaces de genre $g \geq 2$, Poincaré démontre le théorème suivant :

Rappelons que $\mathrm{Sp}(2g, \mathbb Z)$ désigne le groupe des matrices symplectiques à coefficients entiers, de taille $(2g) \times (2g)$.

Démonstration.
Dans le Cinquième complément Poincaré démontre ce théorème dans le but de montrer ensuite qu’un élément non nul dans $H_1(S, \mathbb Z)$ peut être représenté par une courbe simple fermée si et seulement si cet élément est primitif (voir nos commentaires). De nos jours on commence en général par montrer ce dernier résultat directement, à l’aide d’un analogue de l’algorithme d’Euclide pour les courbes fermées simples [2].

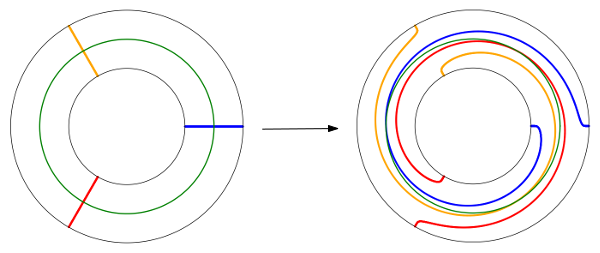
Fixons une courbe fermée simple $a$ sur $S$. Soit $C$ un voisinage de $a$ homéomorphe à un cylindre. On peut alors prolonger un générateur de $\mathrm{Mod}(C,\partial C)$ en un homéomorphisme $T_a$ de $S$, appelé twist de Dehn le long de $a$.

On montre ensuite que l’action du twist de Dehn $T_a$ autour d’une courbe fermée simple qui représente l’élément $a \in H_1(S, \mathbb Z)$ est une transvection symplectique

$$T_a : b \to b+(a \wedge b)a.$$

Les vidéos suivantes montrent un twist de Dehn sur un tore et sur une surface de genre $3$. La courbe $a$ est représentée en rouge et une courbe $b$ est représentée en bleue. Dans le cas du tore, on observe que le twist de Dehn est homotope à un automorphisme linéaire donné par une matrice unipotente.

On peut maintenant conclure la démonstration du théorème grâce au lemme suivant :

Besoin d’une démonstration ?

Commençons par énoncer un fait élémentaire crucial.

Notons $G$ le groupe engendré par les transvections symplectiques. Nous allons utiliser le fait ci-dessus pour démontrer le lemme suivant.

Démonstration. Soient $(a,b)$ et $(u,v)$ deux couples de vecteurs primitifs tels que

$$a \wedge b = u \wedge v =1.$$

Commençons par montrer qu’il existe un élément de $G$ qui envoie $a$ sur $u$.

On écrit $u=na + m b + u'$ avec $u'$ orthogonal au plan engendré par les vecteurs $a$ et $b$. Puisque

$$a \wedge (a+b ) = 1 \mbox{ et } (a+b) \wedge b = 1,$$

le fait ci-dessus implique que le groupe $G$ permet de réaliser l’algorithme d’Euclide sur le vecteur $na+mb$. Il existe donc un élément de $G$ qui envoie $u$ sur $\mathrm{pgcd}(n,m) a + u'$.

On est donc ramené à supposer que $u = na + m u'$ avec $u'$ primitif, orthogonal au plan engendré par $a$ et $b$ et $n$ et $m$ premiers entre eux. Il existe alors un vecteur $v'$ primitif orthogonal au plan engendré par $a$ et $b$ et tel que $u' \wedge v' = 1$. Et puisque

$$a \wedge (b + v') = 1 \mbox{ et } u' \wedge (b+ v') =1,$$

le fait ci-dessus implique encore que le groupe $G$ permet de réaliser l’algorithme d’Euclide sur le vecteur $na+mu'$. Il existe donc un élément de $G$ qui envoie $u$ sur $a$.

On est donc ramené à supposer que $u=a$ et donc $v=b + v'$ avec $a \wedge v'=0$. On peut de plus supposer que $b \wedge v' =0$. On a alors

$$(a+b) \wedge b \mbox{ et } (a+b) \wedge v = 1$$

et le fait ci-dessus implique alors que la composée de la transvection symplectique $T_{a}$ par $T_{v'-a}^{-1}$ envoie le vecteur $b$ sur $v'$ sans bouger $a$. Ce qui conclut la démonstration du lemme.

C.Q.F.D.

$$ $$

On peut maintenant montrer que $G=\mathrm{Sp}(2g, \mathbb Z)$ par récurrence sur $g$. Soient $u$ et $v$ deux vecteurs primitifs de $\mathbb{Z}^{2g}$ tels que $u \wedge v=1$. Ces vecteurs sont nécessairement linéairement indépendants et engendrent un plan $W$ en restriction auquel la forme symplectique est non-dégénérée. Étant donnée une transformation $S \in \mathrm{Sp}(2g, \mathbb Z)$, les vecteurs $Su$ et $Sv$ sont encore primitifs et on a $Su \wedge Sv =1$. Il découle alors du lemme précédent qu’il existe une transformation $T \in G$, telle que

$$TSu = u \mbox{ et } TSv =v .$$

On a donc

$$TS_{|W} = \mathrm{Id}_W$$

et, puisque

$$TS_{| W^{\perp}} \in \mathrm{Sp} ( W^{\perp} ) \cong \mathrm{Sp}(2(g-1), \mathbb Z)$$

le résultat pour $\mathrm{Sp}(2g, \mathbb Z)$ s’en déduit.

C.Q.F.D.

$$ $$

C.Q.F.D.

Remarquons que le morphisme précédent $i$ n’est pas injectif. En effet, soit $a$ une courbe fermée simple sur $S$ qui borde une surface sans border de disque. Elle représente par conséquent un élément trivial du $H_1(S, \mathbb Z)$. Alors $T_a$ agit trivialement en homologie, donc appartient au noyau du morphisme $i$. Par ailleurs, cet élément n’est pas trivial dans le groupe modulaire car, par exemple, il agit de manière non triviale sur le groupe fondamental de $S$.

Pour être plus précis, fixons un point base $x$ sur $S$. Le groupe modulaire de $S$ relativement à $x$ (c’est-à-dire le groupe des homéomorphismes de $S$ fixant $x$ modulo isotopie fixant $x$ à chaque instant $t$) agit par automorphismes sur $\pi_1(S,x)$. Par ailleurs, tout homéomorphisme de $S$ peut être isotopé à un homéomorphisme fixant $x$. Par contre, deux homéomorphismes fixant $x$ qui sont isotopes ne le sont pas nécessairement relativement à $x$. Leur action sur le groupe fondamental diffère par un automorphisme intérieur, c’est-à-dire un automorphisme de la forme $g\mapsto hgh^{-1}$ pour un certain $h$. On en déduit un morphisme

$$j: \mathrm{Mod}(S,x) \to \mathrm{Aut}(\pi_1(S)) / \mathrm{Int}(\pi_1(S))~,$$

où $\mathrm{Int}(\pi_1(S))$ désigne le sous-groupe normal des automorphismes intérieurs. Le quotient $ \mathrm{Aut}(\pi_1(S)) / \mathrm{Int}(\pi_1(S))$ est généralement appelé groupe des automorphismes extérieurs de $\pi_1(S)$ et se note $\mathrm{Out}(\pi_1(S))$. On a le théorème suivant :

Autrement dit, on comprend tout le groupe modulaire en regardant son action sur le groupe fondamental. Ce résultat aurait sans doute ravi Poincaré !