
|
> Introduction à l’Analysis situs par les surfaces > Revêtements ramifiés entre surfaces Revêtements ramifiés entre surfaces |
Historiquement, la notion de revêtement ramifié est indissociable de celle de revêtement : les deux sont apparues dans l’étude des surfaces de Riemann. En effet, la plupart des applications holomorphes entre surfaces de Riemann sont des revêtements en dehors de "points de ramifications" isolés, où l’application $f$ considérée s’écrit localement
$$f:z \mapsto z^k$$
pour un entier $k > 1$ et une coordonnée locale complexe $z$. Cela conduit à la définition suivante :
Soit $X$ et $Y$ deux variétés topologiques orientées de dimension $2$ et $f : X → Y$ une application continue. On dit que $f$ est un revêtement ramifié si pour tout $y \in Y$, il existe
- un voisinage $U$ de $y$ et un homéomorphisme $\Psi: U \to V \subset \mathbb{C}$,
- une application $k$ de $F= f^{-1}(y)$ dans $\to \mathbb{N}\backslash \{0\}$,
- un difféomorphisme $\Phi$ de $f^{-1}(U)$ dans $V \times F$,
tels que pour tout $x\in F$, en restriction à $V \times \{x\}$, on a
$$\Psi \circ f \circ \Phi^{-1}: z \mapsto z^{k(x)}~.$$
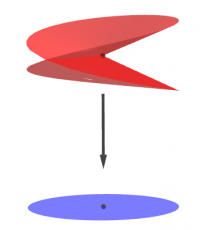
- La projection verticale de la surface rouge sur le disque bleu est un revêtement de degré $2$ ramifié au dessus du centre du disque.
On peut montrer que l’entier $k(x)$ ne dépend pas du choix des coordonnées locales $(U,\Phi)$ et $(V,\Psi)$. On l’appelle l’indice de ramification de $f$ en $x$. Si $k(x) = 1$, alors $f$ est un difféomorphisme local au voisinage de $x$. Si $k(x)>1$, on dit que $x$ est un point de ramification de $f$. On appelle lieu de ramification de $f$ l’image de l’ensemble des points de ramification. La forme locale d’un revêtement ramifié montre que le lieu de ramification de $f$ est un sous-ensemble discret de $Y$. On obtient finalement :
Soit $f:X \to Y$ un revêtement ramifié. Notons $Y_{reg}$ le complémentaire dans $Y$ du lieu de ramification et $X_{reg} = f^{-1}(Y_{reg})$. Alors
$$f: X_{reg} \to Y_{reg}$$
est un revêtement.
Le degré d’un revêtement ramifié de $X$ dans $Y$ désigne simplement le degré du revêtement induit de $X_{reg}$ dans $Y_{reg}$.
La proposition suivante est la motivation principale pour l’étude des revêtements
ramifiés :
Toute application holomorphe propre et non constante entre deux surfaces de Riemann est un revêtement ramifié de degré fini. En particulier, toute application holomorphe entre deux surfaces de Riemann compactes est un revêtement ramifié de degré fini.
Démonstration. Il s’agit d’un résultat classique d’analyse complexe. En coordonnées locales, toute application holomorphe non constante s’écrit
$$f : z \mapsto z^k g(z)~,$$
où $g(0) \neq 0$.
Comme on peut définir une fonction "racine $k$-ième" au voisinage de tout point de $\mathbb{C}^*$, on peut écrire localement
$$g(z) = h(z)^k~.$$
On pose alors $\phi(z) = z h(z)$. La dérivée de $\phi$ en $0$ est non nulle, donc $\phi$ est un difféomorphisme local au voisinage de $0$ et on a
$$f\circ \phi^{-1}(z) = z^k~.$$
Enfin, si $f$ est propre, la fibre au dessus d’un point $z'$ est finie et on peut donc trouver un voisinage $U$ de $z'$ et des coordonnées locales sur $f^{-1}(U)$ telles que $f$ s’écrit en coordonnées locales comme une puissance de $z$ sur chaque composante connexe de $f^{-1}(U)$.
C.Q.F.D.
Quelques exemples
- L’application holomorphe $f: \mathbb{C}^* \to \mathbb{C}$ définie par
$$f(z) = z + z^{-1}$$
est un revêtement ramifié de degré 2. Ses deux points de ramifications sont $1$ et $−1$.
- L’application
$$f: (\mathbb{R}/2\pi \mathbb{Z})^2 \to \mathbb{R}^3$$
définie par
$$f(\theta, \phi) = (\cos(\theta), \cos(\phi), \cos(\theta+\phi))$$
a pour image la cubique $\mathcal{C}$ d’équation
$$X^2+Y^2+Z^2-2XYZ = 1~,$$
qui est homéomorphe à une sphère. L’application induite
de $(\mathbb{R}/2 \pi \mathbb{Z})^2$ dans $\mathcal{C}$ est un revêtement double ramifié aux quatre points $(m\pi, n\pi)$ avec $m,n \in \mathbb{Z} / 2\mathbb{Z}$.
- La fonction $\mathfrak{p}$ de Weierstrass est également un revêtement du tore sur la sphère ramifié en $4$ points.
Formule de Riemann—Hurwitz
Soit $X$ et $Y$ deux surfaces compactes connexes et $f: X \to Y$ un revêtement ramifié. La formule de Riemann-Hurwitz exprime la caractéristique d’Euler de $X$ en fonction de la caractéristique d’Euler de $Y$, du degré du revêtement et du nombre de points de branchements (comptés avec multiplicité).
On a l’égalité suivante :
$$\chi(X) = \deg(f) \chi(Y) - \sum_{x\in X} (k_x-1)~.$$
Comme la caractéristique d’Euler classifie topologiquement les surfaces fermées orientables, la formule de Riemann—Hurwitz caractérise donc complètement la topologie d’un revêtement ramifié d’une surface orientable. C’est un résultat fort. En effet, il n’est pas simple de visualiser la topologie d’un revêtement ramifié à partir de la donnée de son degré et du nombre de points de branchements, ni même de se convaincre que ces données déterminent totalement la topologie du revêtement.
Démonstration de la formule de Riemann—Hurwitz.
Soit $C \subset X$ l’ensemble des points de ramification de $f$. Considérons une triangulation de $Y$ dans laquelle les points de $f(C)$ sont des sommets. On note $S$, $A$ et $F$ le nombre de sommets, arêtes et faces de cette triangulation.
Cette triangulation se "tire en arrière" par $f$ et fournit une triangulation de $X$, qui possède $\deg(f) A$ arêtes et $\deg(f) F$ faces. On serait tenté de dire qu’elle possède aussi $\deg(f) S$ sommets (ce serait le cas si $f$ était un vrai revêtement) mais on compterait alors $k_x$ fois un point $x$ de $C$, ce qui est $k_x-1$ fois de trop. La triangulation de $X$ possède donc $ \deg(f) S - \sum_{x\in C} k_x-1$ sommets. On a alors
$$ \begin{array}{cl} \chi (X) & = \deg ( f ) F - \deg ( f ) A + \deg (f) S - \sum_{x\in C} k_x -1 \\ & = \deg ( f ) \chi ( Y ) - \sum_{x \in C} k_x -1 . \end{array} $$
C.Q.F.D.
Construction de revêtements ramifiés
Nous venons de voir que la topologie d’un revêtement ramifié au dessus d’une surface $Y$ est caractérisée par le degré du revêtement et le nombre de points de branchement comptés avec multiplicité. On peut se demander si cette donnée caractérise aussi le revêtement.
Soit $f:X \to Y$ et $f':X' \to Y$ deux revêtements ramifiés. On dit que ces deux revêtements sont isomorphes s’il existe un homéomorphisme $\Phi: X \to X'$ tel que
$$f' \circ \Phi = f~.$$
Nous aborderons pas le problème de classifier les revêtements ramifiés à isomorphisme près. Nous nous contentons ici du cas des revêtements doubles, qui admet une réponse particulièrement claire.
Soit $S$ une surface compacte orientée et $p_1, \ldots , p_n$ des points distincts de $S$. Alors il existe un revêtement double de $S$ ramifié au-dessus des points $p_1, \ldots , p_n$ si et seulement si $n$ est pair. L’ensemble des classes d’isomorphisme de revêtements ramifiés en $p_1, \ldots , p_n$ est un espace affine sur $H_1(S, \mathbb{Z}/2\mathbb{Z})$. En particulier, cette ensemble est de cardinal $4^g$, où $g$ désigne le genre de $S$.
Démonstration. Supposons qu’un tel revêtement $f:X \to S$ existe. Notons $S'$ la surface $S$ privée des points $p_1, \ldots , p_n$. Choisissons un point base $p$ de $S'$. Soit
$$\rho: \pi_1(S') \to \mathfrak{S}_2 \simeq \mathbb{Z}/ 2 \mathbb{Z}$$
le morphisme de monodromie du revêtement induit par $f$ au dessus de $S'$.
Le groupe fondamental de $S'$ admet une présentation de la forme
$$\left \langle \alpha_1, \beta_1, \ldots \alpha_g, \beta_g, \gamma_1, \ldots \gamma_n \mid \prod_{i=1}^g [\alpha_i, \beta_i] \cdot \prod_{j=1}^n \gamma_j = 1 \right \rangle~,$$
où $\gamma_i$ est la classe d’homotopie d’un lacet entourant $p_i$. Comme $\rho$ est à valeurs dans un groupe abélien, on a
$$\sum_{j=1}^n \rho(\gamma_j) = - \sum_{i=1}^g \rho([\alpha_i, \beta_i]) = 0~.$$
Or, comme $f: X \to S$ ramifie en $p_i$, on a $\rho(\gamma_i) \neq 0$ pour tout $i$. On en déduit que $n$ doit être pair.
Réciproquement, si $n$ est pair, on peut construire un morphisme $\rho$ de $\pi_1(S')$ dans $\mathbb{Z}/ 2 \mathbb{Z}$ tel que l’image de $\gamma_i$ est non nulle pour tout $i$. Il existe alors un unique revêtement double au dessus de $S'$ de monodromie $\rho$. Au dessus d’un anneau entourant $p_i$, ce revêtement double est isomorphe au revêtement double
$$ \begin{array}{rcl} \mathbb{C}^* & \to & \mathbb{C}^*\\ z & \mapsto & z^2 \end{array} $$
(puisque sa monodromie est non triviale). Ce revêtement se prolonge donc en un revêtement double sur $S$ ramifié en $p_1, \ldots p_n$.
Les revêtements doubles de $S$ ramifiés en $p_1, \ldots p_n$ sont donc paramétrés par les morphismes de $\pi_1(S')$ dans $\mathbb{Z}/ 2 \mathbb{Z}$ tels que l’image de chaque $\gamma_i$ est non nulle. La différence entre deux tels morphisme est un morphisme qui s’annule sur les $\gamma_i$ et induit donc un élément de
$$H^1(S,\mathbb{Z}/2\mathbb{Z}) = \mathrm{Hom}(\pi_1(S), \mathbb{Z}/2\mathbb{Z})~.$$
C.Q.F.D.
Exemple. Comme le groupe fondamental de la sphère est trivial, il existe un unique revêtement de la sphère ramifié en $2n$ points. D’après la formule de Riemann-Hurwitz, c’est une surface de genre $n-1$. En particulier, les deux exemples donnés précédemment de revêtements du tore sur la sphère ramifiés en 4 points sont topologiquement isomorphes.

