Un invariant topologique : la caractéristique d’Euler-Poincaré d’une surface fermée

Cet article illustre dans le cas des surfaces un invariant topologique fondamental en topologie algébrique : la caractéristique d’Euler—Poincaré. La caractéristique d’Euler—Poincaré fait l’objet d’une présentation plus approfondie dans le cours sur l’homologie.

Qu’est-ce qu’un "invariant topologique" ?

Si vous êtes arrivés ici en suivant l’Introduction à l’Analysis Situs par les surfaces, vous connaissez maintenant un grand nombre de surfaces : la sphère, le tore, les surfaces fermées de genre $g\geq 2$ (obtenues comme sommes connexes de tores, voir ici), la bouteille de Klein... Mais comment être sûr que ces surfaces sont toutes différentes ? Qu’on ne peut pas, par une contorsion compliquée, transformer l’une en l’autre ? C’est à cela que sert un invariant topologique.

Un invariant topologique est un objet associé à une variété (le plus souvent un nombre ou un groupe), qui est invariant par homéomorphisme (c’est-à-dire que la valeur de cet invariant est la même pour deux variétés homéomorphes), et qu’on peut espérer calculer explicitement (au moins dans certains cas). Si ce calcul donne des résultats différents sur deux variétés $V_1$ et $V_2$, c’est donc que ces variétés ne sont pas homéomorphes ! On peut dire que le but de toute la topologie algébrique est de construire des invariants topologiques.

Bien sûr, il se pourrait que le calcul d’un invariant topologique donne la même chose sur deux variétés qui ne sont pas homéomorphes. La dimension d’une variété, par exemple, est un invariant topologique, mais il ne risque pas de nous aider à distinguer les surfaces !

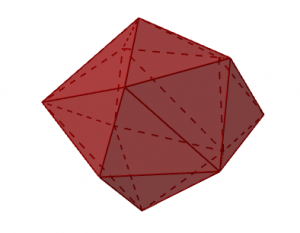
Un polyèdre sphérique à $12$ sommets, $30$ arêtes et $20$ faces.

Dans cet article, nous présentons un invariant topologique plus fin, qui permet de distinguer les surfaces orientables.

La formule d’Euler pour les polyèdres sphériques

Considérons un polyèdre homéomorphe à la sphère de dimension $2$ (c’est par exemple le cas pour tout polyèdre convexe). Soit $S$, $A$ et $F$ le nombre de sommets, faces et arêtes de ce polyèdre. Un célèbre théorème d’Euler affirme alors que

$$S-A+F = 2~,$$

et ce quelque soit le polyèdre.

On peut tester cette conjecture sur le polyèdre ci-contre, qui a $12$ sommets, $30$ arêtes et $20$ faces (il s’agit d’un icosaèdre).

Caractéristique d’Euler d’une surface

L’image ci-dessous montre qu’on peut construire des polyèdres homéomorphes à d’autres surfaces que la sphère (au tore, en l’occurrence). Plus généralement, toutes les surfaces admettent des décompositions polyédrales, c’est-à-dire des décompositions en sommets, arêtes est faces, où les arêtes peuvent être courbes et où les faces sont homéomorphes à des disques bordés par un nombre fini d’arêtes. (N’oublions pas que nous nous intéressons aux propriétés des surfaces qui sont invariantes par déformation). Le théorème d’Euler se généralise alors de la façon suivante :

Indications pour la preuve.

La preuve repose essentiellement sur les quatre remarques suivantes, dont les détails des preuves sont laissés au lecteur.

1. Si l’on subdivise une décomposition polyédrale d’une surface compacte (éventuellement à bord), cela ne change pas le nombre $S-A+F$. Pour le démontrer, on pourra noter qu’il suffit de considérer le cas où on coupe une face en deux par un segment qui joint deux points du bord de cette face.
2. Si l’on part d’une surface compacte (éventuellement à bord) munie d’une décomposition polyhédrale, et que l’on découpe cette surface le long d’une courbe fermée constituée d’une suite d’arrêtes et de sommets de la décomposition polyédrale, cela ne change pas le nombre $S-A+F$. En effet, la courbe de découpage est un polygone fermée constitué de $n$ arrêtes et $n$ sommets. Le découpage augmente donc les entiers $A$ et $S$ de $n$ unités chacun.
3. Si l’on part d’une surface compacte à bord munie d’une décomposition polyédrale, et que l’on découpe cette surface le long d’un arc, allant du bord au bord, constitué d’une suite d’arrêtes et de sommets de la décomposition polyédrale, cela augmente le nombre $S-A+F$ d’une unité. La preuve est la même que pour le point précédent ; la seul différence étant que l’arc le long duquel on découpe est constitué de $n$ arrêtes et $n+1$ sommets.
4. Pour une décomposition polyhédrale finie d’un disque topologique, le nombre $S-A+F$ vaut toujours $1$. Pour le montrer, on part d’une face de la décomposition, puis on recolle les faces une après l’autre.

Considérons maintenant une surface compacte $\Sigma$, et une décomposition polyédrale $P$ de $\Sigma$. Partant de $\Sigma$, on arrive à une famille finie de disques fermés (à homéomorphismes) par une suite de découpage de le long de courbes fermées et d’arcs allant du bord au bord. Le nombre de disque obtenus à la fin ne dépend que de $\Sigma$ et des classes d’homotopies des courbes fermées et des arcs de découpages. Quitte à subdiviser $P$ (ce qui ne change pas l’entier $S-A+F$ d’après le point 1 ci-dessus), ceci permet de supposer que les courbes et arcs de découpages sont constitués d’arêtes et de sommets de $P$. En utilisant les points 2, 3 et 4 ci-dessus, on en déduit que l’entier $S-A+F$ ne dépend pas de $P$.

Une preuve légèrement différente découlera de la classification des surfaces triangulées par réduction à une forme canonique.

Dans le paragraphe de l’Analysis Situs, Poincaré généralise la proposition ci-dessus en dimension quelconque, et en donne une preuve conceptuelle, basée sur le concept d’homologie. Une formulation moderne de cette preuve — pour les lecteurs maitrisant le concept d’homologie — se trouve ici.

Un polyèdre homéomorphe au tore, avec 21 sommets, 63 arêtes et 42 faces.

D’après le théorème d’Euler, la caractéristique d’Euler de la sphère est donc égale à $2$. De même, on peut vérifier que la décomposition polyédrale du tore ci-dessus possède $21$ sommets, $63$ arêtes et $42$ faces. La caractéristique d’Euler du tore est donc égale à

$$21 - 63 +42 = 0~.$$

Caractéristique d’Euler d’une somme connexe.

La caractéristique d’Euler de la somme connexe de deux surfaces $\Sigma_1$ et $\Sigma_2$ se calcule grâce à la formule suivante :

$$\chi\left(\Sigma_1 \sharp \Sigma_2\right) = \chi(\Sigma_1) + \chi(\Sigma_2) -2~.$$

Démonstration.

Choisissons des décompositions polyédrales de $\Sigma_1$ et $\Sigma_2$. Quitte à les subdiviser, on peut supposer que toutes les faces sont des triangles. Notons $S_i$, $A_i$ et $F_i$ le nombre de sommets, arêtes et faces de la décomposition polyédrale de $\Sigma_i$. La réunion de $\Sigma_1$ et $\Sigma_2$ admet donc une décomposition polyédrale avec $S_1+S_2$ sommets, $A_1+A_2$ arêtes et $F_1+ F_2$ faces.

Pour réaliser la somme connexe de $\Sigma_1$ et $\Sigma_2$, retirons deux triangles $T_1$ et $T_2$ dans $\Sigma_1$ et $\Sigma_2$ respectivement, puis collons les côtés de $T_1$ avec ceux de $T_2$. Cette opération nous a fait perdre $2$ faces (les triangles $T_1$ et $T_2$), trois arêtes (puisqu’on a fusionné deux par deux les côtés de $T_1$ et ceux de $T_2$) et trois sommets (pour la même raison). On a donc :

$$ \begin{eqnarray*} \chi\left( \Sigma_1 \sharp \Sigma_2\right) &=& (S_1 + S_2 -3) - (A_1 +A_2 -3) + (F_1+F_2-2)\\ &=&(S_1-A_1+F_1) +(S_2-A_2+F_2) -3 +3 -2 \\ &=& \chi(\Sigma_1) + \chi(\Sigma_2) -2~. \end{eqnarray*} $$

Puisque la caractéristique d’Euler du tore $\mathbb{T}^2$ est nulle, on a donc

$$\chi \left(\Sigma \sharp \mathbb{T}^2 \right) = \chi(\Sigma)-2$$

pour toute surface $\Sigma$. On en déduit aisément la caractéristique d’Euler de la somme connexe de $g$ tores :

Soient $g_1$ et $g_2$ deux entiers distincts. Puisque $\chi(\Sigma_{g_1}) \neq \chi(\Sigma_{g_2})$, on peut donc conclure que les surfaces de genre $g_1$ et $g_2$ ne sont pas homéomorphes.

Une application : triangulations minimales d’une surface compacte

Soit $\Sigma$ une surface fermée de genre $g$, que l’on suppose triangulée (c’est-à-dire munie d’une décomposition polyèdrale dont toutes les faces sont des triangles). On note $S$, $A$, $F$ les nombres de sommets, arêtes et faces (i.e. triangles) de la triangulation. D’après le corollaire ci-dessus, on a donc

$$2-2g = \chi(\Sigma) = S-A+F.$$

Comme $\Sigma$ est une surface sans bord, toute arête appartient à exactement 2 faces, et chaque face contient exactement 3 arêtes. Ainsi $2A=3F$ d’où $S-\chi(\Sigma)= A/3$. Par ailleurs, dans une triangulation, deux sommets (distincts) déterminent au plus une arête et donc $A\leq S(S-1)/2$. On en déduit que

$$7S-6\chi(\Sigma)\leq S^2,$$

c’est-à-dire

$$(S-7/2)^2 \geq \big( 49/4 -6\chi(\Sigma)\big) = \frac{1}{4}\big( 1+48g\big).$$

On en déduit finalement la borne suivante sur le nombre de sommets d’une triangulation de $\Sigma$ :

$$S\,\geq \,\frac{1}{2}\Big( 7+\sqrt{1+48g}\Big).$$

En particulier, $S\geq 4$ pour la sphère, $S\geq 7$ pour le tore.