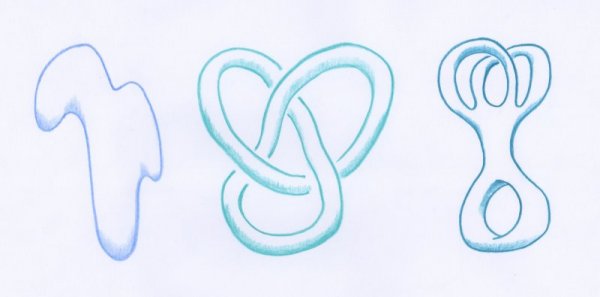La théorie de Morse, de la topographie à la conjecture de Poincaré en grande dimension

Ce texte est basé sur l’article intitulé « De la topographie à la géométrie », publié en deux parties par Patrick Popescu-Pampu sur le site Images des Mathématiques en 2016, à paraître aussi dans l’ouvrage « La carte invente le monde » de la collection Les nouveaux Rendez-vous d’Archimède, Presses Universitaires du Septentrion, 2018.

À propos des cartes topographiques

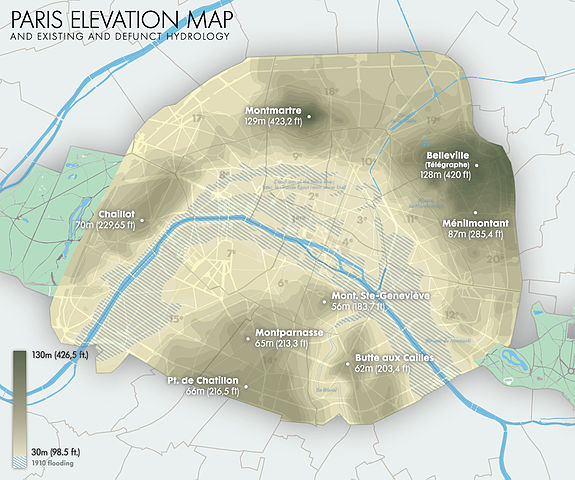
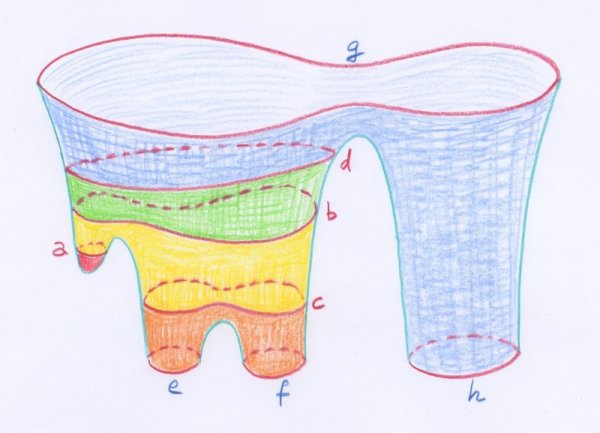
Saviez-vous que Paris est une ville à huit collines ? Voici une carte qui permet de le vérifier :

La ville aux huit collines.

On peut y voir les noms de ces collines, ainsi que leurs altitudes. Mais on observe aussi un dégradé de couleurs, les plus sombres correspondant aux niveaux les plus élevés. La frontière entre deux régions de couleurs différentes est une ligne d’altitude constante. Une carte sur laquelle sont représentées de telles lignes est dite « topographique » — du grec « topos » (lieu) et « graphein » (dessiner).

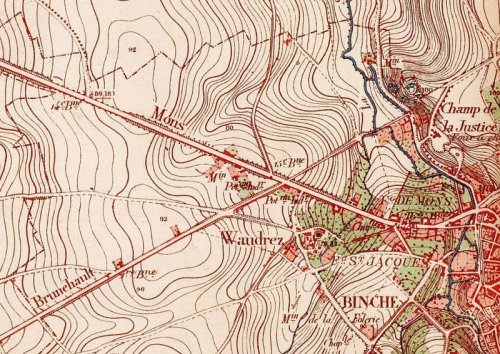
En voici une autre dans laquelle la collection des lignes d’altitude constante est enrichie par des informations concernant les routes, les bâtiments et les communes :

Une carte topographique enrichie d’informations supplémentaires.

Comment construit-on une carte de ce type ? Le principe théorique est de représenter d’abord le paysage par une surface lisse, obtenue en gommant les anfractuosités trop prononcées — comme par l’effet d’une chute de neige suffisamment importante. On coupe ensuite cette surface par des plans « horizontaux », pris successivement à la même distance les uns des autres, puis on projette les courbes obtenues sur un même plan horizontal. Ce processus est illustré dans la figure suivante :

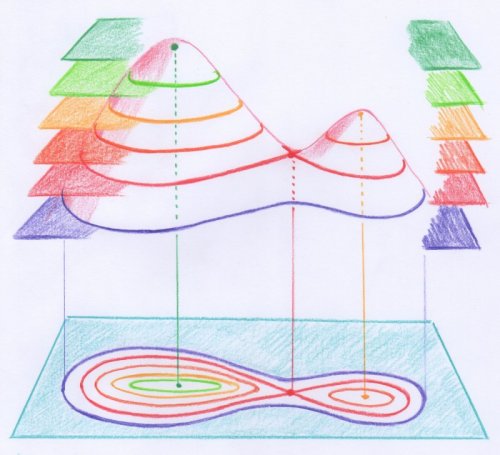
Principe de construction d’une carte topographique, illustré à l’aide d’une surface lisse représentant un paysage à deux collines.

Bien sûr, la Terre n’étant point plate, la notion de plan « horizontal » n’est pas bien définie. Mais l’idée est que ces courbes d’intersection sont proches de lignes d’altitude constante, raison pour laquelle leurs projections sont appelées « lignes de niveau ». Attention : l’intersection de la surface lisse qui représente le paysage avec un plan horizontal est composée en général de plusieurs parties d’un seul tenant ou, comme les appellent les mathématiciens, des « composantes connexes ». Ici une « ligne de niveau » désigne l’une de ces composantes connexes.

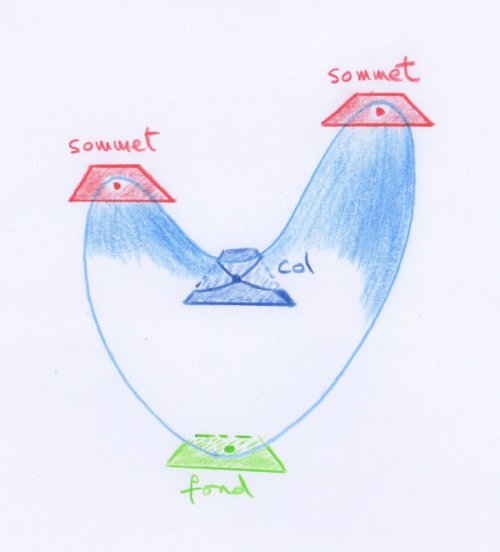
Dans sa version la plus simple, qui n’utilise pas de couleurs, une carte topographique est une telle collection de lignes de niveau. La plupart d’entre elles sont des courbes simples lisses, mais certaines sont réduites à des points — les sommets et les fonds — et d’autres se recoupent elles-mêmes. Dans la figure précédente, c’est le cas pour celle obtenue en prenant le plan qui passe par le col, c’est-à-dire le deuxième plan horizontal, en partant du bas.

Le but de cet article est d’expliquer comment la réflexion sur la structure des cartes topographiques a conduit à l’un des outils les plus puissants pour comprendre la topologie des variétés : la théorie de Morse.

Quelques réflexions de Cayley

Notre histoire démarre en 1859, lorsque le mathématicien britannique Arthur Cayley écrivit un article [1] dans lequel il s’interrogea sur les formes possibles des lignes de niveau, et sur leur changement qualitatif lorsque l’on varie l’altitude :

Il s’agit, je pense, d’une question intéressante de topographie, de considérer la configuration générale d’un système de lignes de niveau et de lignes de plus grande pente. Imaginez, pour fixer les idées, une île montagneuse, la ligne de niveau extérieure ou de la mer étant par conséquent une courbe fermée ; le cas où il existe des lignes de niveau qui se recoupent elles-mêmes est important, et il sera considéré [...].

La ligne de contour qui borde une élévation peut rapetisser indéfiniment et finalement se réduire à un point, qui est un sommet ; la ligne de niveau qui borde une dépression peut de même rapetisser indéfiniment et se réduire finalement à un point, que j’appelle un immet.

[...] il y a aussi, comme en un col, des points où la surface est horizontale, mais où l’élévation n’est ni un maximum, ni un minimum ; on descend en arrière et en avant, mais on monte à droite et à gauche : j’appellerai ici ce genre de point un nœud.

Par exemple, dans le dessin précédent il y a deux « sommets », un « nœud », mais aucun « immet ». Par la suite, j’écrirai « fond » plutôt qu’« immet ».

Les « sommets », les « nœuds » et les « fonds » sont appelés les « points singuliers » de la carte topographique [2]. Au voisinage des autres points, que les mathématiciens ont l’habitude d’appeler « points généraux » de la carte, les lignes de niveau ont l’aspect d’une famille de droites parallèles un peu déformées :

Aspect qualitatif des lignes de niveau au voisinage d’un point général, d’un sommet ou d’un fond, et enfin d’un nœud.

Afin de mieux comprendre en quoi l’étude de Cayley est « qualitative » — non pas « quantitative » — regardons la figure suivante :

Les deux sortes de lignes de niveau qui passent par un nœud, lorsque le paysage est suffisamment général.

Cayley explique que pour un paysage suffisamment général — qui n’est pas trop particulier, au sens où on demande que les seuls points singuliers de la carte topographique associée soient des trois types précédents et qu’il n’y ait pas deux cols à la même altitude — toute ligne de niveau qui se referme tout en se recoupant elle-même est de l’une de ces deux sortes. Dans les deux cas, la ligne de niveau contient un seul « nœud » et deux boucles. La différence entre ces deux situations est que pour la première les boucles sont extérieures l’une de l’autre [3], et pour la deuxième l’une des boucles est entourée par l’autre [4].

Nous avons vu une ligne de niveau du premier type dans la carte topographique du paysage à deux collines dessiné précédemment. Quant à la situation où l’une des boucles contient l’autre, elle peut se produire par exemple lorsque l’on coupe par le plan horizontal qui passe par le col permettant d’entrer dans le cratère d’un volcan :

Un cratère de volcan. On trouve un col à droite sur l’image.

Un exemple de ligne de niveau passant par un col, dont une boucle contient la seconde.

Cette description des lignes de niveau passant par les nœuds est « qualitative » et non pas « quantitative », car l’on ne s’intéresse qu’à l’agencement mutuel des deux boucles, en négligeant leur taille et leur courbure.

Pour des paysages particuliers il est possible d’avoir des lignes de niveau qui se recoupent elles-mêmes de manière plus compliquée, en contenant plusieurs nœuds — si plusieurs cols se trouvent à la même altitude — ou bien en ayant des points singuliers par lesquels la courbe passe plus de deux fois :

Une courbe fermée qui se recoupe elle-même quatre fois, mais en seulement deux points.

Mais Cayley remarque que tout paysage se ramène au cas général décrit précédemment par une petite perturbation de la surface qui le représente. Dans la nature, une telle perturbation peut être due par exemple à l’érosion. Ainsi, même si à un moment donné de l’histoire deux cols ont la même altitude, l’érosion les placera avec le temps à des hauteurs différentes.

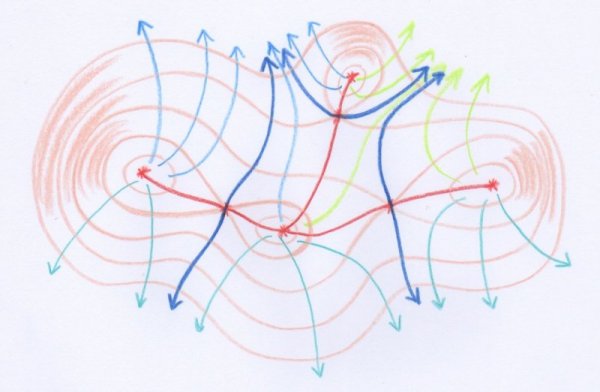
Pour le moment nous avons parlé seulement des lignes de niveau. Mais dans le texte de Cayley il est aussi question de « lignes de plus grande pente ». Celles-ci sont les projections des courbes tracées sur le paysage, le long desquelles la montée ou la descente est la plus abrupte possible. Quelques-unes sont illustrées en bleu dans la figure suivante, qui correspond au même paysage à deux collines qu’auparavant :

Lignes de niveau et lignes de plus grande pente.

Cayley considère que la connaissance des lignes de plus grande pente passant par les nœuds est particulièrement importante pour comprendre comment s’écoule l’eau sur ce paysage :

Les lignes de plus grande pente passant par un nœud peuvent être appelées ligne de faîte et ligne d’écoulement [...].

La ligne de faîte, définie précédemment, détermine la ligne de partage des eaux. [...] dans le cas d’une chaîne de sommets montagneux, la ligne de partage des eaux court de sommet en sommet à travers les cols, c’est-à-dire qu’elle est constituée d’une série de lignes de faîte, chacune s’étendant de sommet en sommet à travers un nœud. Et les lignes d’écoulement sont, aussi près que cela est possible, les lits des torrents qui s’écoulent des cols vers les vallées latérales.

Dans la figure suivante nous avons dessiné une carte topographique d’un paysage insulaire un peu plus compliqué que le précédent, ayant cette fois-ci quatre collines. Nous invitons le lecteur à y reconnaître les « lignes de niveau », les « lignes de faîte », les « lignes de plus grande pente » et les « lignes d’écoulement » :

Lignes de niveau, lignes de plus grande pente, lignes de faîte et bassins.

On pourra remarquer que les lignes de partage des eaux — c’est-à-dire les lignes de faîte — divisent le paysage en bassins. Il y a changement brusque de bassin lorsqu’on traverse une telle ligne, mais l’on passe continûment d’un bassin à l’autre lorsque l’on fait le tour de l’île, le long de son rivage.

Möbius et le découpage des surfaces en tranches

Peu après Cayley, en 1863, le mathématicien et astronome allemand August Ferdinand Möbius écrivit un article [5] dans lequel il découpa lui aussi des surfaces par des plans parallèles entre eux. On y trouve une différence importante par rapport à l’article de Cayley : ces surfaces ne représentaient pas un paysage, mais elles étaient refermées sur elles-mêmes, comme une sphère ou un tore. Autrement dit, Möbius considérait des surfaces fermées.

Quelques exemples de surfaces fermées.

Le but de Möbius était de classifier les surfaces fermées à homéomorphisme près. Autrement dit, il voulait décrire une liste de surfaces, telle que toute surface fermée soit homéomorphe à une surface de cette liste, et telle que deux surfaces différentes dans la liste ne soient jamais homéomorphes. On obtiendrait ainsi une sorte d’atlas zoologique des surfaces fermées, complet au sens où tous les « animaux » possibles y seraient représentés.

Avant de voir comment Möbius procéda, et pour se faire une intuition des difficultés posées par le problème, observons quelques figures. On peut montrer que les trois surfaces de la figure ci-dessus ne sont pas homéomorphes. Intuitivement, elles n’ont pas le même nombre de « trous » [6]. Dans la figure ci-dessous sont représentées plusieurs surfaces homéomorphes à une sphère ronde usuelle — on écrira simplement par la suite, que ce sont toutes des « sphères » :

Quelques sphères, au sens topologique.

Et dans la figure suivante sont représentées des surfaces homéomorphes à un tore de révolution (une bouée) — on écrira de même simplement qu’il s’agit de « tores » :

Quelques tores, au sens topologique.

Möbius aborda la classification des surfaces sous un angle topographique. En effet, son approche consista à partir d’une surface donnée et à la couper par des plans parallèles, pensés comme étant « horizontaux ». On a vu qu’en perturbant un peu la surface qui représente un paysage, elle peut se ramener à une surface générale au sens de Cayley. En fait, cela est vrai aussi des surfaces fermées considérées par Möbius [7]. C’est-à-dire qu’en les déformant légèrement, on peut les ramener à des surfaces qui n’ont plus que des sommets, des fonds et des cols comme points où le plan tangent est horizontal, et telles que, de plus, il n’y ait pas deux cols situés à la même hauteur. Voici une illustration d’une telle surface fermée en position générale par rapport aux plans horizontaux :

Une sphère en position générale par rapport aux plans horizontaux.

Möbius choisit ensuite un nombre fini de plans horizontaux de telle manière que :

• ces plans ne soient jamais tangents à la surface, c’est-à-dire qu’ils ne passent pas par ses sommets, ses fonds ou ses cols ;
• entre deux plans consécutifs il n’y ait qu’un seul sommet, fond ou col.

Voici un tel choix de plans, pour la sphère de la figure précédente :

Un choix de plans à la Möbius.

Il est toujours sous-entendu que la collection de plans est enrichie par un plan situé en dessous de tous les autres, ne coupant pas la surface, et d’un plan analogue situé au dessus de tous les autres. La contrainte concernant les plans consécutifs est imposée à cette collection enrichie.

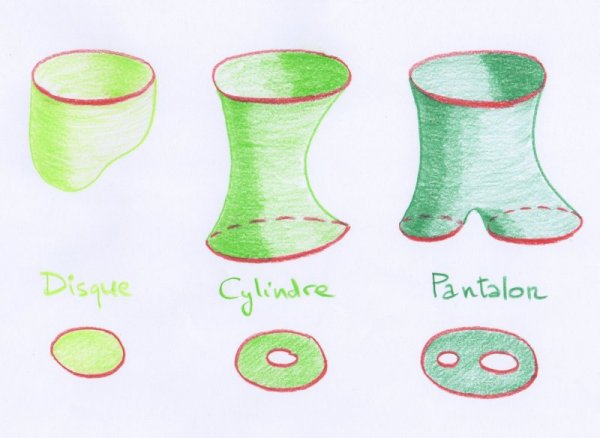
Dans ce cas, les composantes connexes (c’est-à-dire les morceaux d’un seul tenant) de chaque tranche de surface comprise entre deux plans consécutifs ne peuvent être que des types suivants :

• soit un disque, dont le bord est composé d’un seul cercle ;
• soit un cylindre, dont le bord est composé de deux cercles ;
• soit un pantalon, dont le bord est composé de trois cercles.

Les surfaces élémentaires apparaissant par la méthode de découpage de Möbius.

Ces noms sont à prendre à la manière des topologues, qualitativement. C’est-à-dire qu’un « disque » désigne une surface homéomorphe à un disque plan au sens usuel, et ainsi de suite. De même, nous appellerons « cercle » toute courbe homéomorphe à un cercle rond au sens usuel.

On pourra vérifier que la sphère dessinée précédemment est découpée par sa collection de plans horizontaux en trois disques, un cylindre et un pantalon.

Le calcul topologique de Möbius

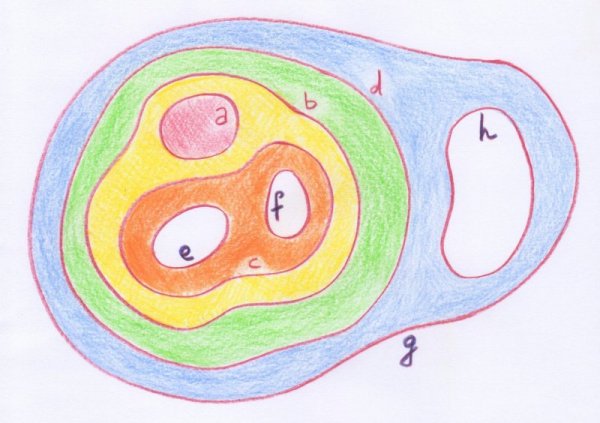
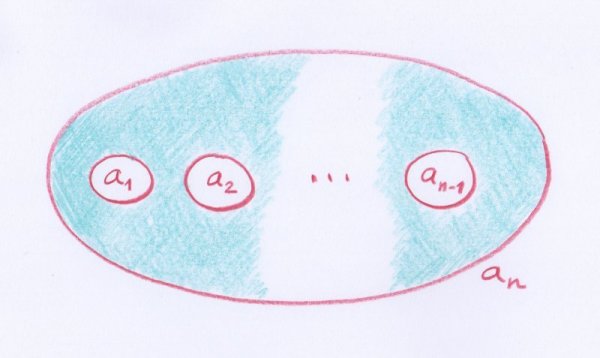
Remarquons que le bord d’un disque est formé d’un cercle, celui d’un cylindre de deux cercles et enfin celui d’un pantalon de trois cercles. Pour retenir de quelle forme est chaque morceau, il suffit donc de retenir combien de cercles composent son bord. Möbius fit un peu plus, afin de retenir aussi la manière dont ces disques, cylindres et pantalons sont recollés entre eux. Il donna un nom — simplement une lettre — à chaque cercle produit en intersectant la surface avec l’un des plans choisis, et il coda chaque morceau de surface en écrivant entre parenthèses les noms des cercles qui constituent son bord. Il coda ensuite la surface entière par la somme des termes associés aux morceaux.

Voici un exemple tiré de son article :

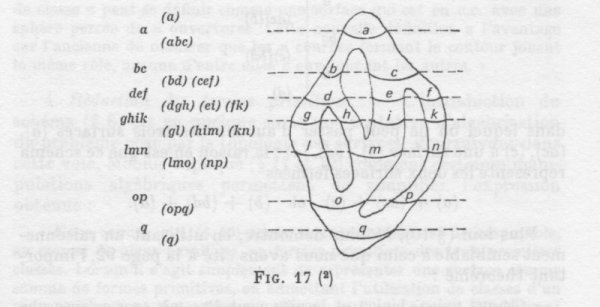
L’un des exemples de Möbius. On voit les différents morceaux en lesquels se retrouve découpée la surface initiale, ainsi que leurs codages.

Ce découpage en tranches est codé par la somme suivante :

$$ (a) + (abc) + (bd) + (cef) + (dgh) + \\ + (ei) + (fk) + (gl) + (him) + (kn) + (lmo) + (np) + (opq) + (q).$$

Möbius introduisit deux règles de calcul permettant de transformer de telles sommes tout en conservant au sens qualitatif la forme de la surface qu’elles représentent. Ces règles, qui modifient de $\pm 1$ le nombre de termes de la somme, sont inverses l’une de l’autre. Il suffit donc de décrire une seule d’entre elles. Voici celle qui permet de diminuer le nombre de termes :

• si deux termes ont exactement une lettre en commun, alors on remplace leur somme par le terme obtenu en prenant les lettres apparaissant dans les deux termes, à l’exception de la lettre commune ; par exemple, $(cd) + (cef) = (def)$.

Illustrons l’utilisation répétée de cette règle sur les cinq premiers termes de la somme précédente :

$$\begin{array}{c} (a) + (abc) + (bd) + (cef) + (dgh) = \\ = (bc) + (bd) + (cef) + (dgh) = \\ = (cd) + (cef) + (dgh) = \\ = (def) + (dgh) = \\ = (efgh). \end{array} $$

Ce calcul reflète dans le monde de l’algèbre le fait géométrique qu’en recollant les cinq morceaux de surface correspondants, on obtient un pantalon à tripèdes, comme illustré sur la figure suivante :

La surface qui correspond à la somme $(a) + (abc) + (bd) + (cef) + (dgh)$.

Pour reconnaître dans cette surface un pantalon à tripèdes, c’est-à-dire un pantalon muni de trois jambes, il faut imaginer que le pantalon est vu du haut, de l’ouverture principale par laquelle passe le corps, les ouvertures pour les trois jambes du tripède apparaissant comme des trous. En vision latérale on aurait plutôt :

La même surface, mais vue de biais. Un être à trois jambes — un tripède — pourrait l’utiliser comme pantalon.

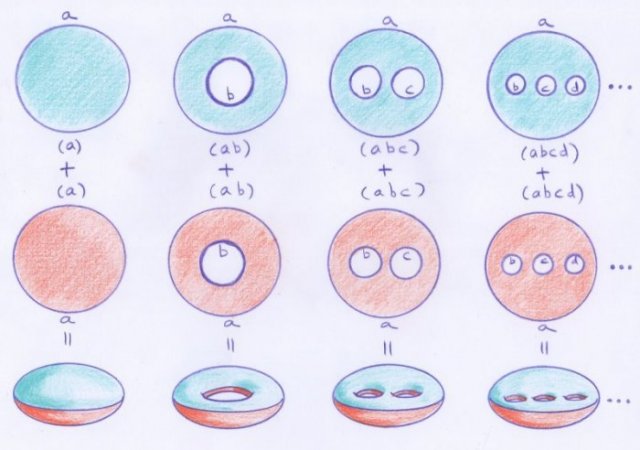
Notons qu’en procédant de la sorte, Möbius se permet de travailler avec des surfaces codées par un nombre quelconque de lettres, pas seulement par une, deux ou trois, comme c’était le cas pour les disques, cylindres et pantalons du découpage initial. S’il y a $n$ lettres, donc si le code est $(a_1 a_2 \dots a_n)$, alors la surface représentée est homéomorphe à un disque privé de $n-1$ disques plus petits, comme sur la figure suivante :

La surface dont le code est $(a_1 a_2 \dots a_n)$.

Revenons au calcul précédent.

En procédant de la même manière avec les termes restants dans la somme de l’exemple de Möbius, mais en partant de la fin, on obtient :

$$\begin{array}{c} (ei) + (fk) + (gl) + (him) + (kn) + (lmo) + (np) + (opq) + (q) = (efgh). \end{array} $$

En combinant cette égalité et la précédente, on voit que la somme correspondant au découpage de départ est égale à la somme suivante (c’est-à-dire qu’elle peut se ramener à celle-ci par utilisation répétée de la règle de calcul de Möbius) :

$$(efgh) + (efgh).$$

Plus généralement, Möbius montra que toute surface fermée de l’espace usuel est homéomorphe [8] à l’une des surfaces suivantes :

Les quatre premières surfaces fermées de la classification de Möbius.

De plus, il est possible de montrer que ces surfaces sont deux à deux distinctes du point de vue topologique, c’est-à-dire qu’elles sont deux à deux non homéomorphes [9].

C’est de la sorte que Möbius classifia, à homéomorphisme près, les surfaces fermées de l’espace usuel. Sa preuve utilise les deux règles de calcul, et pas seulement celle énoncée plus haut, qui diminue le nombre de termes. En effet, il est possible qu’en appliquant uniquement cette dernière, on se retrouve bloqué sans être parvenu à une somme de deux termes identiques. Dans ce cas, il faut recourir à la règle inverse, afin de débloquer la situation.

Remarquons un aspect important de la preuve de Möbius : elle montre que la surface initiale est homéomorphe abstraitement à l’une des surfaces de la liste précédente. Mais l’homéomorphisme entre les deux surfaces fourni par cette preuve ne s’étend pas nécessairement à l’espace ambiant. Par exemple, on peut montrer que le tore noué du centre de la figure qui illustre la notion de surface fermée est homéomorphe à un tore de révolution usuel — la surface codée par la somme $(ab) + (ab)$ — mais qu’il n’existe pas d’homéomorphisme entre ces deux surfaces qui s’étende à l’espace ambiant.

À l’époque de Möbius on était loin d’avoir les techniques nécessaires pour prouver un tel résultat. Möbius a été en fait un pionnier des techniques de calcul algébrique avec des portions d’espace [10], qui allaient permettre aux mathématiciens du XXe siècle de formuler de tels problèmes, et de les résoudre dans bien des cas.

Dans cet article, nous expliquons plus formellement comment classifier les surfaces grâce aux idées de Möbius. On peut également classifier les surfaces en utilisant d’autres types de décompositions. Nous expliquons notamment ici et ici comment classifier les surfaces à l’aide de triangulations.

Une reformulation du théorème de classification des surfaces fermées

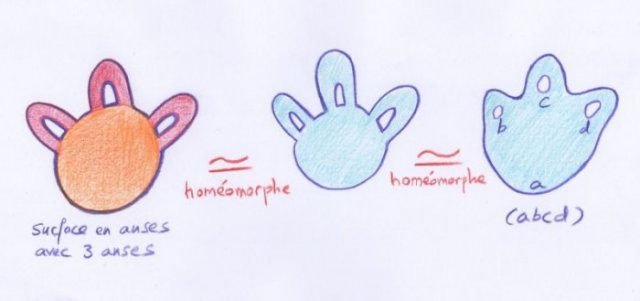
On peut aussi présenter les surfaces fondamentales $(a)$, $(ab)$, $(abc), ...$ comme des « surfaces en anses », obtenues à partir de disques en leur recollant des « anses » quadrilatérales :

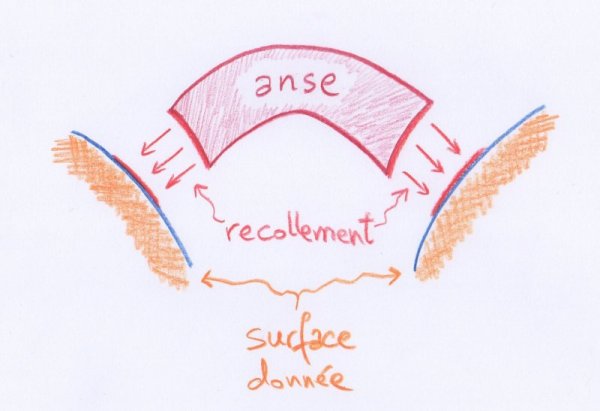
Recollement d’une anse à une surface. L’anse est homéomorphe à un disque, mais elle est pensée comme étant un quadrilatère : le recollement se fait le long de deux côtés opposés de son bord.

Le dessin suivant illustre le fait qu’une surface de type $(abcd)$, c’est-à-dire un « pantalon à tripède », est homéomorphe à une surface en anses ayant $3$ anses :

Surfaces homéomorphes à une surface obtenue en recollant trois anses à un disque.

Attention, la réciproque n’est pas correcte. En effet, on peut recoller trois anses à un disque et ne pas obtenir un pantalon à tripède :

Ceci n’est pas un pantalon à tripède. En effet, le bord de cette surface n’est composé que de deux cercles, et non pas de quatre.

Le théorème de Möbius peut donc se reformuler de la manière un peu plus faible suivante :

Cet énoncé est un peu plus faible que celui démontré par Möbius parce que parler juste de « surfaces en anses » ne précise pas desquelles il s’agit.

En fait, la technique de preuve de Möbius s’applique à toutes les surfaces fermées, pas seulement à celles qui vivent dans l’espace de dimension trois. Avec un bémol : il faut partir de surfaces orientables. On n’avait pas à préciser cette condition dans le cas considéré par Möbius, car toute surface fermée de l’espace tridimensionnel est orientable, comme nous l’expliquons ici. Cela cesse d’être le cas pour les surfaces qui vivent dans des espaces de dimension plus grande.

Les scindements de Heegaard

Le mathématicien danois Poul Heegaard prouva dans sa thèse de 1898 [11] un analogue du théorème de classification des surfaces énoncé dans la section précédente pour les variétés de dimension $3$ :

Mais qu’est-ce donc qu’un « corps en anses » ? En voici un, avec trois anses :

Un corps en anses avec trois anses.

De même qu’une « surface en anses » est obtenue à partir d’un disque en collant des bandes quadrilatérales sur le bord de ce disque, un « corps en anses » s’obtient à partir d’une boule en recollant des tubes cylindriques pleins sur le bord de cette boule. On obtient une variété à bord de dimension $3$ qui est (à homéomorphisme près) une « fougasse à $g$ trous », où $g$ est le nombre de cylindres qu’on a collés.

Aujourd’hui, on parle d’une décomposition ou d’un scindement de Heegaard pour désigner un découpage d’une variété fermée de dimension $3$ en deux corps en anses.

Comme pour les surfaces, un problème de base concernant les variétés fermées de dimension $3$ est leur classification qualitative, à homéomorphisme près. On pourrait essayer de faire cette classification par analogie avec celle décrite précédemment pour les surfaces, en utilisant le théorème de Heegaard. Plusieurs difficultés rendent cette approche très malaisée. Voici deux d’entre elles :

• Le recollement des bords de deux corps en anses est loin d’être unique [12].

• Le nombre d’anses des deux corps en anses qui permettent d’obtenir une variété de dimension trois donnée n’est pas bien défini [13]

C’est entre autres pour ces raisons que le monde des formes qualitatives des variétés de dimension trois est beaucoup plus compliqué que celui des surfaces ! En particulier, on ne peut pas faire une liste simple des formes possibles de ces variétés, comme celle obtenue par Möbius dans sa classification des surfaces orientables. Cela explique partiellement pourquoi l’étude de la structure topologique des variétés de dimension trois reste très active. Et les scindements de Heegaard font toujours partie des outils importants pour cette étude ! [14].

En immergeant un col, on rajoute une anse

Arrivés à ce point, on semble s’être éloignés des cartes topographiques et de leurs lignes de niveau. Qu’est-ce que celles-ci ont à voir avec les corps en anses ? Pour le comprendre, revenons aux surfaces représentant un paysage. Nous allons voir que les anses correspondent au passage d’un col.

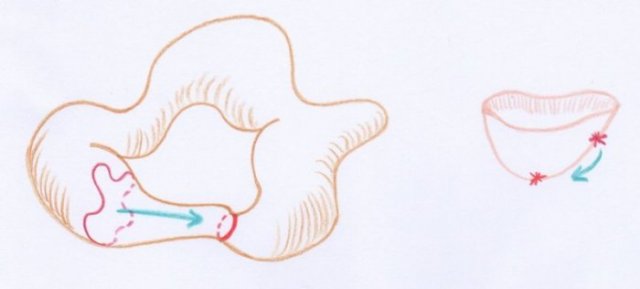
Considérons à nouveau le paysage initial à deux collines, que nous concevrons comme étant celui d’une île. Imaginons alors que le niveau de l’eau monte jusqu’à dépasser le niveau du col :

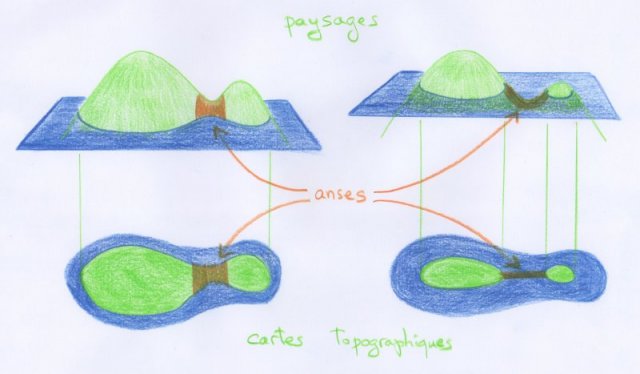
Lorsque le niveau de l’eau monte et passe au-dessus d’un col, la partie immergée change qualitativement par le rajout d’une anse. De même, lorsque le niveau de l’eau baisse en passant en dessous d’un col, la partie émergée change aussi par le rajout d’une anse.

On constate que la partie immergée a changé qualitativement par le rajout d’une anse ! Il est intéressant de constater que la partie émergée change elle aussi par rajout d’une anse, pourvu que l’on regarde ce qui se passe lorsque l’eau baisse.

Soyons un peu plus explicites. Dans les quatre dessins qui précèdent, la partie assombrie est une anse. Son positionnement change lorsque l’on regarde l’île immergée (à droite) ou dégagée des eaux (à gauche), mais qualitativement elle est placée de la même manière. On peut constater qu’en la rajoutant aux deux îlots des dessins de droite, on obtient qualitativement la décomposition des dessins de gauche.

On a une situation analogue lorsque l’on passe un col d’une fonction hauteur sur une variété de dimension $3$ : cela correspond au rajout d’une anse tubulaire. Nous donnons ici une preuve du théorème de Heegaard basée sur ces idées, et là une preuve basée sur un argument complètement différent.

Un point de vue unificateur

En fait, considérer des fonctions définies sur des variétés de dimension quelconque permet d’obtenir un cadre commun pour les situations décrites jusqu’à présent : la construction d’une carte topographique, la classification à la Möbius des surfaces fermées de l’espace usuel et la décomposition à la Heegaard des variétés fermées de dimension trois. En effet, dans les trois cas on est en présence :

• d’une variété : le plan horizontal sur lequel se fait la carte topographique d’un paysage donné, la surface fermée chez Möbius et la variété de dimension trois de départ chez Heegaard ;
• d’une fonction à valeurs réelles définie sur cette variété : l’altitude du paysage dans le cas de la construction d’une carte topographique, la hauteur au-dessus d’un plan fixé pour la situation considérée par Möbius et enfin une fonction à valeurs réelles dans la situation de Heegaard [15].

Pour la fonction hauteur d’une carte topographique, et plus généralement pour une fonction sur une variété de dimension 2, nous avons vu qu’il apparait trois types de points singuliers : les sommets, les cols et les fonds. Sur une variété de dimension arbitraire, la diversité des points singuliers qui peuvent apparaitre est beaucoup plus grande. Comprendre comment classer ces points singuliers selon leur type est essentiel pour aboutir, à partir d’eux, à une décomposition de la variété analogue aux décompositions de Möbius ou de Heegaard.

C’est le mathématicien américain Marston Morse qui fit cette étude des points singuliers en dimension quelconque. Il était motivé par des problèmes concernant l’existence de géodésiques fermées.

Les problèmes de géodésiques

Que sont les « géodésiques » ? Il s’agit d’analogues des droites dans le plan ou l’espace de la géométrie euclidienne, mais vivant dans n’importe quel espace pour lequel on peut parler de la distance entre deux points — nous dirons alors, comme il est d’usage en mathématiques, que la variété est munie d’une « métrique ».

Plus précisément, les géodésiques sont les courbes qui réalisent le plus court chemin entre deux quelconques de leurs points, pourvu que ceux-ci soient suffisamment proches le long de la courbe.

Pour comprendre cette dernière condition, qui est un peu subtile, considérons les géodésiques sur une sphère au sens usuel de l’espace euclidien. On peut montrer que ce sont exactement les grands cercles tracés sur celle-ci, analogues de l’équateur sur un globe terrestre. Autrement dit, ce sont les cercles obtenus en intersectant la sphère avec un plan qui passe par son centre.

Fixons un grand cercle, puis considérons deux points dessus, qui ne soient pas diamétralement opposés. Un tel choix est illustré dans la figure suivante :

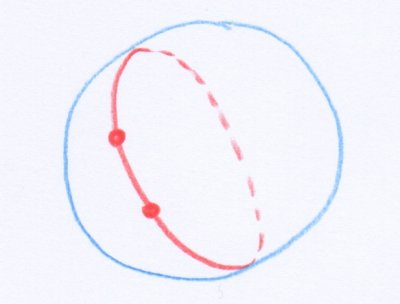
Un grand cercle sur une sphère au sens usuel, et deux de ses points qui ne sont pas diamétralement opposés.

Les deux points décomposent le grand cercle en deux arcs. Visiblement, l’arc le plus long ne réalise pas le plus court chemin entre les deux points. La raison en est que les points ne sont pas suffisamment proches le long de cet arc.

Les problèmes fondamentaux concernant les géodésiques dans une variété donnée $V$ munie d’une métrique sont les suivants :

• montrer qu’il existe beaucoup de géodésiques fermées ;
• montrer qu’il existe beaucoup de géodésiques reliant deux points donnés.

De même que dans le cas des travaux de Möbius et de Heegaard discutés plus haut, on peut penser à ces problèmes par analogie avec l’étude topographique d’un paysage. Mais cette fois-ci il s’agit d’un paysage vivant sur une variété de dimension infinie. En effet :

• Les « points » de la variété qui est le support du paysage sont les courbes déformables continûment en une courbe donnée de $V$, soit parmi les courbes fermées, soit parmi les courbes qui relient deux points donnés. Nous dirons qu’il s’agit de la variété des chemins du problème de géodésiques considéré.
• La valeur de la fonction hauteur en un point de la variété des chemins est égale à la longueur de la courbe associée.
• Les points singuliers de cette fonction hauteur sont précisément les géodésiques !

Mais, à la différence des situations considérées auparavant, la variété des chemins est de dimension infinie, dès que la variété $V$ est de dimension au moins deux.

Une explication

Pour se convaincre — si besoin est — de cela, considérons un « point » quelconque dans la variété des chemins. Il s’agit d’une courbe $\gamma$ dans $V$ (plus précisément, il s’agit soit d’une courbe fermée, soit d’une courbe reliant deux points donnés de $V$). Choisissons un nombre $n$ arbitrairement grand de points sur la courbe $\gamma$, puis des petits voisinages deux à deux disjoints de ces points. Comme $V$ est de dimension au moins deux, on peut déformer $\gamma$ dans chacun de ces voisinages, à chaque fois avec un degré de liberté. Cela est illustré sur la figure suivante :

Illustration de l’existence d’au moins trois degrés de liberté indépendants pour la déformation de cette courbe, pourvu que la variété ambiante soit de dimension au moins deux.

Ces déformations pouvant être faites indépendamment l’une de l’autre, on obtient en tout $n$ degrés de liberté. Donc la variété des chemins est de dimension au moins $n$. Comme $n$ peut être pris arbitrairement grand, il résulte de cela que la dimension recherchée est infinie.

Il s’agit de l’un des exemples fondamentaux qui ont obligé les mathématiciens à développer une intuition géométrique et des techniques de travail pour étudier des objets vivant dans des espaces de dimension infinie.

Revenons à la variété des chemins sur une variété donnée munie d’une métrique. La méthode la plus simple pour montrer l’existence d’une géodésique fermée est la « méthode de minimisation ». Elle consiste à raccourcir petit à petit la courbe fermée de départ jusqu’à ce qu’elle aboutisse à une courbe réalisant le minimum de la longueur :

La méthode de minimisation.

À gauche de la figure précédente est représenté un tel processus sur un tore gondolé de l’espace euclidien usuel. À droite est représentée une situation analogue sur une surface — dont les points sont vus comme des analogues des courbes sur le tore. Sur cette surface, on peut aboutir à un fond en y faisant descendre suffisamment un point de départ donné.

On peut montrer que cette méthode marche chaque fois que l’on part d’une courbe fermée qui ne se déforme pas continûment en un point. C’était le cas de la courbe tracée sur le tore de la figure précédente. Mais sur une surface homéomorphe à une sphère — que nous appellerons simplement une « sphère » dans ce qui suit — toute courbe fermée se déforme continûment en un point. La méthode précédente ne marche donc pas. Que faire ?

La méthode du mini-max de Birkhoff

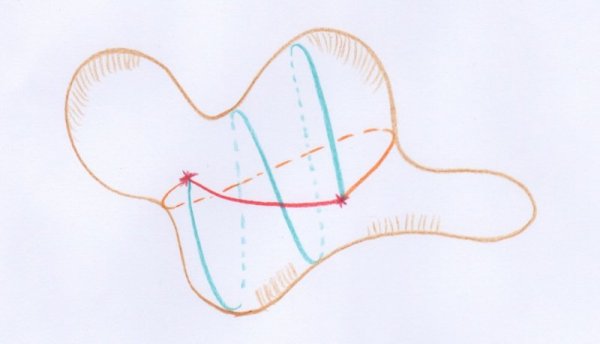
Le mathématicien américain George Birkhoff imagina dans ce cas une nouvelle méthode, dite du « mini-max », dans un article [16] publié en 1917.

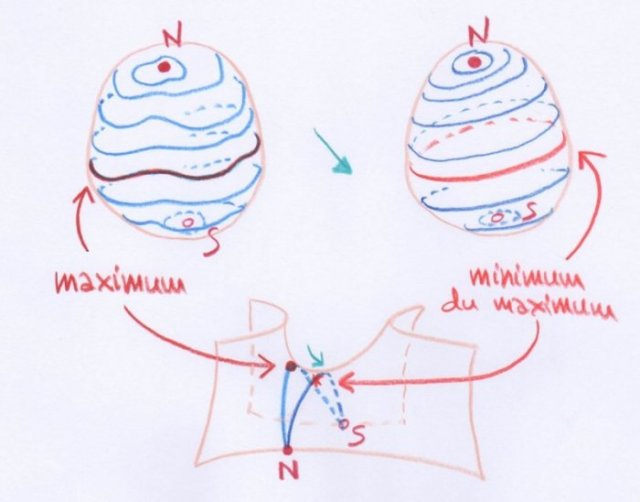
Cette méthode consiste à parcourir les étapes suivantes, en partant d’une sphère sur laquelle on sait mesurer les distances entre les points :

• on fixe deux points distincts $S$ et $N$ sur la sphère, pensés comme ses pôles ;
• on considère des familles de courbes fermées qui vont d’un pôle à l’autre, de la même manière que les cercles de latitude constante (les parallèles) vont d’un pôle à l’autre sur le globe terrestre ;
• pour chaque famille de ce type, on considère une courbe qui réalise le maximum des longueurs des courbes qui en font partie (c’est-à-dire, la courbe la plus longue de la famille ; s’il y en a plusieurs, on en choisit une) ;
• parmi toutes les familles de ce type qui vont d’un pôle à l’autre, on en prend une pour laquelle ce maximum est minimal (c’est-à-dire, pour laquelle la plus longue courbe de la famille est la plus courte lorsque l’on varie la famille) ;
• il s’avère qu’une telle courbe qui minimise le maximum des longueurs atteintes dans de telles familles est une géodésique ! C’est à cette recherche d’un minimum du maximum que la méthode doit son nom.

Ce processus est illustré dans la partie supérieure de la figure suivante :

La méthode du mini-max de Birkhoff.

Dans la partie inférieure est illustrée une situation analogue sur une surface munie d’une fonction hauteur, comme celle des articles de Cayley ou Möbius, mesurant l’altitude par rapport à un plan horizontal. On considère deux points $S$ et $N$ de la surface situés au même niveau et diverses courbes qui les relient en passant au voisinage d’un col. Si on cherche à minimiser l’altitude maximale atteinte lorsqu’on parcourt un tel chemin, alors on est obligés de passer par le col !

La géodésique obtenue à la fin de la méthode de Birkhoff est donc l’analogue du col sur la surface. Il est possible que la méthode fournisse plusieurs géodésiques. Cela veut simplement dire que le paysage décrit par la fonction longueur sur la variété des chemins est qualitativement plus compliqué — il a plusieurs cols — que la surface du dessin précédent.

L’exemple de la surface indique aussi que les points singuliers d’une fonction hauteur sur une variété qui sont détectés par la méthode du mini-max de Birkhoff, sont des généralisations des cols ou des nœuds. Nous les appellerons par la suite points de mini-max.

Birkhoff appliqua la méthode du mini-max aux points de la variété des chemins, qui est de dimension infinie, comme nous l’avons vu précédemment.

Pour étudier en profondeur des espaces de dimension infinie, il est souvent commode de les voir comme des limites de suites de variétés de dimensions finies, mais tendant vers l’infini. Ce point de vue a poussé les mathématiciens à développer de nouveaux outils d’étude qualitative des variétés de dimension finie quelconque. Nous verrons maintenant que de tels outils peuvent être construits eux aussi à partir des fonctions définies sur ces variétés.

L’inégalité du mini-max de Birkhoff

Considérons une variété fermée $V$ de dimension finie quelconque, et une fonction lisse $f$ définie sur $V$. Introduisons les notations suivantes :

• $M_0$ = nombre de minima locaux de la fonction $f$ ;
• $M_1$ = nombre de points de mini-max de $f$ ;
• $C_0$ = nombre de composantes connexes de la variété $V$ ;
• $C_1$ = nombre de $1$-cycles indépendants sur la variété $V$.

Il est important de noter que les entiers $M_0$ et $M_1$ sont des caractéristiques de la fonction $f$, alors que les entiers $C_0$ et $C_1$ sont des caractéristiques topologiques de la variétés $V$ dont les définitions ne font nullement intervenir la fonction $f$.

Quelques mots sur la définition de l’entier $C_1$

Ce dernier nombre $C_1$ est défini de manière subtile. Pour les lecteurs savants (par exemple, ceux qui ont déjà lu notre rubrique homologie), il suffit de dire que c’est le premier nombre de Betti de $V$ modulo $2$, c’est-à-dire la dimension du premier groupe d’homologie de $V$ à coefficient dans $\mathbb{Z}/2\mathbb{Z}$. Les autres retiendront simplement l’idée vague que $C_1$ « compte le nombre maximum de courbes fermées simples indépendantes tracées sur $V$ ». Ici, on considère qu’un nombre fini de courbes fermées simples disjointes [17] tracées sur $V$ sont « indépendantes » si aucun sous-ensemble de ces courbes ne forme le bord d’une surface à bord contenue dans $V$. On peut montrer que, pour les variétés $V$ qui sont fermées, il n’y a jamais une infinité de cercles ayant cette propriété, et que par conséquence $C_1$ est bien un nombre entier naturel. Voici un exemple de famille maximale de cercles indépendants sur une surface fermée de l’espace usuel :

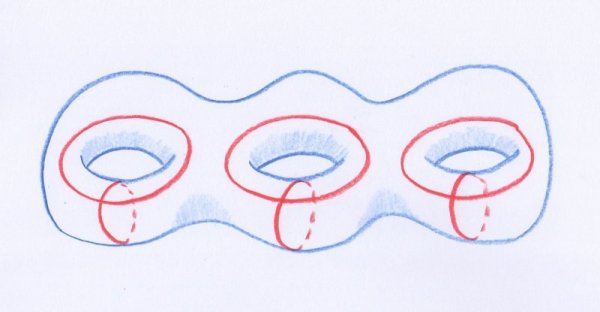
Une famille maximale de cercles indépendants sur une surface fermée. Dans ce cas, on a donc $C_1 = 6$.

Pouvez-vous deviner, en raisonnant par analogie, ce que valent les nombres $C_1$ pour les surfaces de la classification de Möbius ?

Birkhoff découvrit l’inégalité suivante, qui relie les nombres $M_0, M_1$ de minima et de points de mini-max de la fonction et les caractères topologiques $C_0, C_1$ de la variété sous-jacente :

Cette inégalité montre que, en toute dimension finie, plus il y a de minima, et plus il y a de points de mini-max (cols généralisés). Mais elle peut être vue aussi comme une manière de majorer le caractère topologique $C_1$ de la variété ambiante dès que l’on connaît les nombres de minima et de points de mini-max d’une fonction sur cette variété. C’est l’exemple le plus simple du fait que la connaissance d’informations sur une fonction définie sur une variété permet d’accéder à des informations topologiques sur cette variété.

La figure suivante, extraite d’un article [18] du mathématicien allemand William Threlfall de 1939, illustre cette inégalité pour une situation à la Möbius, avec une surface qui est un tore :

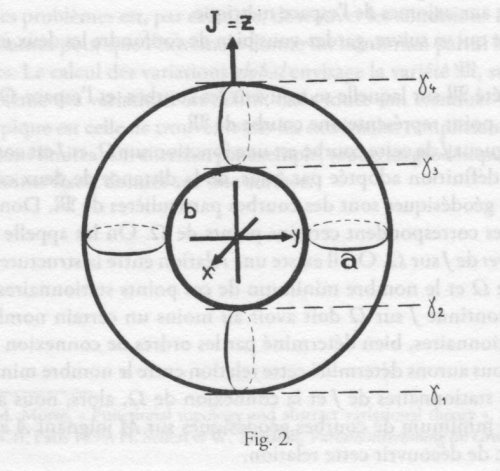
Une figure d’un article de Threlfall. On y voit un tore de révolution, et l’indication des quatre niveaux de la fonction hauteur qui donnent des niveaux singuliers par découpage. On a un sommet, deux cols et un fond.

Dans ce cas :

$$\begin{array}{c} M_0 = 1, M_1 = 2 , \\ C_0 = 1 , C_1 = 2 \end{array}$$

ce qui montre que l’inégalité est ici une égalité. Les cercles $a$ et $b$ de la figure sont un ensemble maximal de cercles indépendants, ce pourquoi $C_1=2$. Quant à l’égalité $C_0=1$, elle correspond au fait que le tore est connexe.

Les inégalités de Morse

Marston Morse, qui fit sa thèse avec Birkhoff, s’intéressait lui aussi aux problèmes d’existence de géodésiques. Il y pensait à la manière expliquée plus haut, comme à des problèmes d’existence de points singuliers pour des fonctions sur des variétés de dimension infinie. Pour cette raison, comme Birkhoff, il voulut mieux comprendre ce qui se passait dans des problèmes analogues sur les variétés de dimension finie quelconque. L’idée étant toujours que la variété de dimension infinie des chemins associée au problème considéré pouvait être vue comme une limite de variétés de dimension finie [19].

Morse généralisa l’inégalité de son maître dans un article [20] de 1925. Il montra que l’on avait en fait un système d’inégalités, chacune d’entre elles étant associée à un type de point singulier de la fonction hauteur.

Plus précisément, considérant une fonction $f$ lisse [21] « générale » [22] définie sur une variété $V$ de dimension $n$, il partagea en $n+1$ classes les points singuliers de $f$. Pour cela, il exprima la fonction $f$ à l’aide d’un système de coordonnées locales $(x_1, x_2, \dots, x_n)$ au voisinage d’un point singulier. En soustrayant la valeur prise en ce point, il se ramena au cas où la fonction s’y annule. Il montra que, dans le cas général, on pouvait toujours choisir les coordonnées locales $(x_1, x_2, \dots, x_n)$ de telle manière que, dans ces coordonnées, la fonction $f$ s’écrive sous la forme $\pm x_1^2 \pm x_2^2 \pm x_3^2 \pm \cdots \pm x_n^2$. C’est le « lemme de Morse », dont nous donnons une preuve ici. Il appela « indice » du point singulier le nombre de carrés apparaissant avec le signe « $-$ ». Par exemple :

• minimum = indice $0$ : $x_1^2 + x_2^2 + x_3^2 + \cdots + x_n^2$ ;
• mini-max = indice $1$ : $\mathbf{-} x_1^2 + x_2^2 + x_3^2 + \cdots + x_n^2 $ ;
• indice 2 : $\mathbf{-} x_1^2 \mathbf{-} x_2^2 + x_3^2 + \cdots + x_n^2$ ;
• indice 3 : $\mathbf{-} x_1^2 \mathbf{-} x_2^2 \mathbf{-} x_3^2 + \cdots + x_n^2$ ;
• ...
• maximum = indice $n$ : $- x_1^2 - x_2^2 - x_3^2 - \cdots - x_n^2$.

Cet indice peut s’interpréter plus intuitivement de la manière suivante : c’est le nombre maximum de directions de mouvement indépendantes passant par le point, qui permettent de diminuer la valeur de la fonction $f$. Ou bien, si on pense que la fonction représente l’altitude d’un relief, c’est le nombre maximum de directions indépendantes qui permettent de descendre du point considéré de ce relief.

Notons $M_k$ le nombre de points singuliers d’indice $k$ de la fonction $f$, et $C_k$ l’ordre de connexion de dimension $k$ de la variété $V$ [23]. Morse prouva les généralisations suivantes de l’inégalité du mini-max de Birkhoff pour une variété fermée de dimension $n$ :

Attention au fait que la dernière inégalité est bien toujours une égalité !

En additionnant chaque paire d’inégalités consécutives du système précédent, on déduit que :

$$M_k \geq C_k \mbox{ pour tout } k = 0, 1, ..., n.$$

Morse exprima ce fait en disant qu’il y a des points singuliers de la fonction $f$ qui sont « topologiquement nécessaires ». C’est-à-dire que la structure topologique de la variété $V$ impose l’existence d’un certain nombre de cols généralisés de chaque sorte, et cela indépendamment du choix de la fonction lisse $f$.

Un exemple

Voici un exemple dans lequel toutes les inégalités de Morse sont en fait des égalités. On considère deux courbes fermées lisses et sans auto-intersections, tracées dans le plan euclidien (tracées en couleur ocre, à gauche sur la figure di-dessous). On cherche des segments reliant ces courbes, qui soient perpendiculaires aux deux tangentes aux points de contact avec les courbes [24]. Ce problème peut se traduire en un problème de recherche de points singuliers d’une fonction sur une surface. Cette surface est l’ensemble des couples de points situés sur les deux courbes, c’est-à-dire leur produit cartésien. Il s’agit d’un tore (à droite sur la figure). La fonction que l’on considère sur ce tore est le carré de la distance entre ces deux points. On montre alors que les points singuliers de cette fonction correspondent exactement à la situation géométrique considérée.

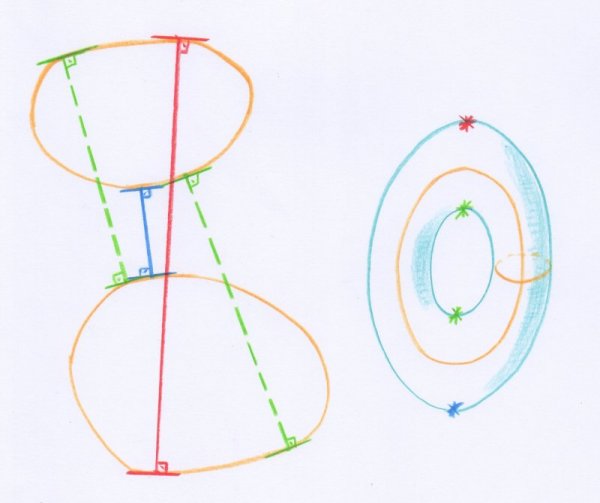
Les quatre segments perpendiculaires aux deux courbes. Le plus long correspond à un maximum de la fonction longueur, le plus court à un minimum, et les deux restants correspondent à des cols sur le tore associé. En traits interrompus sont représentés les segments qui correspondent aux cols.

Pour les courbes du dessin précédent on a :

$$\begin{array}{c} M_0 = C_0= 1, M_1 = C_1= 2 , M_2 = C_2 =1. \end{array}$$

Voici maintenant un exemple de courbes pour lesquelles, dans le même problème, toutes les inégalités de Morse sont strictes :

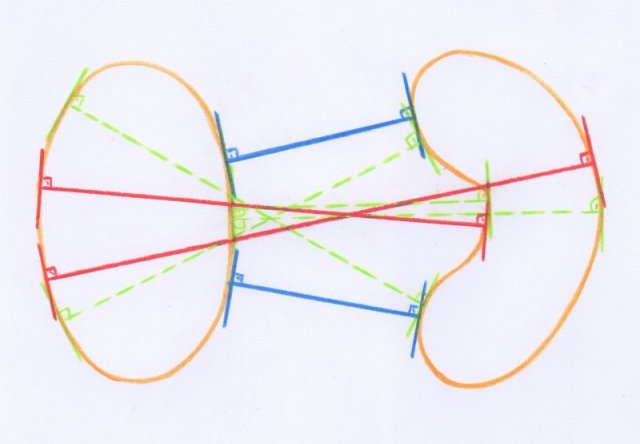
Dans cette situation on a deux fonds, quatre cols et deux sommets sur le tore des paires de points des deux cercles. En traits interrompus sont représentés les segments qui correspondent aux cols.

Dans cette situation, on a :

$$\begin{array}{c} M_0 = 2, M_1 = 4 , M_2 =2 ; \\ C_0 = 1 , C_1 = 2, C_2=1. \end{array}$$

Nous avons choisi d’illustrer les inégalités de Morse par ce problème concernant des couples de courbes fermées planes, afin de mettre en évidence une situation qui mène à considérer des variétés de dimension arbitrairement grandes. Le problème de départ concerne bien des objets vivant dans le plan euclidien. Mais il concerne l’existence de plusieurs points, ayant dans leur ensemble une propriété spéciale. Chacun de ces points peut varier de manière indépendante sur une courbe. Eh bien, on peut penser à ce multiplet de points comme à la donnée d’un seul point, qui varie lui dans le produit cartésien des courbes données. S’il y a $n$ points, alors ce produit cartésien est de dimension $n$. Et si chacune de ces courbes est homéomorphe à un cercle, alors ce produit cartésien est homéomorphe à un « tore » généralisé, de dimension $n$... Ce sont aussi des exemples de ce type qui ont mené les mathématiciens à développer des manières de penser les phénomènes géométriques ou topologiques en dimension finie quelconque.

La démonstration de Morse de ses inégalités était compliquée, et difficilement communicable en termes géométriques simples. Cela restait un défi pour les géomètres d’en proposer de plus intuitives. Nous verrons plus bas une élégante manière d’y penser « à la Cayley », proposée par Thom. Pour une preuve plus formelle, nous renvoyons les lecteurs à cet article.

Revenons aux géodésiques. Morse appliqua sa théorie du lien entre structure topologique de l’espace et nombres de points singuliers de divers types des fonctions définies sur cet espace, afin de prouver le théorème suivant, dans un article [25] de 1929 :

Qu’est-ce qu’une « sphère de dimension arbitraire » ? Il y a tout d’abord les sphères « rondes », généralisations des sphères usuelles de l’espace euclidien tridimensionnel. Ce sont les lieux des points de l’espace cartésien $\mathbb{R}^n$ situés à égale distance d’un point fixe de cet espace, le centre de la sphère. Par exemple, la sphère de rayon $1$ centrée à l’origine est le lieu des points de coordonnées $(x_1, ..., x_n)$ vérifiant l’équation :

$$ x_1 ^2 + x_2^2 + \cdots + x_n^2 = 1.$$

Maintenant, en toutes dimensions une telle sphère ronde peut être cabossée, allongée, tordue, gondolée ... mais sans la déchirer ou la plier. On obtient une sous-variété lisse de $\mathbb{R}^n$, homéomorphe à une sphère ronde, sur laquelle on peut mesurer les longueurs des courbes à l’aide de la distance entre les points de l’espace ambiant $\mathbb{R}^n$. Il s’agit de l’une des « sphères » auxquelles s’applique le théorème précédent de Morse.

Voici par exemple plusieurs géodésiques reliant deux points, sur une sphère tordue de l’espace usuel :

Trois exemples de géodésiques reliant deux points donnés sur une surface sphérique de l’espace usuel.

La théorie développée par Morse pour relier la forme topologique d’un espace aux divers points critiques d’une fonction vivant dessus impressionna tellement ses contemporains, et elle eut des applications si importantes, que l’on parle depuis de « théorie de Morse ». Pourtant, il ne s’agit pas d’une théorie figée. Elle a continué à évoluer, et à s’enrichir de métamorphoses et d’applications. Avant de conclure, je désire en mentionner deux [27].

Le point de vue de Thom

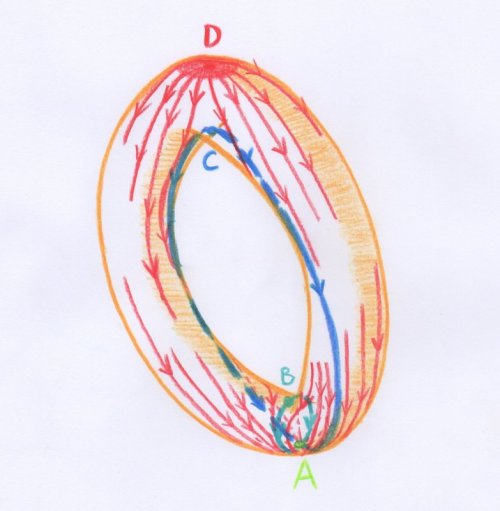
En 1949, dans son premier article [28], le mathématicien français René Thom proposa un principe de démonstration très intuitif des inégalités de Morse pour une fonction lisse sur une variété fermée de dimension quelconque. Ce principe reprenait les idées de base de Cayley, en imaginant ce qui se passe avec un liquide qui s’écoule sur le paysage décrit par la fonction donnée [29].

Plus précisément, en supposant que la fonction n’a que des points singuliers généraux, Thom montra que pour chaque point singulier, l’union du point et des lignes d’écoulement de Cayley qui semblent provenir de ce point est une « cellule » homéomorphe à un espace cartésien $\mathbb{R}^k$ dont la dimension $k$ est égale à l’indice du point singulier. On obtient ainsi une décomposition de la variété en cellules deux à deux disjointes [30].

Voici par exemple quel est l’aspect qualitatif de cette décomposition lorsque l’on penche un peu le tore de la figure de Threlfall, afin que la ligne d’écoulement qui part du col supérieur aboutisse au point le plus bas du tore, et non pas au col inférieur :

L’écoulement de l’eau sur un tore incliné.

Ici la fonction sur le tore est simplement la fonction hauteur au-dessus d’un plan horizontal. Les points singuliers sont notés $A, B, C, D$. Le point $A$ est un minimum — il est donc d’indice $0$ —, les points $B$ et $C$ sont des cols — ils sont donc d’indice $1$ — et le point $D$ est un maximum — il est par conséquent d’indice $2$.

• Le point $A$ étant le plus bas possible, le liquide ne peut pas s’en écouler, donc la cellule associée est réduite à ce point.
• La cellule associée au col $B$ est formée du point $B$ et des deux lignes d’écoulement qui semblent surgir de $B$. Elle est donc de dimension un. Elle aboutit au point $A$, que l’on ne considère pas comme faisant partie de cette cellule.
• De même pour le col $C$.
• La cellule associée au maximum $D$ est formée du point $D$ et des lignes de plus grande pente qui semblent partir de $D$. On peut imaginer que la petite calotte que j’ai représentée au sommet du dessin est remplie de liquide, qu’on laisse ensuite couler sur le tore. Cette cellule est de dimension deux.

Par ailleurs, Poincaré avait expliqué qu’une décomposition en cellules d’une variété permet de calculer ses nombres de connexion $C_0, C_1, ..., C_n$ [31]. Thom constata que la décomposition en cellules qu’il décrit ayant précisément $M_k$ cellules de dimension $k$, et cela pour tout $k$, on peut en déduire directement les inégalités de Morse « faibles » $M_k \geq C_k$ [32].

Thom n’entra pas dans les détails, mais on peut en effet tout faire marcher comme il l’a décrit. Cela est techniquement compliqué, mais la vision qu’il a esquissée a inspiré bon nombre de mathématiciens.

Le point de vue de Smale

L’un de ceux qui ont le plus été inspirés par la décomposition en cellules imaginée par Thom a été le mathématicien américain Stephen Smale. Mais avant de parler de cela, revenons à Poincaré. Dans le Cinquième complément à l’Analysis Situs, ce dernier énonça l’une des plus fameuses conjectures du XXe siècle, que l’on peut formuler ainsi :

Cette conjecture ne fut démontrée qu’en 2003, par le mathématicien russe Grigori Perelman.

Ce qui est curieux, est que l’analogue de la conjecture de Poincaré formulé en dimension au moins $5$ résista beaucoup moins longtemps. Plus précisément, en 1960 Smale démontra que [34] :

Smale prouva ce théorème en généralisant à toutes les variétés de dimension finie les décompositions en anses utilisées par Heegaard pour décrire la structure des variétés de dimension $3$. Plus précisément, il partit d’une fonction lisse n’ayant que des points singuliers généraux. Il montra qu’à chaque point singulier est associé un certain type d’anse, obtenue en épaississant la cellule de Thom qui lui correspond, et que la variété est recouverte par les anses correspondant à tous les points critiques. Il élabora ensuite un analogue du calcul de Möbius, en permettant aux anses de glisser les unes sur les autres et de fusionner.

Voici un exemple de telle fusion, dans le cas des surfaces :

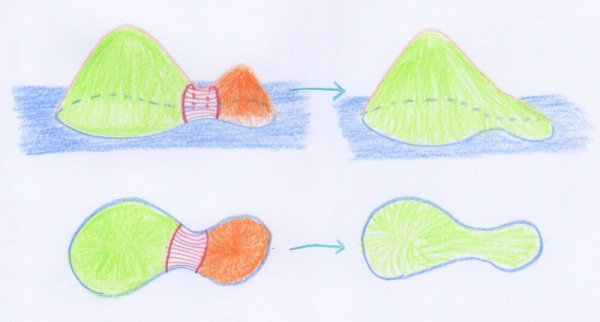
Une fusion de deux disques (anses d’indice $0$) et d’une anse au sens usuel (anse d’indice $1$) aboutit à un seul disque.

A priori, dans cet exemple on ne voit qu’une seule anse, correspondant au col entre les deux collines. En fait, Smale considéra aussi les deux disques entourant les sommets comme des « anses », afin d’avoir bien une anse par point singulier. La figure précédente indique donc la fusion de trois anses en une seule.

Smale montra que, sous les hypothèses du théorème précédent, on peut se ramener par glissements, fusions et anti-fusions [35] successifs à juste deux anses d’indice $0$, qui sont des boules recollées le long de leur bord. Il est alors simple d’en déduire la conclusion du théorème [36].

Smale utilisa les décompositions en anses pour obtenir bien d’autres théorèmes sur les variétés de dimension au moins $5$ [37]. Ce qui est curieux est que, même si on a de telles décompositions en toutes dimensions, la manière de les utiliser en dimensions $3$ et $4$ est radicalement différente de celle en dimensions supérieures à $4$. Mais cela est une autre histoire...

Conclusion

Les travaux de Morse ont appris aux géomètres du XXe siècle que l’on peut étudier la structure globale d’une variété en choisissant une fonction lisse définie sur cette variété, et en considérant cette situation comme une généralisation de celle qui conduit à la construction d’une carte topographique. La théorie de Morse révèle des liens profonds et subtils entre la topologie de la variété et le comportement de la fonction au voisinage de ses points singuliers. La diversité des applications est étonnante, allant de la recherche de géodésiques fermées à la caractérisation topologique des sphères de grande dimension.

Après ce survol à haute altitude de plus de cent ans de mathématiques, il est temps d’inviter nos lecteurs à redescendre plus près du niveau de la mer puis à plonger dans la technique, en continuant la lecture de la rubrique que nous consacrons à la théorie de Morse. Pour les motiver et les mettre en garde tout à la fois, nous leur livrons l’aphorisme suivant, titre d’un article du mathématicien hongrois-américain Raoul Bott [38] :

La théorie de Morse est indomptable.