|
> Contexte historique > Les discussions entre Riemann et Betti sur l’Analysis Situs Les discussions entre Riemann et Betti sur l’Analysis Situs |
Enrico Betti discuta avec Riemann de l’extension de la notion d’ordre de connexion du cas des surfaces (voir notre analyse du manuscrit posthume de Riemann [1]) aux dimensions supérieures. Deux lettres adressées par Betti à son ami Tardy, datées du 6 et du 16 Octobre 1863 (traduites en Anglais par Weil dans [2]), permettent de nous faire une idée du contenu de ces discussions.
Ces lettres traitent principalement des espaces (« spazii ») de dimension $3$, le cas des dimensions arbitraires étant abordé rapidement à la fin de chacune d’entre elles. Les notions et les constructions décrites sont illustrées grâce aux exemples suivants :
- « l’espace compris entre deux sphères concentriques » (le produit d’une sphère bidimensionnelle et d’un segment) ;
- « l’espace contenu à l’intérieur d’un anneau plein » (un tore plein, produit d’un disque et d’un cercle) ;
- « l’espace compris dans un anneau creux » (un tore épais, produit d’un tore bidimensionnel et d’un segment ;
- « une sphère avec une cavité annulaire à l’intérieur » (le complémentaire, dans une boule fermée de dimension $3$, de l’intérieur d’un tore plein non noué).
Voici les parties de la lettre du 6 Octobre 1863 qui ne concernent pas les exemples (c’est nous qui mettons en évidence les termes-clef) :
« J’ai à nouveau parlé avec Riemann de la connexion des espaces, et je m’en suis fait une idée exacte.Un espace est appelé simplement connexe quand chaque surface fermée, contenue dans celui-ci, en limite à elle seule complètement une partie, et chaque ligne fermée contenue en même temps dedans limite complètement une surface contenue entièrement dans cet espace [...].
L’ordre de connexion est donc représenté par deux nombres ; notons-le par $(m,n)$ quand on a $m$ sections superficielles et $n$ sections linéaires qui le rendent simplement connexe. [...] La généralisation à un plus grand nombre de dimensions est facile ; et l’importance, pour les intégrales multiples, de toute cette théorie est évidente. Riemann est parvenu à la notion de section à partir d’une définition que lui a donnée Gauss lors d’une conversation privée, sur un autre sujet. Dans ses écrits [de Gauss] on trouve affirmé que l’analyse du site [« l’analisi di sito »], c’est-à-dire ces considérations sur les quantités indépendamment de leurs mesures, est « wichtig » [importante], et pendant les dernières années de sa vie il s’est beaucoup occupé d’un problème d’analyse de situation [« analisi di situazione »] : étant donné un fil qui s’enroule plusieurs fois, et en connaissant, aux points où il s’intersecte, la partie qui reste au-dessus et celle qui reste en-dessous, déterminer si on peut le défaire sans faire des nœuds ; problème qu’il n’a pas réussi à résoudre, sauf dans des cas particuliers ... »
La notion de « simple connexité » est bien celle mentionnée par Riemann dans son manuscrit posthume. Par contre, l’ordre de connexion n’est pas mesuré de la même manière : chez Riemann, on comptait les sous-variété sans bord indépendantes homologiquement (modulo $2$), ici on compte des sections transverses simplement connexes. Nous avons indiqué dans le commentaire du texte de Riemann que celui-ci n’avait pas proposé une telle définition, ses notes ne contenant qu’une première esquisse de l’étude des variétés de dimension supérieure à l’aide du découpage le long d’une suite de sections transverses. En particulier, nous avons remarqué que Riemann n’imposait aucune restriction à ces sections transverses, à part le fait de ne pas disconnecter, et de faire passer de la classe $(a_k)$ à la classe $(a_{k-1})$.
Ces lettres de Betti indiquent une évolution par rapport à la pensée décrite dans les notes de Riemann, puisqu’il s’agit à présent de découper uniquement le long de sections « simplement connexes ». Le texte de Riemann est donc probablement antérieur à ces lettres, ce que nous ne pouvons savoir à coup sûr, car il est non daté.
Remarquons aussi le fragment « l’importance, pour les intégrales multiples, de toute cette théorie est évidente » de la lettre précédente, qui montre que pour Riemann, ces considérations sur les ordres de connexion étaient intimement liées à la théorie des intégrales multiples. Ce lien ne sera complètement explicité qu’avec le théorème de de Rham (voir aussi notre Commentaire du §7 de l’Analysis Situs). Il s’agira en fait d’un lien entre l’homologie réelle et non pas modulo $2$ et les intégrales multiples.
Nous apprenons aussi dans cette lettre qu’à la fin de sa vie Gauss s’intéressait au problème de déterminer à partir d’un diagramme de nœud s’il s’agissait d’un nœud trivial ou pas, ce qui est bien un problème topologique. Le lecteur désireux d’apprendre quels problèmes menèrent Gauss à l’étude des nœuds et des entrelacs pourra consulter les articles [3] et [4] de Moritz Epple.
Venons-en à présent à la lettre de Betti datée du 16 Octobre 1863, en omettant à nouveau les exemples :
« Riemann démontre, avec beaucoup de facilité, que l’on peut réduire un espace quelconque à être simplement connexe, à l’aide de sections linéaires et de sections superficielles simplement connexes.Un espace connexe ne change pas d’ordre de connexion si on restreint ou augmente les surfaces qui le limitent, en faisant bouger leurs points vers l’intérieur de l’espace, et que l’espace en vient ainsi à perdre une ou plusieurs dimensions, pourvu que ces mouvements se fassent avec continuité et sans ruptures. Afin qu’un espace soit simplement connexe, il est nécessaire qu’il puisse ainsi être réduit à un seul point. [...] »
Cette dernière phrase est erronée. En effet, une rétraction par déformation ne change pas le type d’homotopie. Donc, si on se ramène à un point, c’est que l’on était parti d’un espace qui avait en particulier l’homologie d’un point. Mais la « simple connexité » selon Riemann et Betti signifie que c’est seulement l’homologie modulo $2$ qui est celle d’un point ...
En fait, même si une variété (à bord) de dimension $3$ est homéomorphe à une boule, il se peut que le procédé décrit par Betti la ramène à un complexe cellulaire bidimensionnel sans arêtes libres, donc pour lequel le processus est bloqué, comme le montre un exemple célèbre, la « maison de Bing » (voir le bloc suivant). Même dans ce cas, il n’est donc pas vrai que, pour qu’une variété à bord de dimension $3$ soit homéomorphe à une boule, il est nécessaire qu’elle se ramène à un point par une rétraction par déformation.
La maison de Bing
Dans [5], Bing décrivit un complexe polyédral de dimension $2$ plongé dans l’espace euclidien tridimensionnel, qui s’obtient en rétractant par déformation une boule, mais qui ne peut pas être réduit plus, car il lui manque des arêtes libres (en termes modernes, on dit qu’il ne peut pas s’effondrer).
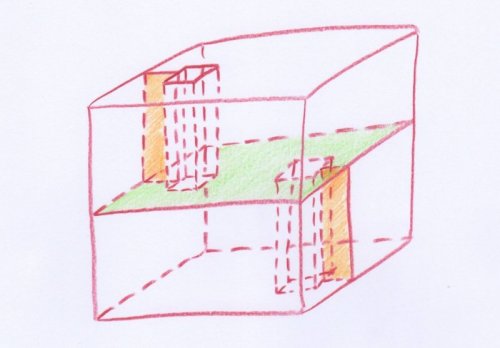
Décrivons ce complexe par rajouts et éliminations successifs de surfaces, en partant de la surface $C_0$ d’un cube plein $Q$ :
- Soit $C_1$ l’union de $C_0$ et d’un carré médian $M$, obtenu en intersectant l’intérieur de $C_0$ avec un plan équidistant de deux faces opposées. On imagine que $C_1$ est une maison ayant deux étages, avec une pièce à chaque étage.
- On rajoute dans chaque pièce une colonne prismatique droite creuse, de base carrée, ces colonnes étant situées près de murs opposés et les bases au niveau de la paroi médiane $M$ étant disjointes. Soit $C_2$ le résultat de ce rajout.
- On enlève les intérieurs des bases des deux colonnes, en obtenant le complexe cellulaire $C_3$.
- On rajoute deux parois rectangulaires, du sol au plafond, allant de chaque colonne au mur le plus proche, qui ont comme but d’empêcher de tourner autour de chaque colonne. On obtient ainsi le complexe $C_4$.
Ce processus est illustré dans la figure suivante. Les parois rectangulaires rajoutées en dernier y sont représentées en orange, et ce qui reste du carré médian en vert.
La maison de Bing est le complexe $C_4$. On peut se convaincre que $C_4$ s’obtient par une rétraction par déformation à partir du cube plein $Q$, en creusant à partir des bases des colonnes situées sur les faces du cube, d’abord à l’intérieur des colonnes, puis à l’intérieur de la pièce à laquelle on parvient de cette manière.
Betti explique ensuite, sur les exemples mentionnés au début de ce commentaire, une stratégie pour trouver des sections transverses le long desquelles découper, non seulement « simplement connexes », mais même homéomorphes à des boules : en termes modernes, il s’agit de rétracter par déformation une variété à bord sur un « espace » de dimension plus petite. En général, cet autre espace n’a plus de bord que l’on puisse rétracter par déformation. Pour cette raison, on le perce à plusieurs endroits où il est, localement, une variété. On fait apparaître ainsi de nouvelles composantes de bord, et l’on itère le procédé.
Voici comment Betti décrit cette méthode dans son dernier exemple, le plus compliqué :
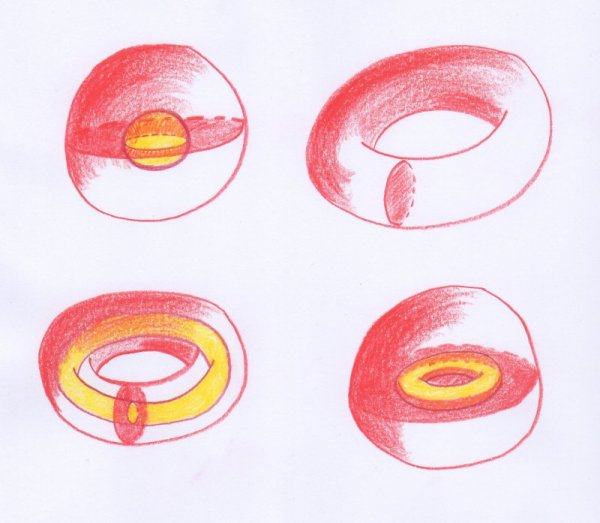
« Une sphère avec une cavité annulaire à l’intérieur, si tu contractes la surface sphérique elle perd une dimension et se réduit à une surface plane qui joint les bords intérieurs de la surface annulaire. Avec un point de section on réduit cette surface à une ligne circulaire dont le centre se trouve sur l’axe interne de l’anneau, et à une surface circulaire plane qui a le même centre que l’anneau. Avec un autre point de section la ligne circulaire se réduit à un point du bord de la surface circulaire plane, qui sans aucune autre section peut être réduite à un point. Donc une sphère avec une cavité annulaire se rend simplement connexe à l’aide d’une section linéaire et d’une section superficielle simplement connexe. Son ordre de connexion est $(1,1)$. »
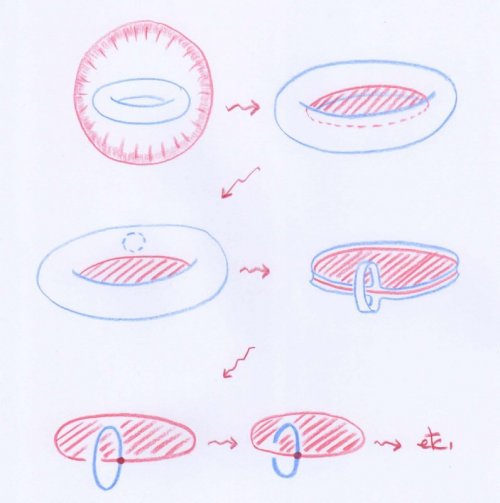
Afin de visualiser ses explications, imaginons que la cavité annulaire est l’intérieur d’un tore de révolution $T$, contenu à son tour à l’intérieur d’une sphère $S$, ayant l’axe de révolution du tore comme axe de symétrie. La variété $M$ de dimension $3$ dont il s’agit est la région comprise entre $T$ et $S$. Elle peut se rétracter par déformation sur l’union $\Sigma$ de $T$ et du disque $D$ perpendiculaire à l’axe de symétrie, centré dessus et n’intersectant $T$ que le long de son bord. Si on perce $\Sigma$ en enlevant un petit disque (topologique) de $T$ qui ne rencontre pas $D$, le résultat de ce percement se rétracte par déformation sur l’union de $D$ et d’un cercle méridien de $T$. On perce ensuite ce cercle. Le résultat se rétracte par déformation sur $D$, qui se rétracte ensuite sur son centre.
Ce processus est illustré sur la figure suivante :
Reprenons la lettre, et venons-en aux deux paragraphes finaux, qui concernent la généralisation aux dimensions arbitraires :
« En généralisant, on voit qu’une variété à $n$ dimensions peut toujours, à l’aide de diminutions continues et sans ruptures, être réduite à la dimension $n-1$. À l’aide de points de sections on pourra la réduire à $n-2$ dimensions, à l’aide d’autres points de section à la dimension $n-3$ ; et ainsi de suite, jusqu’à ce qu’on la réduise à un point. Aux premiers points de section correspondent des sections linéaires ; aux seconds des sections superficielles simplement connexes ; aux troisièmes, des sections de troisième dimension simplement connexes, ... ; aux derniers, des sections de dimension $n-1$ simplement connexes.Le nombre de sections linéaires est égal au nombre des modules de périodicité d’une intégrale $(n-1)$-uple ; le nombre des sections superficielles simplement connexes au nombre de modules de périodicité d’une intégrale $(n-2)$-uple ... ; le nombre des sections de dimension $(n-1)$ simplement connexes, au nombre de modules de périodicité d’une intégrale simple, toutes ces intégrales étant prises dans l’espace considéré. Donc, comme les nombres de modules de périodicité sont bien déterminés, le seront toujours aussi les nombres de différentes sections qui rendent l’espace simplement connexe, indépendamment de la manière de les pratiquer ... »
Ici Betti est plus précis que dans sa première lettre sur le lien entre les ordres de connexion définis en comptant des sections transverses simplement connexes et la théorie des intégrales multiples sur l’« espace » considéré. Hélas ce qu’il affirme est faux : en effet, le nombre des modules de périodicié en dimension $k$ est égal au rang du groupe d’homologie réel en dimension $k$, qui peut être nul même en présence de sections transverses de dimension $n-k$. Néanmoins, ce paragraphe est intéressant pour les raisons suivantes :
- on peut y voir l’affirmation de l’espoir que la situation en dimension arbitraire ne soit pas plus compliquée que pour les surfaces.
- on peut aussi y voir le problème qui mena à la découverte du phénomène de dualité de Poincaré. En effet, il est question de compter le nombre de périodes indépendantes en dimension $k$, à l’aide de sections transverses de dimension complémentaire $n-k$. Si l’on est parti d’une variété close, en créant un bord par l’enlèvement d’une boule, les sections transverses se complètent en des cycles de la variété initiale en rajoutant dans la boule les cônes sur leurs bords. On est ramenés à se dire que les nombres de cycles en dimensions complémentaires sont les mêmes, tout le problème étant de savoir comment les compter pour que ceci soit vrai ...
Betti développa les idées contenues dans ces lettres dans son article [6] paru en 1871. Les notions de base y sont définies, hélas, de manière très imprécise de notre point de vue. Par exemple, voici comment il introduit la notion de variété :
« Soient $z_1, z_2, ..., z_n$ $n$ variables qui peuvent prendre toutes les valeurs réelles de $- \infty$ à $+ \infty$. Le champ $n$ fois infini des systèmes de valeurs de ces variables, nous l’appellerons un espace de $n$ dimensions et nous le noterons $S_n$. Un système $(z_1^0, z_2^0, ..., z_n^0)$ déterminera un point $L_0$ de cet espace, et $(z_1^0, z_2^0, ..., z_n^0)$ seront appelés les coordonnées de ce point.Un système de $m$ équations déterminera un champ du système de valeurs de $n-m$ variables indépendantes qui sera un espace $S_{n-m}$ de ce nombre de dimensions, contenu dans $S_n$. »
Le premier paragraphe, trivial pour nous, montre que l’on en était aux débuts de la pensée en termes géométriques sur les questions concernant les ensembles de solutions de systèmes d’équations à un nombre arbitraire de variables. Mais de quel type d’équations s’agit-il ? Quelles conditions doit-on imposer pour être sûrs d’obtenir un « espace » de dimension adéquate ? Betti n’aborde pas ces questions.
Une partie de l’article développe des formules de calcul intégral grâce auxquelles Betti tente de montrer l’égalité des nombres de « modules de périodicité » et de sections transverses, en dimension $1$ et en codimension $1$. On n’y trouve rien qui concerne cette égalité pour les dimensions intermédiaires. On trouve peut-être là l’explication de l’intervalle assez important entre les conversations avec Riemann et la publication de l’article : Betti aurait cherché, sans succès, une telle preuve.
Les deux lettres à Tardy montrent bien que le squelette de l’article de Betti provient de ces discussions avec Riemann. Betti a le mérite de s’être intéressé à ces recherches de Riemann à une époque où bien peu de monde le faisait, d’avoir énoncé publiquement le problème de la mesure de la connexion des espaces de dimension arbitraire à l’aide de sections transverses adéquates, ainsi que celui du lien avec la théorie de l’intégration, et enfin d’avoir proposé une première approche de ces problèmes, en suivant les idées de Riemann.
Les lecteurs pourront trouver d’autres détails sur les deux lettres de Betti à Tardy dans le Chapitre II.3 du livre [7] de Pont.
[1] Bernhard Riemann, Fragment aus der analysis situs. Dans Gesammelte Mathematische Abhandlungen, Teubner, Leipzig, 1892. Publication posthume de notes écrites à une date indéterminée. Traduction : Fragment sur l’Analysis Situs. Dans Œuvres mathématiques, Gauthier Villars, Paris, 1898. Traduction par L. Laugel. Réimpression Gabay, Sceaux, 1990, 414-419, 448-451.
[2] André Weil, Riemann, Betti and the birth of topology, Arch. Hist. Exact Sci. 20 (1979), no. 2, 91-96.
[3] Moritz Epple, Orbits of asteroids, a braid, and the first link invariant, Math. Intelligencer 20 (1998), no. 1, 45-52.
[4] Moritz Epple, Geometric aspects in the development of knot theory. Dans History of topology, North-Holland, Amsterdam, 1999, pp. 301-357.
[5] R. H. Bing, Some aspects of the topology of 3-manifolds related to the Poincaré conjecture. Dans Lectures on modern mathematics, Vol. II, Wiley, New York, 1964, 93-128.
[6] Enrico Betti, Sopra gli spazi di un numero qualunque di dimensioni, Annali di Mat. Pura ed Applicata (2) 4 (1871), 140-158.
[7] Jean-Claude Pont, La topologie algébrique des origines à Poincaré, Presses Universitaires de France, Paris, 1974.