Approches de l’homologie chez Poincaré

Ce chapitre est basé sur l’article « La dualité de Poincaré » publié par Patrick Popescu-Pampu sur le site Images des Mathématiques.

À partir de 1895, Henri Poincaré développa une nouvelle forme de calcul, portant sur les « figures » vivant dans les espaces de dimension quelconque : le calcul des homologies. Elle lui permit de définir des mesures numériques de la forme d’un tel espace, leurs nombres de Betti.

Lorsque l’espace est refermé sur lui-même comme une surface sphérique, ces nombres vérifient une étonnante propriété de symétrie, qui porte depuis le nom de dualité de Poincaré. Poincaré en proposa deux stratégies de preuve. Nous décrirons ces stratégies, ainsi que les nouvelles mesures de la forme des espaces découvertes par Poincaré lorsqu’il méditait sur la deuxième d’entre elles : les invariants de torsion. Nous examinerons enfin quelques travaux précurseurs, afin de mieux mettre en évidence l’apport de Poincaré.

Poincaré et l’étude qualitative des espaces de dimension quelconque

Voici comment Poincaré présenta dans l’introduction de son article « Analysis Situs » de 1895 l’importance d’étudier les figures vivant dans des espaces de dimension quelconque qualitativement, « sans aucune considération de grandeur » ou, comme nous disons aujourd’hui, d’un point de vue topologique :

La Géométrie à $n$ dimensions a un objet réel ; personne n’en doute
aujourd’hui. Les êtres de l’hyperespace sont susceptibles de définitions
précises comme ceux de l’espace ordinaire, et si nous ne pouvons nous les
représenter, nous pouvons les concevoir et les étudier. [...]

L’emploi des figures a donc avant tout pour but de nous faire connaître
certaines relations entre les objets de nos études, et ces relations sont celles
dont s’occupe une branche de la Géométrie que l’on a appelée
Analysis situs, et qui décrit la situation relative des points, des lignes
et des surfaces, sans aucune considération de grandeur.

Il y a des relations de même nature entre les êtres de l’hyperespace ; il y a donc une Analysis situs à plus de trois dimensions, comme l’ont montré Riemann et Betti.

Parmi les divers espaces dont on peut étudier les propriétés topologiques, Poincaré décida de se concentrer sur les « variétés » (un terme qui fait probablement référence au fait que ses points représentent des lieux de variation de certains paramètres), qui sont simplement les analogues de dimension quelconque des courbes et des surfaces lisses de l’espace tridimensionnel. Mais, pour les besoins de ses démonstrations, Poincaré est obligé d’élargir progressivement son concept, ce qu’il fait sans le dire, juste en employant petit à petit le terme de variété pour des objets qui n’en sont pas selon la définition initiale. Nous attirerons à chaque fois l’attention sur ces moments de changement d’interprétation.

L’un des théorèmes essentiels de Poincaré dans ce domaine affirme en gros que tout espace refermé sur lui-même tel un cercle ou une sphère admet une symétrie interne : il y a le même nombre de sous-variétés indépendantes de chaque dimension que de la dimension complémentaire. Par exemple, dans une variété de dimension trois il y a autant de courbes indépendantes (sous-variétés de dimension $1$) que de surfaces indépendantes (sous-variétés de dimension $2$). La complémentarité des dimensions revient simplement à dire que $1 + 2 =3$.

Ce théorème, ainsi que ses réélaborations, portent le nom de théorèmes de dualité de Poincaré, le terme de dualité renvoyant à l’idée d’une symétrie entre deux sortes d’objets. On examinera l’évolution de la pensée de Poincaré à ce sujet, ainsi que certains des travaux de ses prédécesseurs qui se trouvent à l’arrière-plan de son travail.

Nous illustrerons les constructions clé à l’aide de courbes tracées sur des surfaces. Mais le théorème de dualité tel que l’énonce Poincaré ne devient non-trivial qu’à partir des variétés de dimension trois. Pour cette raison, le lecteur devra faire un effort d’imagination afin de comprendre comment ce qui est illustré sur des surfaces peut en fait être étendu en dimension quelconque. C’est justement l’une des contributions essentielles de Poincaré, d’avoir dégagé ainsi des constructions et des concepts géométriques valables en toute dimension.

Les frontières complètes

C’est dans son article « Analysis Situs » que Poincaré amorça l’élaboration de nouveaux types de calculs afin de décrire la forme des variétés de dimension quelconque : des calculs portant sur certaines figures de la variété donnée. C’est pour cette raison que l’on y voit l’article fondateur de la topologie algébrique : la topologie fournit les objets, et ceux-ci seront étudiés par le calcul algébrique.

Les figures considérées par Poincaré sont au début les sous-variétés de diverses dimensions de la variété donnée. Il sera bon de penser d’abord au cas des courbes fermées tracées sur une surface. Lorsqu’on découpe la surface le long d’une telle courbe, il se peut que l’on sépare la surface en deux morceaux, comme dans la partie gauche du dessin suivant, ou bien qu’on ne la sépare pas, comme dans la partie droite.

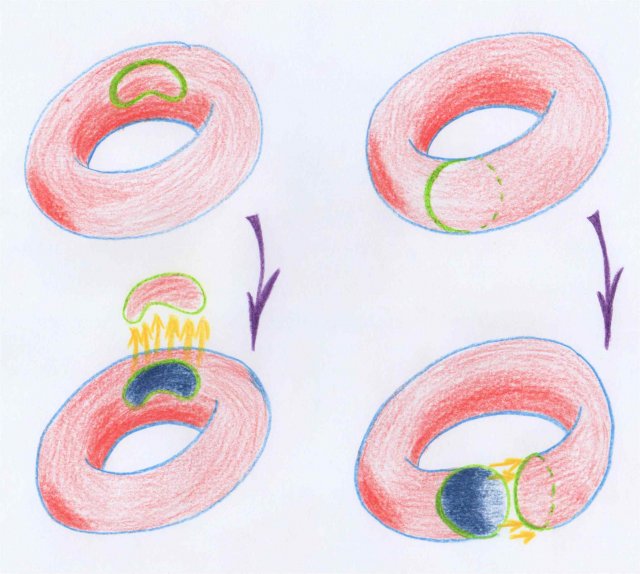
Dans le premier cas, la courbe est la frontière [1] d’une partie de la surface initiale, dans le deuxième cas elle ne l’est pas. C’est ce fait, d’être ou non la frontière d’une sous-variété que Poincaré a mis à la base de son calcul de la forme des espaces :

Considérons une variété $V$ à $p$ dimensions ; soit maintenant $W$ une variété à $q$ dimensions ($q \leq p$) faisant partie de $V$. Supposons que la frontière complète de $W$ se compose de $\lambda$ variétés continues à $q-1$ dimensions.

Nous exprimerons ce fait par la notation

$$v_1+v_2+\dots+v_\lambda\sim 0.$$

Par exemple, dans le dessin suivant sont représentées quatre sous-variétés (des cercles) d’une surface. Leur union est la frontière complète à la fois de la portion orange et de la portion violette de la surface. Avec la convention de Poincaré, cela s’écrit bien $v_1 + v_2 + v_3 + v_4 \sim 0$.

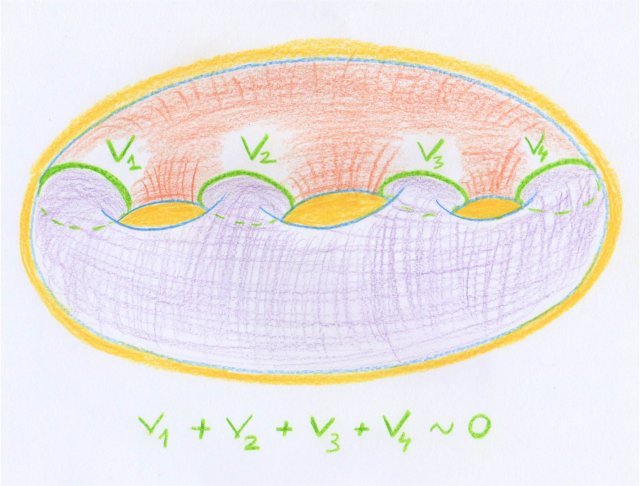
On voit que si l’on oublie certains des cercles, ceux qui restent ne forment plus la frontière complète d’une portion de la surface. Mais il est très important dans ce calcul de bien considérer les frontières complètes.

Remarquons qu’il s’agit de penser à la frontière non pas comme une union, mais comme une somme. Et ce, afin précisément d’enclencher un calcul, dans lequel un objet $A$ rajouté à lui-même ne donne pas de nouveau $A$, comme pour l’opération d’union ($A \cup A = A$), mais $2A$, comme dans les sommes de l’arithmétique et de l’algèbre ($A + A = 2 A$).

Puisqu’il est question de frontières, introduisons un terme de plus : une variété est dite fermée si, comme les surfaces avant découpage dans les figures précédentes, elle est refermée sur elle-même, sans frontière (de nos jours on dit qu’elle est compacte et sans bord).

Et la topologie devint algébrique !

C’est ici que la topologie devint partiellement algébrique, c’est-à-dire accessible aux calculs. La relation de la citation précédente doit en effet être pensée, selon Poincaré, en analogie avec les équations de l’algèbre usuelle :

Plus généralement la notation $k_1v_1 + k_2v_2 \sim k_3v_3 + k_4v_4$ où les $k$ sont des entiers et les $v$ des variétés à $q -1$ dimensions, signifiera qu’il existe une variété $W$ à $q$ dimensions faisant partie de $V$ et dont la frontière complète se composera de $k_1$ variétés peu différentes de $v_1$, [...], de $k_3$ variétés peu différentes de la variété opposée à $v_3$ [...]. Les relations de cette forme pourront s’appeler des homologies. Les homologies peuvent se combiner comme des équations ordinaires.

Obtenir une sous-variété peu différente de la sous-variété initiale est bien utile par exemple lorsque l’on définit et que l’on calcule des nombres d’intersection (voir plus bas), afin d’obtenir que les variétés que l’on intersecte ne se rencontrent qu’en un nombre fini de points.

Poincaré appelle donc les nouveaux types d’équations qu’il manipule des homologies, probablement afin d’indiquer qu’il ne s’agit pas d’une identité d’objets d’un côté et de l’autre du signe $\sim$ de similitude, mais plutôt d’une sorte de ressemblance. Ces homologies sont néanmoins suffisamment proches des « équations ordinaires » de l’algèbre et de l’arithmétique pour se combiner comme elles.

Mais comment se « combinent » les « équations ordinaires » ?

Tout d’abord, si l’on a des équations :

$$ a + b = c + d \ \mbox{ et } \ A + B = C + D $$

alors on peut les additionner :

$$ a + b + A + B = c + d + C + D. $$

Mais on peut aussi déduire :

$$ a + b - c=d. $$

Cette dernière règle de changement de signe pose un problème d’interprétation lorsqu’on veut l’importer dans notre contexte de calcul avec des homologies entre figures géométriques. Plus précisément, si $V$ est une sous-variété, que signifie $-V$ ?

De l’importance des orientations

Eh bien, la notation $-V$ désigne la variété ayant l’orientation opposée à celle de $V$ (que Poincaré appelle la variété opposée à $V$). Ainsi, par exemple, $-2V = 2(-V)$.

Dans notre première figure manquent justement les orientations des courbes fermées $v_1,...,v_4$. Pour que la relation écrite dessus soit correcte, il faut les orienter toutes de la même manière. C’est simple de comprendre ce que cela veut dire, car il s’agit de courbes. Par exemple :

Une autre solution serait de changer simultanément les orientations des quatre cercles dans la figure précédente.

Il s’avère qu’il y a une notion analogue d’orientabilité pour les variétés de dimension quelconque. Il est important d’introduire cette notion, car à partir de la dimension deux il existe des variétés non-orientables, généralisations de la bande de Möbius.

Dans le cas du cercle, on voit que l’on a exactement deux orientations possibles, correspondant au fait de tourner dans un sens ou dans l’autre. Ce fait est tout à fait général : si une variété de dimension quelconque est orientable alors, pourvu qu’elle soit connexe, on peut l’orienter d’exactement deux manières différentes.

Le calcul de Poincaré ne s’applique qu’aux sous-variétés orientables, et pour lesquelles on a de plus choisi l’une des deux orientations possibles. C’est ce choix d’orientation qui permet de discerner une sous-variété $W$ de son opposée $-W$. Insistons : une lettre $W$ représente donc dans le calcul des homologies non seulement une sous-variété, mais en plus un choix d’orientation pour celle-ci, parmi les deux choix possibles.

Mais imposer que les règles du calcul des homologies imitent fidèlement celles de l’algèbre usuelle oblige à élargir la notion de variété, comme le montre l’exemple suivant :

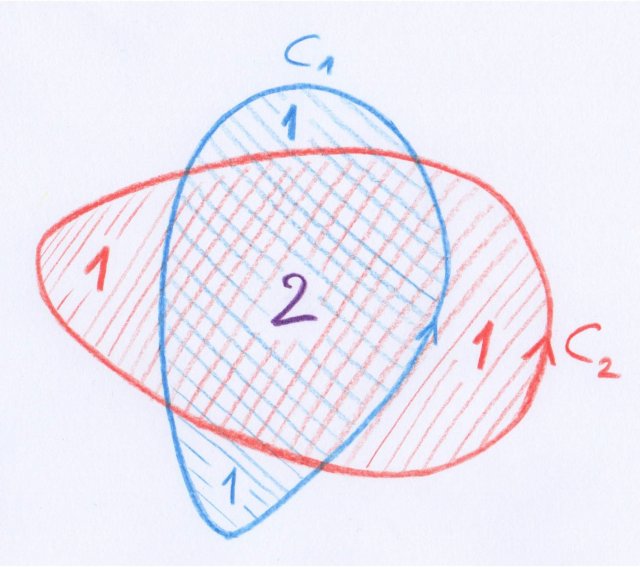
Dans ce dessin, $C_1$ et $C_2$ représentent deux courbes fermées orientées, situées dans un même plan. Chacune borde un disque, donc $C_1 \sim 0$ et $C_2 \sim 0$. Par les règles de calcul précédentes, on obtient l’homologie $C_1 + C_2 \sim 0$. Mais visiblement $C_1 + C_2$ n’est pas la frontière d’une surface lisse dans le plan. Par contre, si on travaille algébriquement, la somme $C_1 + C_2$ sera la frontière de la somme des deux disques orientés de la même manière, qui contient 2 fois la partie commune des deux disques et 1 fois chacune des quatre autres « oreilles ».

Des exemples semblables au précédent montrent qu’il est indispensable de se permettre de travailler avec la généralisation suivante de la notion de sous-variété d’une variété donnée : une combinaison linéaire à coefficients entiers de sous-variétés orientées $c_1 V_1 + \cdots + c_m V_m$. C’est ce que l’on appellera plus tard une chaîne (à coefficients entiers).

La notion de frontière s’étend aux chaînes. Ainsi, la frontière de $c_1 V_1 + \cdots + c_m V_m$ est la somme $c_1 F_1 + \cdots + c_m F_m$, chaque $F_i$ étant la frontière orientée de la variété $V_i$. Ceci permet d’étendre aussi la notion de variété fermée : une chaîne est dite fermée si sa frontière est nulle, c’est-à-dire que la somme des coefficients de chaque variété orientée apparaissant dans la somme précédente est nulle.

Définition des nombres de Betti

Ce sont les règles de calcul des homologies qui permettent à Poincaré de définir les nombres de Betti de la variété de départ :

Nous dirons que les variétés $v_1,v_2,...,v_{\lambda}$, d’un même nombre de dimensions et faisant partie de $V$, sont linéairement indépendantes, si elles ne sont liées par aucune homologie à coefficients entiers.

S’il existe $P_m - 1$ variétés fermées à $m$ dimensions faisant partie de $V$ et linéairement indépendantes et s’il n’en existe que $P_m - 1$, nous dirons que l’ordre de connexion de $V$ par rapport aux variétés à $m$ dimensions est égal à $P_m$.

Ainsi se trouvent définis, en ce qui concerne une variété $V$ à $m$ dimensions, $m-1$ nombres que j’appellerai $P_1, P_2,..., P_{m-1}$ et qui sont les ordres de connexion de $V$ par rapport aux variétés de $1, 2, . . . , m -1$ dimensions.

Je les appellerai dans la suite les nombres de Betti. [2]

Par la suite, c’est ce que Poincaré note $P_{m} - 1$ que l’on appela $m$-ème nombre de Betti. Nous noterons ce nombre $B_m$, pour ne pas le confondre avec celui défini par Poincaré. Ainsi, $B_m$ désigne le nombre maximal de sous-variétés (au sens élargi de chaîne fermée, c’est-à-dire sans bord) de dimension $m$ de $V$ qui sont indépendantes du point de vue des relations d’homologie.

Dans la figure suivante sont représentées deux surfaces fermées et sur chacune d’entre elles un système maximal de courbes fermées indépendantes. Cela serait trop long d’expliquer ici pourquoi cette affirmation est correcte. En l’admettant, on a une illustration du fait que le premier nombre de Betti $B_1$ vaut $2$ pour le tore (surface de gauche) et $8$ pour la surface de droite.

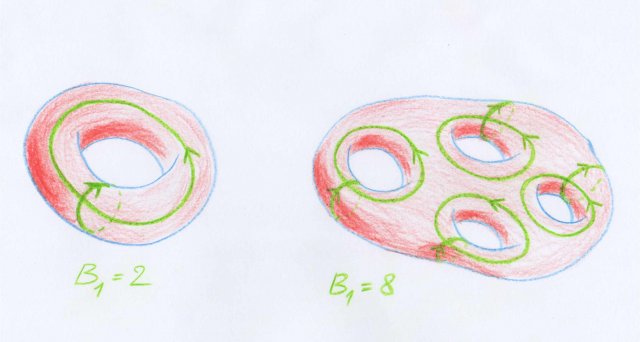
Ayant défini les nombres de Betti, nous voici prêts à voir comment Poincaré énonça son théorème de dualité.

L’énoncé du théorème de dualité de 1895

C’est dans son article « Analysis Situs » que Poincaré formula aussi pour la première fois sous forme d’un énoncé spécifique, et non pas d’une remarque faite en passant (nous y reviendrons dans la dernière section) ce que l’on allait appeler son théorème de dualité :

Pour une variété fermée, les nombres de Betti également distants des extrêmes sont égaux.

Ainsi, le théorème de dualité de Poincaré affirme que dans une variété fermée et orientable de dimension $n$, il y a autant de sous-variétés indépendantes (du point de vue des relations d’homologie) d’une dimension donnée $p$ que de la dimension complémentaire $n-p$. Par exemple, dans une variété de dimension $3$, il y a autant de courbes que de surfaces indépendantes.

Ce théorème est important avant tout parce qu’il indique que l’on peut faire des économies de calcul : la connaissance d’une partie des nombres de Betti détermine la partie restante. Mais il est aussi important comme prototype de théorème de symétrie interne des espaces. Par la suite, d’autres théorèmes de même nature furent recherchés et découverts.

Définition des nombres d’intersection

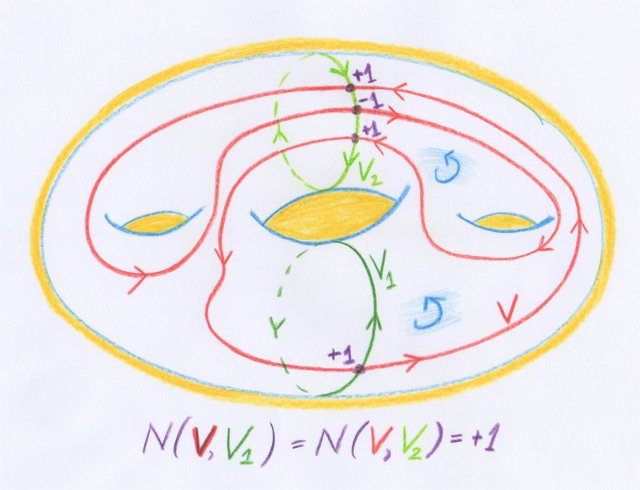
Dans le même article, Poincaré propose une démonstration du théorème de dualité. Celle-ci passe par la définition de nombres d’intersection entre variétés de dimensions complémentaires. Afin de suivre les explications qui suivent, on pourra regarder les paires de courbes $(V, V_i)$ sur le dessin illustrant la section suivante.

Supposons que l’on se trouve dans une variété ambiante $W$. Considérons deux sous-variétés $A$ et $B$ de dimensions complémentaires. Un point très important est qu’il faut que $W$, $A$ et $B$ soient simultanément orientées.

— On considère d’abord le cas où $A$ et $B$ n’ont qu’un nombre fini de points en commun, et où en aucun de ces points elles ne sont tangentes. On peut alors définir un nombre d’intersection local $N_P(A, B)$ en chacun de ces points $P$ : il vaut soit $+1$ soit $-1$, selon que l’orientation de $A$ suivie de celle de $B$ fournit ou non l’orientation de $W$. Le nombre d’intersection global $N(A, B)$ est alors la somme des nombres d’intersection locaux.

— Lorsque les sous-variétés $A$ et $B$ ont une infinité de points communs, ou bien qu’elles ont des points de tangence, on déforme d’abord légèrement l’une d’entre elles afin que les nouvelles variétés vérifient les hypothèses du cas précédent. On montre que cela est toujours possible et que le nombre d’intersection obtenu ne dépend pas du choix de la déformation.

La première démonstration de Poincaré

L’idée fondamentale de la première preuve de Poincaré de son théorème de dualité est que l’on peut déterminer si des sous-variétés fermées et orientées d’une variété fermée orientée donnée sont indépendantes du point de vue des homologies en calculant des nombres d’intersection $N(V, W)$ avec les variétés (toujours supposées fermées et orientées) de dimension complémentaire :

Si donc $V_1$ et $V_2$ sont deux variétés fermées à $n-p$ dimensions, si pour toutes les [variétés] $V$ à $p$ dimensions, on a $N(V,V_1)=N(V,V_2)$, on aura aussi $V_1 \sim V_2$ et inversement.

Dans la figure suivante est représentée la seconde implication, dans le cas de deux courbes fermées orientées, qui sont homologues sur une surface orientée. On a bien $V_1 \sim V_2$ car $V_2 - V_1$ est le bord de la partie de droite de la surface représentée, munie de l’orientation indiquée par les petites flèches recourbées sur elles-mêmes.

Poincaré explique ensuite que le théorème de dualité est une conséquence directe du théorème précédent sur les nombres d’intersection.

En effet, supposons que le nombre de Betti $a = B_p$ en une certaine dimension $p$ est strictement plus grand que le nombre de Betti $b = B_q$ en dimension complémentaire $q = n - p$. Choisissons des sous-variétés $V_1 , . . . , V_a$ de dimension $p$ indépendantes homologiquement, et d’autres $W_1 , . . . , W_b$ de dimension $q$, indépendantes elles aussi.

Considérons ensuite une combinaison linéaire :

$$X = x_1 V_1 + \cdots + x_a V_a$$

et posons le système d’équations :

$$N(X,W_1)=\cdots =N(X,W_b)=0.$$

Une propriété essentielle du nombre d’intersection est d’être linéaire par rapport à chacun des membres. Donc :

$$N(X, W_j) = x_1 N(V_1, W_j) + ... + x_a N(V_a, W_j).$$

On obtient un système d’équations linéaires et homogènes ayant, par l’hypothèse $a > b$, moins d’équations que d’inconnues. Il admet donc une solution dans laquelle tous les $x_i$ ne sont pas nuls. Fixons une telle solution.

Comme les sous-variétés $V_i$ ont été supposées indépendantes homologiquement, on déduit que $X$ n’est pas homologue à $0$. Par contre $N(X, W) = 0$ pour toute sous-variété $W$ de dimension complémentaire, car une telle variété est liée par une homologie aux sous-variétés $W_j$. Par le théorème précédent de Poincaré sur les nombres d’intersection, on déduit que $X$ est homologue à $0$, ce qui est une contradiction.

Et voilà, un nouveau théorème est né et démontré.

Mais Poincaré fut bientôt amené à préciser l’interprétation des termes mêmes de l’énoncé du théorème et à en proposer une nouvelle preuve. Pourquoi donc ? C’est ce que nous verrons dans la section suivante.

Les critiques de Heegaard

Dans sa thèse publiée en 1898, et traduite en français pendant la première guerre mondiale, Poul Heegaard critique le théorème de dualité, ainsi que la preuve qu’en donne Poincaré :

 Il donne un exemple de variété fermée orientable de dimension $3$ pour laquelle le théorème de dualité n’est pas vrai.

 Il indique une erreur dans le raisonnement de Poincaré.

La variété de dimension trois que Heegaard pense être un contre-exemple au théorème de dualité de Poincaré (qu’il étudie dans la section XIV 10 de la version française de son travail) est l’espace projectif réel, dont les points paramètrent les droites vectorielles de $\mathbb{R}^4$. Ce qui est intéressant est que Heegaard ne le présente pas du tout comme on le ferait de nos jours, soit en identifiant les points antipodes sur une sphère de dimension trois, soit en pratiquant cette même identification sur le bord d’une boule de dimension trois. En fait, il l’introduit comme bord d’un voisinage du sommet d’un cône quadratique dont on considérerait tous les points à coordonnées complexes. C’est-à-dire, comme intersection d’une sphère d’équation $| x |^2 + | y |^2 + | z |^2 =1$ et du lieu des points d’équation $ z ^2 = x^2 - y^2 $ dans l’espace affine complexe $\mathbb{C}^3$.

Comme on l’explique dans la suite, le calcul de Heegaard est basé sur une autre interprétation de la notion de nombre de Betti que celle choisie par Poincaré. Heegaard prétend que $P_1 = 2$ et $P_2 = 1$, mais avec la convention de Poincaré on a $P_1 = P_2 = 1$, donc il ne s’agit pas d’un contre-exemple. Et pour cause, car le théorème est vrai avec l’interprétation de Poincaré.

Venons-en à l’erreur de raisonnement exhibée par Heegaard dans la section XII de son article cité en bibliographie. Poincaré suppose sans justifications que toute sous-variété de codimension $p$ est intersection complète de $p$ hypersurfaces (c’est-à-dire qu’on peut trouver $p$ hypersurfaces lisses globalement transverses entre elles, et dont l’intersection se réduit à la sous-variété donnée).

Mais ceci est faux, même si les outils théoriques de l’époque ne permettaient pas d’en expliquer clairement la raison. Il fallut attendre le développement dans les années 1930 de la notion de fibré vectoriel au-dessus d’une variété, pour pouvoir donner une explication simple du fait que dans certaines variétés, il existe des sous-variétés qui ne sont pas des intersections complètes.

En effet, il suffit de remarquer que, pour les intersections complètes (les variétés et leurs sous-variétés étant toujours supposées orientables), le fibré normal peut être trivialisé globalement, c’est-à-dire que l’on peut trouver un nombre fini de champs de vecteurs continus et normaux à la sous-variété qui forment une base de l’espace normal en chaque point.

Des exemples où ceci est faux aparaissent dès le cas des surfaces dans des variétés de dimension quatre. Par exemple, si on prend comme variété ambiante l’espace $TS$ de tous les vecteurs tangents à une sphère de dimension deux $S$, le fibré normal de la sphère $S$ (identifiée au lieu des vecteurs nuls, donc vue comme sous-variété de $TS$) est isomorphe au fibré tangent $TS$. Mais « la sphère ne peut pas être peignée », c’est-à-dire que l’on ne peut même pas trouver un seul champ de vecteurs tangents continu et partout non-nul ...

Apparemment Poincaré ne réussit pas à réparer facilement cette erreur, raison pour laquelle il changea complètement de stratégie. En fait, en fondant sur d’autres bases (développées à partir de la deuxième stratégie de Poincaré, dont on discutera plus bas) le calcul des homologies et des nombres d’intersection, au XX-ème siècle on a pu faire parfaitement marcher la preuve précédente de Poincaré du théorème de dualité.

Poincaré réagit pour la première fois à ces critiques de Heegaard dans une note aux Comptes Rendus de l’Académie des Sciences de 1899 :

Ces critiques sont en partie fondées ; le théorème n’est pas vrai des nombres de Betti tels que Betti les définit ; [...].

Le théorème est vrai, au contraire, des nombres de Betti tels que je les définis ; j’en ai trouvé une démonstration qui est fondée sur la considération des
polyèdres à $n$ dimensions et que je développerai prochainement dans un Mémoire plus étendu.

Voici comment il explique la différence des deux définitions :

Le $p$-ème nombre de Betti diminué d’une unité est le nombre de variétés à $p$ dimensions distinctes faisant partie de la variété donnée. Mais il reste à définir ce que l’on doit entendre par variétés distinctes. Pour Betti, plusieurs variétés $v_p$ sont distinctes quand il n’existe pas dans la variété donnée de variété à $p + 1$ dimensions dont la frontière complète soit formée par l’ensemble des variétés $v_p$. Dans la définition que j’ai adoptée, les variétés $v_p$ ne sont dites distinctes que s’il n’existe pas de variété à $p + 1$ dimensions dont la frontière complète soit formée par l’ensemble des variétés $v_p$, répété une ou plusieurs fois.

Cette citation peut sembler quelque peu obscure. Nous consacrerons la section suivante à son éclaircissement.

La morale de cette histoire est, selon Poincaré, que le contre-exemple de Heegaard n’en est pas un. Heegaard n’a simplement pas utilisé la définition correcte des nombres de Betti, celle qui rend le théorème vrai.

Quant à la deuxième critique de Heegaard, Poincaré la juge fondée, ce qui le mène à changer de stratégie de preuve. Nous découvrirons la nouvelle stratégie après avoir comparé les deux définitions des nombres de Betti dont parle Poincaré.

Les deux définitions des nombres de Betti

Le point-clé de la citation précédente est contenu dans le syntagme « répété une ou plusieurs fois ».

Qu’est-ce que cela veut dire ? Poincaré s’expliqua plus amplement dans l’article « Complément à l’Analysis Situs », paru en 1899 : il permet des « homologies avec division ». Voici comment il introduit cette notion :

Nous conviendrons également qu’il est permis de diviser une homologie par un nombre entier, quand tous les coefficients sont divisibles par cet entier. Par conséquent, s’il y a une variété à $p + 1$ dimensions, dont la frontière complète sera constituée par quatre fois la variété $v_1$, nous conviendrons qu’on peut écrire non seulement l’homologie $4v_1 \sim 0$, mais encore l’homologie $v_1 \sim 0$ ; de sorte que cette homologie signifie qu’il y a des variétés à $p + 1$ dimensions, qui admettent pour frontière complète la variété $v_1$ ou un certain nombre de fois cette variété.

Lorsqu’on lit les définitions de l’article « Analysis Situs » de 1895, on a l’impression qu’une relation :

$$a_1 v_1 + a_2 v_2 \ + \ ... \ + \ a_k v_k \sim 0$$

signifie que les sous-variétés orientées $v_1,...,v_k$, la $i$-ème étant comptée $a_i$ fois, forment la frontière complète d’une sous-variété (au sens généralisé de chaîne, comme nous l’avons expliqué précédemment), ayant une dimension de plus.

Mais si on parcourt attentivement les exemples de Poincaré, on voit qu’il se permettait de déduire algébriquement que l’on a cette relation dès que l’on a obtenu une homologie de la forme :

$$ a \cdot a_1 v_1 \ + \ a \cdot a_2 v_2 \ + \ ... \ + \ a \cdot a_k v_k \sim 0$$

pour un certain entier non-nul $a$. Cette règle de division n’ayant pas été formulée dès le départ, Heegaard n’a pas perçu qu’en fait Poincaré se l’imposait dans la définition des nombres de Betti. Nous devons donc la rajouter aux règles de « combinaison des équations ordinaires », discutées précédemment.

Nous sommes donc face à deux définitions. Qu’est-ce qui peut nous faire préférer l’une plutôt que l’autre ? Et bien, le fait que l’une vérifie des lois plus simples ou plus élégantes que l’autre. La dualité de Poincaré est une telle loi. Le fait que la définition selon Poincaré la vérifie, mais pas celle selon Betti est un argument fort pour préférer la première. C’est ce qui a été fait au XX-ème siècle !

La deuxième stratégie de preuve de Poincaré

Nous avons vu que Heegaard critique aussi la preuve de Poincaré. Ce dernier trouve cette deuxième critique pertinente, et pour y remédier, il change complètement de stratégie. Plus précisément, il propose une deuxième approche de la définition des nombres de Betti et de la démonstration du théorème de dualité, en imaginant la variété décomposée en polyèdres, comme si on l’avait cassée en morceaux qui auraient ensuite été réassemblés par un archéologue minutieux :

Considérons donc [...] un polyèdre à $p$ dimensions, c’est-à-dire une variété $V$ à $p$ dimensions, divisée en variétés $v_p$ ; les frontières des $v_p$ ,
seront les $v_{p-1}$, celles des $v_{p-1}$ les $v_{p-2}$, [...] je me proposerai d’abord de déterminer le nombre $P_{q-1}$ des variétés à $q$ dimensions, fermées et linéairement indépendantes, que l’on peut tracer sur notre polyèdre $V$, mais en nous bornant à celles qui sont des combinaisons des variétés $v_q$.

Par exemple, voici une surface polyédrale :

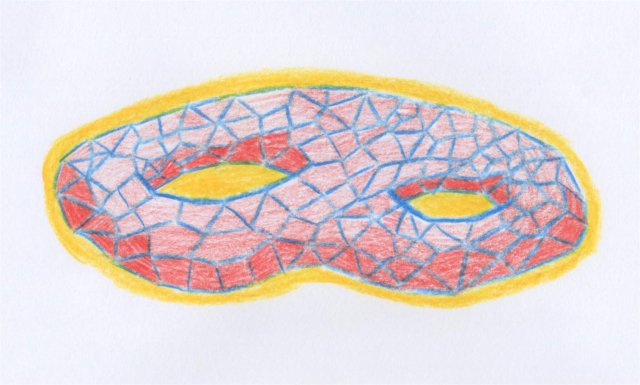
En présence d’une variété munie d’une structure de polyèdre, Poincaré ne se permet plus de travailler avec n’importe quelle sous-variété, qui est ensuite libre de se mouvoir continûment, mais s’astreint à ne considérer que des sous-variétés composées des faces de dimension convenable de la structure polyédrale choisie. Ces sous-variétés (en fait des chaînes) sont donc des combinaisons linéaires de l’ensemble fini des faces de la décomposition polyédrale.

Remarquons que la notion de variété change de cette manière une nouvelle fois : si on pensait pouvoir ne manipuler avec la première stratégie que des sous-variétés lisses ayant des bords lisses eux aussi (combinées ensuite linéairement dans les chaînes), avec la deuxième on est forcé de manipuler des variétés ayant des bords lisses par morceaux, analogues de dimension quelconque des polygones.

L’idée de base de la nouvelle preuve du théorème de dualité est que, chaque fois que l’on a une structure de polyèdre sur une variété fermée, on en a une deuxième qui lui est réciproque, et qui est bien définie à déformation près.

Ceci est illustré dans la figure suivante pour le cas des surfaces. En partant de la décomposition polyédrale bleue, la décomposition orange lui est réciproque. De plus, et c’est cela qui fait parler de dualité, la décomposition bleue est à son tour réciproque de la décomposition orange.

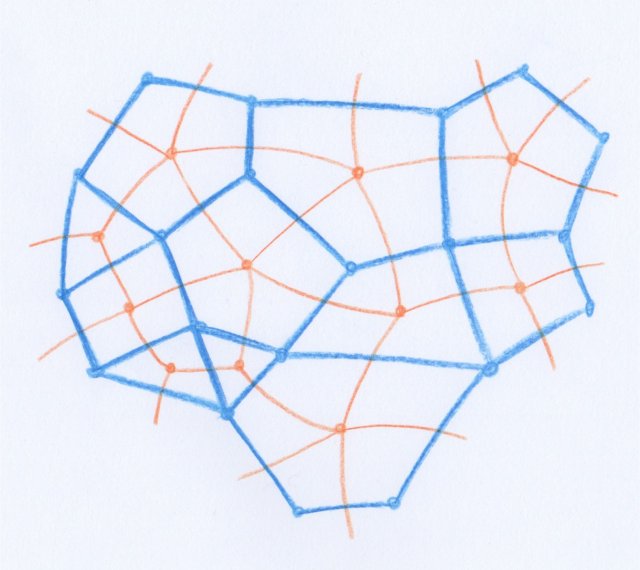
En restant en dimension $2$, on peut penser à une structure de polyèdre sur une surface comme à une décomposition de celle-ci en pays [3]. Imaginons alors que chaque pays a une capitale. On relie les capitales par des routes directes chaque fois que deux pays partagent une frontière de dimension $1$, la route traversant cette frontière. Ce sont ces routes qui décomposent la surface de la manière duale à la décomposition initiale en pays. On comprend bien que cette décomposition n’est pas unique, car le choix des capitales, puis des routes qui les relient, ne l’est pas. Mais il l’est à déformation près, comme on invite le lecteur à se convaincre en faisant quelques dessins.

Une telle construction peut s’étendre en dimension quelconque $n$. Pour chaque face de dimension $p$ de la première décomposition polyédrale, il existe une unique face de dimension complémentaire $n-p$ de la décomposition duale qui l’intersecte. Cette bijection entre faces de dimensions complémentaires des deux structures de polyèdre sur la variété initiale est la dualité géométrique visible qui est sous-jacente à la dualité plus subtile des nombres de Betti.

C’est elle qui sert de base à Poincaré pour sa nouvelle approche de la démonstration du théorème de dualité des nombres de Betti. Plus précisément, il développe la stratégie de preuve suivante :

 Toute variété admet une structure de polyèdre.

 Les nombres de Betti tels qu’il les définit sont les mêmes que ceux calculés à partir d’un polyèdre.

 Les nombres de Betti polyédraux restent inchangés lorsqu’on subdivise un polyèdre.

 Deux polyèdres réciproques ont une subdivision commune.

 Un nombre de Betti calculé à partir d’un polyèdre est égal au nombre de Betti complémentaire calculé à partir du polyèdre réciproque.

Même si ses arguments ne sont pas complets, tous ces énoncés sont vrais, et l’on a pu faire marcher cette stratégie exactement [4] comme l’avait pensée Poincaré !

Source de la différence entre les deux définitions

Tout cela est bien joli. Mais Poincaré reste préoccupé par le problème de la différence entre sa définition des nombres de Betti et celle donnée par Betti. Dans le « Second complément à l’Analysis Situs », paru en 1900, il explique que cette différence est due à un phénomène de torsion de la variété, qu’il arrive même à mesurer. Cette mesure part de la considération de certains « tableaux » de nombres.

Nous reconnaissons dans ces tableaux des matrices. Mais, même si le terme de « matrice » existait depuis le milieu du XIX-ème siècle, Poincaré ne l’utilise pas. Néanmoins, comme les temps ont bien changé de ce point de vue, nous collerons à l’usage moderne en l’employant librement.

Il s’agit ici simplement des matrices d’incidence entre faces de dimensions successives du polyèdre. Expliquons comment ces matrices sont construites à l’aide d’un exemple.

Dans la figure suivante est représentée la matrice d’incidence des faces de dimension $1$ et $2$ de la décomposition polyédrale de gauche, consistant en un quadrilatère et un triangle ayant une arête commune. Les faces et les arêtes sont orientées comme indiqué sur la figure. Ensuite, pour chaque couple formé d’une face et d’une arête, on marque $0$ si l’arête n’est pas contenue dans la frontière de la face, $+1$ si elle y est contenue avec l’orientation compatible avec celle de la face et $-1$ si elle a l’orientation opposée [5].

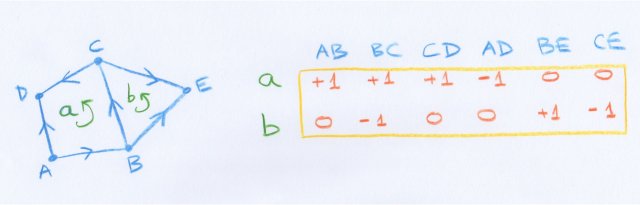
Poincaré montre que par des opérations élémentaires sur les lignes et les colonnes (additions, soustractions, changements de signes et permutations), on peut se ramener à une matrice qui a tous ses éléments nuls en dehors de la diagonale principale et que, pris dans l’ordre, chaque élément de cette diagonale divise le suivant. Il appelle invariants du tableau cette suite d’entiers de la diagonale.

C’est parmi les invariants des tableaux que se trouvent les nombres qui permettent de mesurer la torsion de la variété :

Cela posé, revenons à nos tableaux [...] et à leurs invariants, et en particulier à ceux de ces invariants qui ne sont égaux ni à $0$, ni à $1$, et que nous appellerons coefficients de torsion.

Et ce sont les coefficients de torsion qui sont source de la différence des deux définitions des nombres de Betti :

Ce qui précède montre combien il importe de distinguer deux sortes de variétés. Celles de la première sorte que j’appellerai variétés sans torsion, seront celles pour lesquelles les invariants de tous les tableaux $T_q$ sont tous égaux à $0$ ou à $1$ ; pour lesquelles, par conséquent [...] les deux définitions des nombres de Betti sont d’accord.

Nous verrons plus bas pourquoi Poincaré pensait qu’il était face à un véritable phénomène de torsion des variétés.

Un exemple de calcul en dimension trois

Afin d’illustrer le calcul des coefficients de torsion, Poincaré applique sa méthode (dans la Section 4 du Second Complément) à des variétés de dimension trois obtenues en recollant de diverses manières les faces opposées d’un cube. Ces divers cas sont semblables, et nous n’en considérerons qu’un seul, le troisième.

On part d’un cube $ABDCA'B'D'C'$, comme sur la figure suivante :

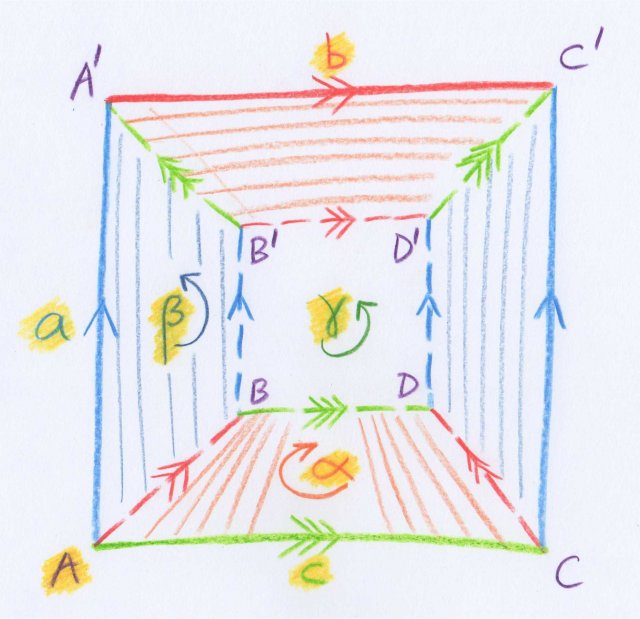
Les faces opposées sont identifiées [6] en faisant se correspondre les sommets de la manière suivante (avec les notations de l’article) :

$$(1) ABDC \equiv B'D'C'A' $$

$$(2) ABB'A' \equiv CDD'C'$$

$$(3) ACC'A' \equiv BDD'B'.$$

Ce qui nous intéresse en premier est de voir combien de faces de diverses dimensions (sommets, arêtes, disques et « cases » de dimension trois) s’obtiennent après recollement. En utilisant successivement les relations (1), (2), (3), (2), (1), (3), (2), on obtient :

$$A \equiv B' \equiv D' \equiv C' \equiv A' \equiv C \equiv D \equiv B.$$

Il y a donc un seul sommet, que nous pourrons noter encore $A$ ! De même, on voit qu’il y a trois arêtes, car on a les identifications suivantes :

$$AA' \equiv CC' \equiv BB' \equiv DD'$$

$$AB\equiv CD\equiv B'D' \equiv A'C' $$

$$AC\equiv BD\equiv D'C' \equiv B'A'.$$

Notons par $a, b, c$ ces arêtes, orientées du premier sommet au deuxième dans les expressions précédentes (voir la figure). Notons aussi par $\alpha, \beta, \gamma$ les trois faces de dimension deux, prises dans l’ordre des formules (1), (2), (3) et orientées d’après le sens de parcours de leurs sommets considérés dans ces mêmes formules. On obtient alors les trois matrices d’incidence suivantes ($T_i$ décrivant l’incidence des faces de dimension $i$ et $i -1$) :

$$T_1=(0 0 0); \ \ T_2=\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & -1 \\ 0 & 1 &1 \end{array} \right) ; \ \ T_3= \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right). $$

On allait les interpréter plus tard comme matrices des opérateurs bord $\partial$ entre groupes de chaînes de dimensions successives, calculées dans les bases formées par les faces. Expliquons par exemple comment est calculée $T_2$. Ses colonnes expriment les bords des faces de dimension deux $\alpha, \beta, \gamma$ en termes des arêtes $a,b,c$. Alors, à l’aide des identifications précédentes, on a :

$$\partial \alpha = \partial (ABDC)=AB+BD+DC+CA=b+c- b- c=0$$

$$ \partial \beta= \partial (ABB'A')=AB+BB' +B'A' +A'A=b+a+c-a=0\cdot a+1\cdot b+1\cdot c$$

$$\partial \gamma= \partial (ACC'A')=AC+CC' +C'A' +A'A=c+a-b-a=0\cdot a+(-1)\cdot b+1\cdot c.$$

On obtient bien les trois colonnes de la matrice $T_2$ ! Ensuite, en additionnant la deuxième ligne à la troisième, la dernière colonne à la deuxième, en changeant le signe de
la dernière colonne et enfin en permutant certaines lignes et colonnes, on se ramène à la matrice suivante :

$$\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{array} \right).$$

Elle a donc un seul invariant de torsion, égal à $2$.

Une extension du théorème de dualité

Poincaré formule alors une extension du phénomène de dualité aux coefficients de torsion :

Les tableaux également distants des extrêmes ont mêmes coefficients de torsion.

Ici les tableaux sont pensés écrits l’un à la suite de l’autre, dans l’ordre croissant ou décroissant des dimensions concernées. La distance aux extrêmes est mesurée dans cette file. Ainsi, pour l’exemple de la section précédente, $T_1$ et $T_3$ sont également distants des extrêmes.

Poincaré base aussi la preuve de ce nouveau théorème sur la considération des polyèdres réciproques, convenablement orientés, via les pas suivants :

 Une matrice d’incidence d’une structure polyédrale est égale à la transposée de la matrice d’incidence complémentaire d’une structure polyédrale duale.

 Une matrice et sa transposée ont mêmes invariants.

 Les coefficients de torsion sont inchangés par subdivision. Ce qui permet de conclure en utilisant le fait qu’une décomposition polyédrale et l’une quelconque de ses subdivisions duales ont une subdivision commune.

Venons-en à la raison pour laquelle Poincaré a choisi le terme de « torsion ». Il l’explique de la manière suivante :

Si un polyèdre a tous ses tableaux bilatères, c’est-à-dire si l’on ne peut pas composer avec ses éléments une variété unilatère, ce polyèdre n’a pas de coefficients de torsion. On voit que l’existence des coefficients de torsion [...] est due à ce fait que les éléments du polyèdre peuvent engendrer des variétés unilatères, c’est-à-dire que le polyèdre est pour ainsi dire tordu sur lui-même. C’est ce qui justifie l’expression de coefficients de torsion, ou celle de variétés avec ou sans torsion.

C’est en dimension deux que l’on peut composer pour la première fois une variété unilatère avec des faces de polyèdres, lorsque l’on fabrique une bande de Möbius. Cette dernière est donc le prototype de variété tordue. On comprend alors le choix du terme : il faut tordre une bande de papier avant de recoller ses extrémités pour fabriquer une bande de Möbius.

Afin d’illustrer les considérations de cette section, reprenons l’exemple de la variété de dimension trois de la section précédente.

D’après le critère découvert par Poincaré, il doit donc y avoir une surface non-orientable obtenue en joignant de proche en proche des faces de dimension $2$. Trouvez-en une !

Hélas, dans ce cas la dualité des invariants de torsion ne dit rien : le premier et le troisième tableau ont toujours des invariants de torsion nuls en dimension trois, par le même critère de Poincaré, et c’est une évidence que $T_2$ a les mêmes invariants que $T_2$. De même qu’il faut attendre d’être en dimension $3$ pour voir la dualité des nombres de Betti, il faut attendre d’être en dimension $4$ pour voir celle des invariants de torsion.

Au fait, ici le premier et le deuxième nombre de Betti sont tous les deux égaux à $1$ : $a$ forme une base du groupe d’homologie avec divisions (« à coefficients rationnels » dit-on de nos jours) de dimension $1$ et $\alpha$ une base de celui de dimension $2$. En effet, les opérations décrites précédemment reviennent à dire que l’on prend $(b - c, c, a)$ comme base du groupe des chaînes de dimension $1$ et $(-\gamma, \beta + \gamma, \alpha)$ comme base de celui des chaînes de dimension $2$. La matrice de l’opérateur bord est dans ces bases la dernière écrite précédemment. En particulier, $2c$ est un bord (de $\beta + \gamma$) et les seules chaînes de dimension $2$ qui n’ont pas de bord sont les multiples de $\alpha$.

Quelques aperçus sur l’évolution ultérieure du théorème

Avant de passer aux prédécesseurs, donnons à présent quelques renseignements sur l’évolution du théorème et du langage utilisé pour l’exprimer au cours du XX-ème siècle.

L’utilisation par Poincaré du terme de « torsion » est à l’origine de l’emploi moderne du terme de « sous-groupe de torsion » d’un groupe abélien, c’est-à-dire du sous-groupe des éléments dont un multiple entier est nul.

Ici il s’agit des groupes d’homologie à coefficients entiers (appellation de la fin des années 1920), constitués des cycles modulo les frontières. Les coefficients de torsion du $q$-ème tableau sont alors réinterprétés en tant qu’invariants de torsion du $(q - 1)$-ème groupe d’homologie (attention au décalage de l’indice !).

On arrive ainsi à l’explication moderne de la différence des deux définitions des nombres de Betti :

 Selon Betti (interprété par Poincaré) : c’est le nombre minimal de générateurs du groupe d’homologie correspondant.

 Selon Poincaré : c’est le nombre minimal de générateurs du quotient du groupe par son sous-groupe de torsion.

Dans le développement ultérieur de la théorie on allait combiner les deux approches de Poincaré, en construisant les groupes d’homologie à l’aide de morceaux de polyèdres, éventuellement singuliers, contenus dans la variété, et en montrant qu’ils permettent de définir des nombres d’intersection. L’un des énoncés modernes du théorème de dualité est alors que le produit d’intersection $N : H_p \times H_q \to \mathbb{Q}$ entre groupes d’homologie à coefficients rationnels de dimension complémentaire d’une variété fermée et orientée est non-dégénéré.

Travailler à coefficients rationnels fait perdre l’information sur la torsion. Mais l’avantage de ce point de vue en termes de structures algébriques est que l’on obtient une généralisation du fait, illustré dans la section « Définition des nombres de Betti », que le premier nombre de Betti d’une surface fermée et orientable est pair : $B_{2k+1}$ est pair pour toute variété fermée et orientable de dimension $4k + 2$. En effet, pour des dimensions de ce type, le produit d’intersection est antisymétrique : $N(V, W) = - N(W,V)$. Le fait qu’il soit non-dégénéré (on dit alors qu’il est symplectique) force la dimension à être paire !

Il y a en fait une version à coefficients dans tout anneau commutatif de la dualité de Poincaré. En particulier à coefficients dans le corps à deux éléments $\mathbb{Z}/ 2 \mathbb{Z}$. Ce dernier a l’avantage de ne plus nécessiter d’orienter les faces d’une décomposition polyédrale, puisque l’on a automatiquement $A = -A$ pour toute face orientée $A$. Cela donne une version de la dualité de Poincaré pour les variétés fermées quelconques, pas nécessairement orientables !

La suite des matrices $T_i$, interprétée comme suite des matrices d’applications bord entre groupes de chaînes de dimensions successives, vérifie le fait que les produits successifs $T_{i-1} T_i$ sont tous nuls. On a appelé une suite d’espaces vectoriels ou, plus généralement, de modules sur un anneau, reliés par des applications linéaires qui vérifient ces propriétés, un complexe de chaînes. Et dès qu’on en a un, on peut parler de cycles et de bords, ainsi que de groupes d’homologie. Au XX-ème siècle on a appris à reconnaître cette structure algébrique de complexe de chaînes un peu partout, et il y a désormais pléthore de théories homologiques dans les maths !

Le contexte historique

Venons-en aux prédécesseurs de Poincaré, afin de mieux mettre en évidence son apport par rapport au contexte historique. Nous examinerons plus spécialement :

 Si le théorème avait déjà été formulé.

 Comment Betti définissait ses nombres.

Lorsque Poincaré publia en 1895 l’article « Analysis Situs », il pensait le théorème connu, mais jamais énoncé :

Ce théorème n’a, je crois, jamais été énoncé ; il était cependant connu de plusieurs personnes qui en ont même fait des applications.

Poincaré lui-même avait déjà utilisé le théorème en passant en 1893, dans une note aux Comptes Rendus de l’Académie des Sciences, afin de prouver que la caractéristique d’Euler [7] d’un polyèdre de dimension impaire est nulle :

Comme les nombres de Betti $P_q$ et $P_{n-q}$ sont égaux, [...] [8].

En fait, Émile Picard avait déjà énoncé le théorème en 1889, dans son « Mémoire sur la théorie des fonctions algébriques de deux variables » :

Pour un domaine fermé, les différents nombres $p_m$, pour les diverses valeurs de $m$, s’associent deux à deux, et l’on démontre que $p_m = p_{n-m}$.

Mais peut-être n’est-ce pas le même théorème ? Maintenant que nous sommes avertis de la subtilité liée à la définition des nombres de Betti pour que le théorème de dualité soit correct, il est d’autant plus important de comprendre comment Picard définissait ces nombres. Voici ce qu’il écrit :

Nous considérons un continuum fermé $\delta$ à $n$ dimensions [...] si l’on peut imaginer dans $\delta$ un nombre $p_m$ d’espaces fermés à $m$ dimensions, qui ne puissent pas constituer le contour d’un espace fermé à $m + 1$ dimensions contenu dans $\delta$, mais tel que tout autre espace fermé à $m$ dimensions puisse constituer avec une partie d’entre eux ou avec tous le contour d’un espace fermé à $(m + 1)$ dimensions contenu dans $\delta$, on dit que le domaine $\delta$ a une connexion de $m$-ème espèce $p_m + 1$.

Cette définition est presque la traduction mot à mot de ce qu’écrit Enrico Betti dans son article « Sopra gli spazi di un numero qualunque de dimensioni », publié en 1871 :

Se invece in $R$ si può imaginare un numero $p_m$ di spazi chiusi di $m$ dimensioni che non possano formare il contorno di una parte linearmente connessa di uno spazio di $m + 1$ dimensioni, tutta cuanta contenuta in $R$, e tali che ogni altro spazio chiuso di $m$ dimensioni formi solo o con una parte di essi o con tutti il contorno di una parte linearmente connessa di uno spazio di $m + 1$ dimensioni tutta quanta contenuta in $R$, diremo che $R$ ha di $(p_m + 1)^{esimo}$ ordine la connessione di $m^{esima}$ specie. [9]

Pourtant Picard ne cite pas Betti, il écrit seulement :

Mais auparavant il est indispensable de rappeler rapidement la définition des divers ordres de connexité dans la Géométrie à $n$ dimensions.

Si Picard dit qu’il rappelle la définition, c’est qu’il la considère connue. La grande ressemblance structurelle des deux textes laisse penser que Picard a utilisé directement l’article de Betti. Pourquoi ne le cite-t-il pas ? Était-il pressé par les délais du concours auquel il participait, et n’a-t-il plus revu le texte avant publication ? Pensait-il que Betti la prenait à son tour d’une autre source ?

En tout cas, tout cela ne nous explique pas comment l’existence d’un phénomène de dualité a été découverte, ni par qui.

Une piste nous est peut-être offerte par le fait que la première preuve de Poincaré passe par la considération des nombres d’intersection de sous-variétés de dimensions complémentaires. Cela permet de penser [10] que le phénomène est apparu en méditant sur un théorème (incorrect [11]) que Betti énonce au sujet des sous-variétés de dimensions complémentaires. Précisons que Betti appelle simplement connexe toute variété (pouvant avoir une frontière) telle que toute sous-variété est frontière complète d’une autre [12].

Per rendere semplicemente connesso, mediante sezioni trasverse semplicemente connesse, uno spazio finito $R$ di $n$ dimensioni, è necessario e sufficiente di fare $p_{n-1}$ sezioni lineari, $p_{n-2}$ di due, $p_{n-3}$ di tre, ... ,
$p_1$ di $n -1$ dimensioni [...]. [13]

Ainsi, Betti énonce que l’on peut rendre simplement connexe une variété qui ne l’est pas, en pratiquant des coupures successives (le long de sections transverses), et il propose une estimation du nombre de coupures nécessaires, dimension par dimension, en termes de ses nombres. Il affirme ainsi avec optimisme qu’en toutes dimensions a lieu ce que Bernhard Riemann avait prouvé pour les surfaces en 1851.

Nous finirons notre récit par une brève explication de ce théorème de Riemann.
Dans la figure suivante est illustrée la manière de découper une surface pour la rendre simplement connexe. Les cercles verts sont indépendants du point de vue des relations d’homologie et le deuxième nombre de Betti $B_2$ vaut 2 (selon les deux conventions, car dans ce cas il n’y a pas de torsion). D’autre part, on a bien besoin de 2 coupures pour rendre la surface simplement connexe ...

Betti avait en fait longuement discuté de cela avec Riemann vers 1864, comme il ressort de deux lettres qu’il a envoyées à son ami Tardy [14]. En lisant ces lettres et les notes posthumes de Riemann concernant l’Analysis situs, il n’est pas clair si c’est Betti ou Riemann qui a proposé une stratégie analogue de découpage des variétés de toutes dimensions. En tout cas, on y apprend que Gauss avait suggéré à Riemann d’analyser les surfaces en les ramenant à des surfaces plus simples par découpage ...

Poincaré a donc fait beaucoup, mais en continuant une tradition d’interrogations sur la structure des espaces. Cela illustre bien que les mathématiques sont une course de longue haleine, de génération en génération !