Commentaires sur le §6 du cinquième complément

Dans ce paragraphe crucial, Poincaré rassemble tous les outils introduits dans le cinquième complément pour définir enfin sa sphère d’homologie. En voici les différentes étapes :

• Du début jusque là, Poincaré considère une variété fermée $V$ de dimension $3$ ayant un squelette rectiligne dont les sommets sont successivement un point critique d’indice $0$, $p$ point critiques d’indice $1$, $p$ point critiques d’indice $2$, et un point critique d’indice $3$. Il déduit du paragraphe précédent que cette variété est l’union de deux corps en anses de genre $p$, notés $V'$ et $V''$, partageant le même bord $W$. Sur ce bord $W$, Poincaré distingue deux familles de $p$ courbes fermées $K_1',...,K_p'$ et $K_1'',...,K_p''$, qui sont des familles maximales de courbes de compression pour $V'$ et $V''$ respectivement.
• De Considérons maintenant à Tout cycle de $V$ est équivalent à un cycle de $W$, Poincaré montre que le morphisme $\pi_1(W)\to\pi_1(V)$ induite par l’inclusion est surjective.
• De Maintenant entre les cycles à C.Q.F.D., il montre plus précisément que

  $$\pi_1(V)=\pi_1(W)/\langle K'_1,...,K'_p,K''_1,...,K''_p\rangle.\qquad(*)$$

• De Possédant ainsi toutes les équivalences possibles à ne s’annulent pas, il en déduit, par abélianisation, la forme du groupe d’homologie $H_1(V)$ en fonction du déterminant et du rang de la matrice donnant la décomposition des courbes $K'_1,...,K'_p,K''_1,...,K''_p$ dans la base $C_1$,...,$C_{2p}$ introduite dans le §3.

La fin du §6 (et le but de l’article) consiste à présenter un exemple où le groupe d’homologie $H_1(V)$ est trivial, alors que le groupe fondamental $\pi_1(V)$ ne l’est pas. Pour cela,

• de Revenons au cas à nous donnera V, Poincaré définit à l’aide d’un diagramme deux paires de lacets $K'_1$, $K'_2$ et $K''_1$, $K''_2$ sur une surface $W$ de genre $2$, destinées à être des familles maximales de courbes de compression pour deux corps en anses $V'$ et $V''$ de bord commun $W$ et dont l’union $V$ est la sphère d’homologie recherchée.
• de On s’en rendra mieux compte à $K_1',K_2'$, Poincaré revient sur la définition de $V$ et montre que l’on peut tout aussi bien l’obtenir en échangeant les rôles de $V$ et $V'$. Il semble vouloir expliquer que l’on a bien un diagramme de Heegaard, c’est-à-dire que $W$ découpée le long de chaque paire de lacets est une sphère à 4 trous, ce qui est évident pour la première paire et un corollaire de ce qu’il dit pour la deuxième paire.
• de Cherchons à exprimer à groupe icosaédrique, Poincaré décompose $K'_1$, $K'_2$, $K''_1$ et $K''_2$ en terme des lacets fondamentaux $C_1,...,C_4$ grâce à l’algorithme du §4, en déduit grâce à (*) une première présentation du groupe fondamental de $V$, qui lui permet de montrer que $H_1(V)$ est trivial, puis, après simplification, que $\pi_1(V)$ ne l’est pas, puisqu’il se surjecte dans le « groupe icosaédrique ».
• Poincaré conclut par sa fameuse conjecture, qui est en fait ici une question : une variété fermée de dimension $3$ simplement connexe (au sens moderne, pas celui de Poincaré) est-elle nécessairement homéomorphe à la sphère ?

Scindement de Heegaard associé à un squelette rectiligne

Comme annoncé au début des commentaires du §5, Poincaré considère une variété $V$ fermée de dimension $3$, qui admet une fonction de Morse dont le squelette est un graphe rectiligne ayant pour sommets successifs un point critique d’indice $0$, $p$ points critiques d’indice $1$, $p$ points critiques d’indice $2$ et un point critique d’indice $3$. Il note

$$t_0 < t_1 < ... < t_p < t'_p <...< t'_1 < t'_0$$

les valeurs critiques associées à ces points. Sans perte de généralité, il supposer que $t_0=0$, $t'_0=1$ et $t_p < 1/2 < t'_p$.

Vu le paragraphe précédent, et par symétrie $q\leftrightarrow 3-q$ sur les indices, à chaque demi-squelette correspond un corps en anses de genre $p$. Poincaré nomme ces deux corps en anses $V'$ et $V''$, et note $W$ leur frontière commune, une surface fermée de genre $p$. La variété $V$ que considère Poincaré (attention, $V$ désigne maintenant la variété fermée, et non plus l’un des deux corps en anses comme dans le §5) possède donc un scindement de Heegaard de genre $p$.

Sur $W$, on a cette fois-ci deux systèmes de courbes $K_1',...,K_p'$ et $K_1'',...,K_p''$, familles maximales de courbes de compression pour $V'$ et $V''$ respectivement, comme définies dans le §5. Poincaré les appelle « cycles principaux » de $V'$ et $V''$ respectivement.

Surjectivité de $i_*:\pi_1(W)\to\pi_1(V)$

La surjectivité du morphisme $i_*:\pi_1(W)\to\pi_1(V)$ et la forme de son noyau, étudiée dans le paragraphe suivant, s’obtiennent simultanément si l’on utilise un argument de type Van Kampen présenté ici ou là.

Voyons maintenant l’argument de Poincaré. Tout lacet de $V$ étant homotope à un produit de lacets entièrement contenus soit dans $V'$, soit dans $V''$, et ces deux situations étant équivalentes, il suffit de montrer que tout lacet $C$ de $V'$ est homotope à un lacet de $W$, comme nous l’avions annoncé dans les commentaires du §5.

Notons $t$ le niveau minimal par lequel passe $C$. Quitte à perturber un peu $C$, on peut supposer que $t$ n’est pas une valeur critique de la fonction de Morse, et on note $q$ l’unique entier compris entre $0$ et $p$ tel que $t_q < t < t_{q+1}$. On procède par récurrence sur $p-q$.

Si $p-q=0$, alors $C$ est tout entière comprise entre les niveaux $t$ et $1/2$ entre lesquels il n’y a pas de niveau critique. Ce que Poincaré explique alors en ses termes, c’est que cette région se rétracte par déformation sur le niveau régulier $1/2$ (comme expliqué ici), donc $C$ est homotope à une courbe incluse dans $W$.

Supposons maintenant $q < p-1$. On peut décomposer $C$ en une union finie d’arcs inclus les uns entre les niveaux $t_{q+1}$ et $1/2$ et les autres entre les niveaux $t_q$ et $t_{q+1}$. Il s’agit de vérifier que les arcs du second type sont homotopes dans $V'$, à extrémités fixées, à des arcs inclus dans le niveau $t_{q+1}$. En remplaçant les anciens arcs par les nouveaux, on obtiendra, quitte à pousser encore un peu au-dessus du niveau $t_{q+1}$, un nouveau lacet homotope au précédent mais contenu strictement au dessus du niveau $t_{q+1}$, ce qui conclura la récurrence. L’argument de Poincaré repose sur le fait que du niveau $t_q+\epsilon$ au niveau $t_{q+1}+\epsilon$, la topologie change, certes, mais dans le sens d’une augmentation de l’ordre de connexion. En termes modernes, on peut vérifier, grâce à la théorie de Morse, que la région entre les niveaux $t$ et $t_{q+1}$ se rétracte par déformation sur le niveau $W(t_{q+1})$. En effet, tout se passe au voisinage du point critique. Un voisinage du point critique dans $\cup_{s=t}^{t_{q+1}} W(s)$ est un « cône plein tronqué ». Ce dernier se rétracte par déformation sur son bord conique, qui est un voisinage du point critique $W(t_{q+1})$. C’est exactement ce dont nous avions besoin

Présentation du groupe fondamental

Vu le paragraphe précédent, pour montrer que

$$\pi_1(V)\simeq\pi_1(W)/\langle K'_1,...,K'_p,K''_1,...,K''_p\rangle,$$

il ne reste plus qu’à prouver que le noyau de $i_*:\pi_1(W)\to\pi_1(V)$ est le sous groupe distingué $\langle K'_1,...,K'_p,K''_1,...,K''_p\rangle$. Pour cela, Poincaré explique qu’un lacet homotopiquement trivial dans $V$ est homotope à une combinaison de lacets homotopiquement triviaux dans $V'$ et de lacets homotopiquement triviaux dans $V''$, auxquels il peut appliquer les résultats du §5 pour conclure.

Alternativement on peut voir, comme dans nos commentaires du §5, la variété fermée $V$ comme le corps en anses $V'$ auquel on a attaché $p$ anses d’indice $2$ le long des $K''_1,...,K''_p$, puis une anse d’indice $3$ au bord sphérique restant. On a montré au §5 que $\pi_1(V')=\pi_1(W)/\langle K'_1,...,K'_p\rangle$, et les attachements des anses d’indice $2$ ont pour effet rendre triviales les classe des lacets $K''_1,...,K''_p$ dans $\pi_1(V)$ (toujours par un argument de type Van Kampen). Il en résulte comme annoncé que $\pi_1(V)\simeq\pi_1(W)/\langle K'_1,...,K'_p,K''_1,...,K''_p\rangle.$

Calcul de l’homologie en terme des courbes de compression

Possédant ainsi toutes les équivalences possibles, il est aisé d’en déduire toutes les homologies sans division possibles ; il suffit d’intervertir l’ordre des termes dans les premiers membres de ces équivalences.

Autrement dit, grâce au théorème de Hurewicz, on déduit de ce qui précède que

$$H_1(V)=H_1(W)/\langle K'_1,...,K'_p,K''_1,...,K''_p\rangle,$$

où ici le dénominateur désigne le $\mathbb{Z}$-module engendré par les classes d’homologie de $K'_1,...,K'_p,K''_1,...,K''_p$ dans $W$. Or $H_1(W)$ s’identifie à $\mathbb{Z}^{2p}$ grâce à la base « fondamentale » $(C_1,..., C_{2p})$ construite au §3 à partir de la fonction de Morse considérée, et pour étudier le quotient, il s’agit d’étudier la matrice carrée $M\in M_{2p}(\mathbb{Z})$ formée des composantes des $2p$ courbes $K'_1,...,K'_p,K''_1,...,K''_p$ dans cette base, et donc telle que

$$H_1(V)\simeq \mathbb{Z}^{2p}/M(\mathbb{Z}^{2p}).$$

Poincaré distingue trois cas.

• Si $|\det(M)|>1$, $H_1(V)$ est fini mais non trivial

les « coefficients de torsion » (cf. p. 363) ne sont pas égaux à $1$.

Par contre, $M$ est inversible sur $\mathbb{Q}$ donc $H_1(V,\mathbb{Q}) \simeq \mathbb{Q}^{2p}/M(\mathbb{Q}^{2p})$ est trivial :

Le nombre de Betti relatif aux homologies par division est donc égal à $1$.

• Si $|\det(M)|=1$, $M$ est inversible sur $\mathbb{Z}$, donc $H_1(V)$ est trivial.

Le nombre de Betti et les coefficients de torsion sont donc les mêmes que pour une variété simplement connexe. Cela ne veut pas dire comme nous le verrons bientôt, que la variété $V$ soit simplement connexe.

• Enfin si $\det(M)=0$, $H_1(V)$ a une partie libre, de dimension $2p- rg(M)$.

Ce qui intéresse Poincaré, c’est le cas où $W$ est une sphère d’homologie, donc le cas où le déterminant de la matrice $M$

est égal à $\pm 1$. Dans ce cas, on peut se demander si la variété est simplement connexe, puisqu’elle a même nombre de Betti et mêmes coefficients de torsion que les variétés simplement connexes. Nous allons voir, et c’est là le but principal de ce travail, qu’il n’en est pas toujours ainsi, et pour cela nous nous bornerons à donner un exemple.

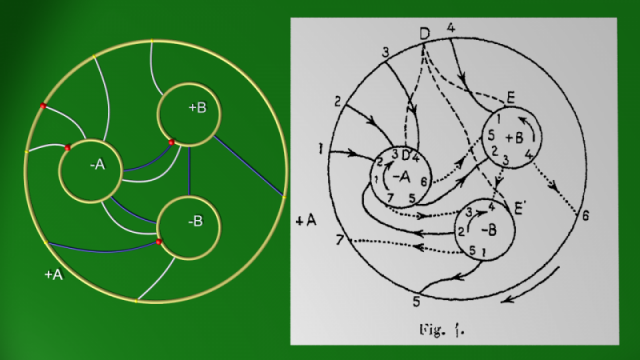
Le diagramme de Heegaard de Poincaré

L’exemple de Poincaré est une variété $V$ comme celles étudiées jusqu’ici, avec $p=2$.
Elle admettra donc un scindement de Heegaard en deux corps en anse $V',V''$ de genre deux. Poincaré caractérise la variété $V$ par ses deux paires de courbes fermées $K_1', K'_2$ et $K_1'',K''_2$ tracées sur la surface $W=\partial V'=\partial V''$, qui seront des familles maximales de courbes de compression pour les corps en anses $V'$ et $V''$ respectivement.

Pour $K_1'$, $K'_2$, Poincaré prend les « cycles fondamentaux » $C_1$ et $C_3$ définis dans le §3. Il représente alors sa surface par un « polygone fuchsien de la troisième famille » en la découpant le long de ces deux courbes, et trace $K_1''$ et $K''_2$ sur la figure obtenue (un disque à $3$ trous, ou une sphère à $4$ trous) :

Sur notre diagramme simplifié (à gauche), $K''_1$ et $K''_2$ correspondent aux courbes blanche et bleue respectivement. Nul besoin de les orienter pour décrire la variété $V$ (cela sera utile en revanche pour les décomposer en terme des lacets fondamentaux). Les cercles $\pm A$ correspondent au « cycle fondamental » $K'_1=C_1$ et les cercles $\pm B$ au « cycle fondamental » $K'_2=C_3$. La manière dont les cercles $+A$ et $-A$ (resp. $+B$ et $-B$) (et donc les extrémités des arcs bleus et blancs) doivent être identifiés est bien déterminée, sur la figure simplifiée, par les marques rouges, qui doivent elles-mêmes être identifiées.

Les paires $(K_1',K'_2)$ et $(K_1'',K''_2)$ choisies par Poincaré sont bien des paires de lacets simples disjoints, mais avant d’aller plus loin, il faut s’assurer qu’elles définissent bien un diagramme de Heegaard, c’est-à-dire qu’elles peuvent effectivement être des paires de courbes de compression d’une variété possédant un scindement de Heegaard de genre $2$. Pour cela, il faut et il suffit que la surface $W$ découpée le long des courbes de l’une ou l’autre de ces paires soit une sphère trouée. C’est immédiat pour la première paire (c’est « comme ça » qu’ont été définis les lacets $C_{2p+1}$). Poincaré montre ensuite (de On s’en rendra mieux compte à $K_1',K_2'$) qu’il existe un homéomorphisme de $W$ qui intervertit les paires $(K_1',K'_2)$ et $(K_1'',K''_2)$, ce qui montre que la deuxième paire a aussi la propriété voulue. Mais il suffirait en fait simplement d’utiliser la décomposition, déterminée juste après, de ces lacets en termes des lacets fondamentaux pour vérifier qu’ils sont indépendants en homologie.

Reste une question bien mystérieuse : comment diable Poincaré a-t-il choisi ses courbes ? Par essais et erreurs, un peu au hasard ? Combien de tentatives a-t-il faites avant de tomber sur « les bonnes » courbes ? Tout cela est un peu frustrant d’autant plus qu’on est surpris qu’il n’ait pas pensé à un lien avec le dodécaèdre. Dans le premier mémoire, il pense au cube, à l’octaèdre, dont il identifie les faces par paires, mais il ne va pas jusqu’au dodécaèdre, dont il était pourtant évidemment familier. Nous réparons cela dans une longue rubrique qui propose six différentes manières de voir ce petit bijou qu’est la sphère d’homologie de Poincaré.

Calcul du $\pi_1$ et du $H_1$

Poincaré applique alors son « algorithme » du §4 pour déterminer, à partir de leurs intersections successives avec les lacets $C_1,...,C_4$ (comme définis au début du §4, avant qu’on ne les fasse passer par un même point...), la décomposition de $K''_1$ et $K''_2$, à homotopie (libre) près en termes de $C_1,...,C_4$.

Nous faisons cadeau au lecteur de cet exercice fastidieux [1], au terme duquel on obtient (en notation multiplicative) :

$$K''_1 = C_2^3C_1C_2C_3^{-1}C_4C_2^{-1}C_4^{-1}C_3^{-1}C_4^2$$

et

$$K_2'' = C_4^{-2}C_3C_2^{-1}C_4^{-1}C_3^{-1}C_4^2C_2^{-1}.$$

Notons qu’en homologie, en identifiant $H_1(W)$ à $\mathbb{Z}^4$, on obtient

$$K''_1 \sim (1,3,-2,2)\quad \text{et} \quad K''_2 \sim (0,-2,0,-1),$$

qui forment bien, comme annoncé, une famille libre.

Mieux, la matrice $M$ des coordonnées de $K_1'$, $K'_2$, $K_1''$, $K''_2$ dans la base fondamentale est

$$\begin{pmatrix} 1&0&1&0\\ 0&0&3&-2\\ 0&1&-2&0\\ 0&0&2&-1 \end{pmatrix},$$

dont le déterminant vaut $-1$, donc d’après ce qui précède, $H_1(V)$ est trivial.

Et cependant $V$ n’est pas simplement connexe ; car son groupe fondamental ne se réduit pas à la substitution identique

En effet,

$$\pi_1(W)\simeq \langle C_1,C_2,C_3,C_4\; |\; [C_1,C_2][C_3,C_4]\rangle,$$

et vues les expressions de $K_1'$, $K'_2$, $K_1''$, $K''_2$, $\pi_1(V)$ a pour présentation

$$\langle C_1,C_2,C_3,C_4\; |\; [C_1,C_2][C_3,C_4], C_1, C_3, C_2^3C_1C_2C_3^{-1}C_4C_2^{-1}C_4^{-1}C_3^{-1}C_4^2,\\\hspace{7cm}C_4^{-2}C_3C_2^{-1}C_4^{-1}C_3^{-1}C_4^2C_2^{-1}\rangle $$

qui se simplifie immédiatement (en éliminant $C_1$ et $C_3$) en :

$$\langle C_2,C_4\; |\; C_2^4C_4C_2^{-1}C_4,C_4^{-2}C_2^{-1}C_4C_2^{-1}\rangle.$$

Il s’agit de vérifier que ce groupe n’est pas trivial. Pour cela, Poincaré considère son quotient

$$\langle C_2,C_4\; |\; C_2^4\mathbf{C_4C_2^{-1}C_4},C_4^{-2}\mathbf{C_2^{-1}C_4C_2^{-1}},(C_2^{-1}C_4)^2\rangle$$

qui, en remplaçant les parties en gras des deux premières relations par $C_2$ et $C_4^{-1}$ respectivement grâce à la dernière relation, est isomorphe à

$$\langle C_2,C_4\; |\; C_2^5,C_4^{-3},(C_2^{-1}C_4)^2\rangle.$$

Poincaré reconnaît là une présentation du groupe des rotations de l’icosaèdre, qui est clairement non trivial, donc $\pi_1(V)$, qui l’admet pour quotient [2], est également non trivial.

Concluons avec les mots de Poincaré :

Il resterait une question à traiter :

Est-il possible que le groupe fondamental de $V$ se réduise à la substitution identique, et que pourtant $V$ ne soit pas simplement connexe ?

[...]

Mais cette question nous entraînerait trop loin.

Il ne croyait probablement pas si bien dire... Cette question, connue aujourd’hui sous le nom de Conjecture de Poincaré [3], n’a été résolue qu’en 2004 par G. Perelman. Toutefois, dans sa formulation (les [...] que nous avons enlevés), Poincaré semble se restreindre au cas d’une variété de genre de Heegaard égal à 2. [4] Or d’après Birman et Hilden [5] toute 3-variété de genre de Heegaard égal à 2 peut être obtenue comme revêtement de degré 2 de $\mathbb{S}^3$ ramifié au-dessus d’un noeud. Et, dans ce cas, la conjecture de Poincaré est démontrée dès 1978 comme conséquence de la conjecture de Smith [6]. L’approche de Poincaré semble avoir été combinatoire. On a d’ailleurs longtemps pensé que jongler avec la présentation du groupe fondamental déduite d’une décomposition de Heegaard permettrait de résoudre la conjecture de Poincaré, en déterminant à quelles conditions le groupe est trivial. En 1965, Stallings écrit d’ailleurs un article resté célèbre :

« How not to prove the Poincaré conjecture »

qui contenait le commentaire suivant « I have committed the sin of falsely proving Poincaré’s Conjecture. But that was in another country ; and besides, until now, no one has known about it. »

On ne compte plus le nombre d’erreurs engendrées par la conjecture de Poincaré. En dimension $n \geq 5$, la méthode originale de Poincaré — la théorie de Morse — a effectivement permit à Smale [7] de démontrer que toute sphère d’homotopie de dimension $n$ est homéomorphe à la sphère de dimension $n$. [8] En dimension $3$ c’est finalement l’étude analytique de l’espace (de dimension infini) constitué de toutes les métriques riemanniennes sur une 3-variété donnée qui a permis à Perelman d’emporter le morceau.