Commentaires sur le §4 du Cinquième Complément

Nous structurons notre commentaire selon le découpage suivant du texte :

1. de Mais avant d’aborder cette question à équivalence propre, retour sur les différents types d’équivalence (homotopie, homotopie libre, homologie entière, homologie rationnelle)
2. de On peut se placer à ces cycles ne se couperont pas ; traduction au niveau du revêtement universel du fait, pour des lacets, d’être homotopes, librement homotopes, simples, homotopes à des lacets simples, disjoints... Ici, on voit la surface comme quotient du disque unité (le revêtement universel), par un groupe fuchsien (auquel s’identifie le groupe fondamental), un domaine fondamental ayant été obtenu en découpant la surface le long des $2p$ lacets fondamentaux et en identifiant le $4p$-gone obtenu à un polygone fuchsien.
3. de Plaçons-nous maintenant à $- C_4, + C_3$ ; on peut aussi voir la surface simplement comme le $4p$-gone avec ses côtés identifiés deux-à-deux, et donc tout lacet sur la surface comme un ensemble d’arcs dans ce polygone, déterminé par la liste des côtés que ces arcs rencontrent successivement, côtés qui correspondent aux "coupures" $C_1,...,C_{2p}$, et eux-mêmes notés $\pm C_1,...,\pm C_{2p}$ (selon qu’ils correspondent au côté « droit » ou « gauche » de la coupure). Il y a alors un algorithme simple qui à une telle liste associe, par « dualité », une combinaison des lacets fondamentaux à laquelle le lacet est librement homotope. Réciproquement, un mot en les lacets fondamentaux peut être traduit de façon systématique en une liste de côtés, correspondant aux intersections successives d’un lacet décrit par ce mot avec les côtés du polygone.
4. de Deux arcs $A_iB_i$ et $A_kB_k$ à $C_3+C_1$ ; l’intérêt de la liste est qu’on y lit plus directement si un lacet s’auto-intersecte ou pas, ce que l’on peut ensuite traduire, grâce à la correspondance ci-dessus, en condition pour qu’une combinaison de lacets fondamentaux soit homotope à un lacet simple. [1]
5. de Mais pour ce qui va suivre à la fin du paragraphe ; traduction de ce qui précède dans le cas où on ne regarde pas notre surface comme un $4p$-gone aux côtés identifiés deux à deux, mais comme une sphère à $2p$ trous dont on identifie les composantes de bord deux à deux. En effet, c’est dans ce cadre que Poincaré va définir sa sphère d’homologie dans le §6.

Nous n’avons pas grand-chose à ajouter sur les points 1 [2] et 2 [3].

Algorithmes de traduction

Dans le §3, Poincaré a défini une famille de $2p$ cycles fondamentaux qui découpent sa surface considérée en un $4p$-gone (voir nos commentaires). Tout lacet sur la surface correspond (à une petite déformation près) à une suite d’arcs transverses au bord dans ce $4p$-gone, l’extrémité finale d’un arc étant identifiée (dans la surface obtenue en recollant deux à deux les côtés du $4p$-gone) à l’extrémité initiale de l’arc suivant. Il correspond ainsi à chaque lacet la liste (à permutation cyclique près) des côtés du polygone qu’il rencontre, ceux-ci étant nommés $C_1, C_1',...,C_{2p},C'_{2p}$ (où les côtés $C_i$ et $C_i'$ correspondent au même cycle dans la surface) comme dans l’animation ci-dessous (chez Poincaré, ils sont nommés $\pm C_1,...,\pm C_{2p}$). Dans cette animation, nous avons tracé le lacet correspondant à la « liste »

$$C_1,C_2,C_2',C_3,C_3',C_1',$$

c’est à dire à l’union de trois arcs reliant respectivement $C_1$ à $C_2$, $C'_2$ à $C_3$ et $C'_3$ à $C_1'$, arcs que nous noterons ici simplement $C_1C_2$, $C'_2C_3$ et $C'_3C_1'$. Poincaré explique, sous forme d’un tableau de correspondances, un algorithme pour traduire une telle liste ou suite d’arcs en un mot en les lacets fondamentaux, auquel notre lacet soit librement homotope. L’animation suivante présente cet algorithme.

On commence par homotoper le chemin initial, donné comme une union d’arcs, en un chemin dont tous les arcs passent par le centre de l’octogone. Plutôt que de prendre le point base sur le côté $C_1$, on le prend au milieu de l’arc joignant $C_3'$ à $C_1'$. Notre nouveau chemin se décompose alors naturellement comme une union d’arcs, chacun de ces arcs joignant un côté $C_k$ au côté conjugué $C_k'$, ou l’inverse (sur l’exemple, on a d’abord un arc joignant $C_1$ à $C_1'$, puis un arc joignant $C_2'$ à $C_2$, et enfin un arc joignant $C_3'$ à $C_3$). Or, par construction des cycles fondamentaux, un tel arc est homotope, parmi les arcs joignant un point du côté $C_k$ au point qui lui est identifié sur le côté $C_k'$, à un côté du $4g$-gone [4]. Sur la surface, ceci revient à décomposer notre lacet initial, après changement du point base, comme produit de lacets librement homotopes à des cycles fondamentaux ou leurs inverses. Sur l’exemple, on a écrit le lacet de départ comme produit des cycles fondamentaux $C_2$, puis $C_1$, puis $C_4^{-1}$, à homotopie libre près.

On voit que la $i$ème lettre du mot ainsi formé (ainsi que son exposant) est uniquement déterminée par le côté de départ du $i$ème arc (ou de façon équivalente le côté d’arrivée du $(i-1)$ième) selon la correspondance du tableau suivant, où $N$ désigne le point de départ du $i$ème arc, et où la première colonne donne la $i$ème lettre du mot :

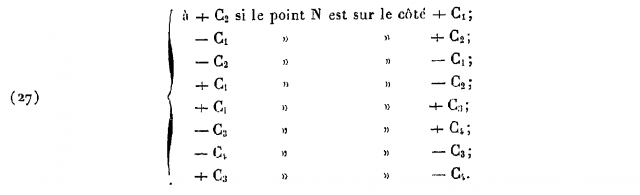
En notations modernes, les $-C_i$ de la première colonne deviennent $C_i^{-1}$. Quant aux $-C_i$ de la deuxième colonne, ils correspondent à nos $C_i'$.

Réciproquement, étant donné un mot en les $C_i$ et leurs inverses, il est facile de tracer dans l’octogone un lacet issu du centre, transverse au bord, ayant cette décomposition en termes des cycles fondamentaux (plus précisément de cycles librement homotopes à ceux-ci et ayant pour point base le centre de l’octogone).

Pour obtenir un tel lacet librement homotope à $C_i^{\pm1}$ simplement, il suffit de considérer, parmi les deux côtés $C_i$ et $C_i'$, celui qui est entouré par deux autres côtés conjugués de l’octogone $C_k$ et $C_k'$ (il n’y en a qu’un, $C_i$ si $i$ est pair, $C_i'$ si $i$ est impair), et de tracer un lacet allant du centre à $C_k$ et du point conjugué sur $C_k'$ au centre, ou inversement.

Pour un mot plus compliqué, il suffit d’appliquer ce qui précède lettre par lettre. En changeant de point base (en plaçant celui-ci à mi-chemin du premier lacet de la décomposition, sur un côté donc), on peut alors voir ce lacet comme une suite d’arcs allant du bord au bord, le point de départ du $i$ème arc étant déterminé par la $i$ème lettre du mot, et son point d’arrivée par la $(i+1)$ième lettre. Ainsi chaque arc est déterminé par ce que Poincaré appelle une séquence du mot, sous-mot composé de deux lettres successives, selon la correspondance suivante :

A chaque séquence correspondra un arc $A_i B_i$ ; le point $A_i$ se trouvera sur le côté

$$ + C_1, + C_2 , -C_1, -C_2 , + C_3 , + C_4, - C_3, - C_4$$

si le premier terme de la séquence est respectivement

$$ + C_2, -C_1, -C_2, +C_1, + C_4, - C_3, - C_4, + C_3, $$

et le point $B_i$ se trouvera sur le côté

$$ - C_1, - C_2, + C_1, + C_2, - C_3, -C_4, + C_3, + C_4$$

si le second terme de la séquence est respectivement

$$ + C_2, -C_1, -C_2, +C_1, + C_4, - C_3, - C_4, + C_3. $$

L’animation suivante applique cet algorithme au mot $C_1C_2^{-1}C_3$, dont les séquences sont $C_1C_2^{-1}$, $C_2^{-1}C_3$ et $C_3C_1$, séquence formée de la dernière lettre et de la première.

Lacets simples et séquences incompatibles

Deux « séquences » d’un mot correspondent donc à deux arcs du lacet associé. Or Poincaré fait remarquer qu’il est facile de déterminer si deux arcs se croisent ou non selon la répartition de leurs extrémités sur le bord de l’octogone, i.e. simplement de la répartition des côtés auxquels appartiennent ces extrémités. Ainsi dans le cas « facile » où ces quatre côtés sont distincts : deux arcs

$$C_{i_1}^{\epsilon_1}C_{i_2}^{\epsilon_2} \mbox{ et } C_{i_3}^{\epsilon_3} C_{i_4}^{\epsilon_4} \ (\mbox{avec } \epsilon_i=\emptyset \mbox{ ou } ' )$$

s’intersectent si et seulement si les côtés correspondants du $4p$-gone sont « enchâssés », au sens où, en parcourant le bord du polygone (dans le sens direct ou indirect) on les rencontre dans l’ordre

$$\cdots C_{i_1}^{\epsilon_1} \cdots C_{i_3}^{\epsilon_3} \cdots C_{i_2}^{\epsilon_2} \cdots C_{i_4}^{\epsilon_4} \cdots$$

Dans le cas où les deux arcs rencontrent un même côté, c’est moins évident mais Poincaré explique ici que cela ne dépend encore que de la répartition des côtés auxquels appartiennent ces extrémités.

Les deux séquences sont dites compatibles si les arcs correspondant ne se croisent pas et incompatibles dans le cas contraire. D’après l’algorithme ci-dessus la compatibilité ou l’incompatibilité de deux séquences d’un mot s’exprime en termes des lettres du mot. Tout l’intérêt est maintenant qu’un mot dont toutes les séquences sont compatibles peut évidemment être représenté par un lacet simple.

Réciproquement, Poincaré affirme qu’un mot qui possède deux séquences incompatibles
ne peut pas être représenté par un lacet simple à moins que l’on puisse faire disparaître ces séquences par la relation $\Pi[C_{2p-1},C_{2p}]=1$.

Quelques commentaires supplémentaires

Considérons plus généralement une surface compacte orientable $S$, avec $\chi (S) <0$, que l’on représente comme quotient $\Gamma \backslash U$ où $U \subset \mathbb{D}$ est le revêtement universel de $S$ et où $\mathbb{D}$ est le disque unité muni de sa métrique de Poincaré (métrique hyperbolique) et $\Gamma$ est un sous-groupe discret d’isométries hyperboliques.

Poincaré a donc commencé par montrer qu’une classe d’homotopie libre de lacet fermé dans $S$ contient un unique représentant géodésique et que la classe d’homotopie libre contient un représentant simple si et seulement si l’unique représentant géodésique est simple.

Un système de générateurs de $\Gamma$ étant fixé on peut considérer un mot en ces générateurs qui représente la classe d’homotopie libre considérée. Lorsque $\partial S \neq \emptyset$ le groupe $\Gamma$ est libre et toute classe de conjugaison possède un unique représentant de longueur minimale en les générateurs ; celui-ci est obtenu par réduction cyclique d’un mot quelconque représentant un élément quelconque de cette classe de conjugaison. Dans ce cas on peut appliquer l’algorithme de Poincaré à ce mot : la classe d’homotopie libre contient un représentant simple si et seulement si les séquences de ce mot sont deux à deux compatibles.

Par contre si $\partial S = \emptyset$ il n’y a pas unicité du mot le plus court dans une classe de conjugaison. Toutefois si $m \in \Gamma$ est un mot de longueur minimale dans sa classe de conjugaison qui de plus ne contient (cycliquement) aucun sous mot qui soit la moitié d’un relateur (c’est-à-dire un sous mot (cyclique) de $\Pi[C_{2p-1},C_{2p}]$ dans les notations ci-dessus) alors le problème de décider si $m$ est simple se ramène à considérer le problème sur la surface $S$ privée d’un disque de sorte que l’on peut tout simplement voir $\Gamma$ comme un groupe libre. On peut alors appliquer l’algorithme proposé par Poincaré. Il resterait à détailler les cas exceptionnels où $m$ contient un demi-relateur...

Pour conclure, notons que la recherche de ce type d’algorithme a une riche histoire depuis Poincaré, on pourra par exemple consulter [5].

$$ $$

Poincaré illustre la puissance de ces réflexions en affirmant :

L’application de ces règles nous apprend, par exemple, que de toutes les combinaisons des cycles impairs $C_1$ et $C_3$, les seules qui soient équivalentes à des cycles non bouclés sont les suivantes :

$$C_1, C_3, C_1 + C_3, C_3 + C_1.$$

Faisons l’exercice.

Considérons un lacet se décomposant en $C_1$, $C_3$ et leurs inverses. D’après l’algorithme ci-dessus, il est librement homotope à un lacet dont la représentation dans l’octogone est un ensemble d’arcs ne rencontrant que les côtés $C_2$, $C_2'$, $C_4$ et $C_4'$, i.e. à un lacet qui, dans la surface, ne recontre pas les « coupures » $C_1$ et $C_3$. Le lacet est donc librement homotope à une courbe simple fermée tracée sur un « pantalon » dont les « tours de jambes » représentent les classes d’homotopie libre $C_1$, $C_3$ et $C_1+C_3$ (qui est librement homotope à $C_3+C_1$). Il reste à vérifier que (exception faite des lacets opposés que Poincaré oublie) toute autre courbe fermée est bouclée sur un pantalon. Cela peut se déduire facilement en appliquant l’algorithme de Poincaré à un choix de structure hyperbolique sur le pantalon.

Remarquons qu’il n’est pas évident d’obtenir ce résultat en appliquant à la lettre la méthode de Poincaré (dans la preuve au dessus on se ramène par exemple au cas d’un pantalon), et l’on reste un peu perplexe quant à la façon dont il a pu s’en servir pour choisir ses courbes (autrement plus complexes !) dans le §6...

Algorithmes analogues dans le cas où la surface est représentée par un polygone « de la troisième famille »

On se replace dans le cadre « sphère trouée » et cette fois un lacet n’est plus décrit par une liste d’intersections avec des côtés d’un polygone, mais par une liste d’intersections avec les « lèvres » et avec des arcs les reliant. Cette liste aussi se traduit facilement en mot en les générateurs. Et réciproquement. On obtient un algorithme analogue que nous ne détaillons pas. C’est toutefois plus spécifiquement cet algorithme que Poincaré utilisera dans le §6.