§6 du cinquième complément

Considérons maintenant une variété $V$ à trois dimensions dont le squelette se réduira à un segment de droite le long duquel la variable $t$ variera de $0$ à $1$. Le système $W(t)$ se composera d’une variété unique ; cette variété sera une surface fermée bilatère, qui se réduira à un point pour $t=0$ et pour $t=1$, et dont l’ordre de connexion ira en croissant de $t=0$ à $t=\frac{1}{2}$ et en décroissant de $t=\frac{1}{2}$ à $t=1$. Notre variété $V$ est donc fermée.

Nous aurons $2p$ valeurs remarquables de $t$, satisfaisant aux inégalités

$$0< t_1< t_2< \ldots t_p< \frac{1}{2}< t'_p< \ldots< t'_2< t'_1<1, $$

de telle façon que, quand $t$ passera de la valeur $t_q - \epsilon$ à la valeur $t_q + \epsilon$, la surface $W(t)$ passera de la connexion $2q-1$ à la connexion $2q +1$, et que quand $t$ passera de la valeur $t'_q - \epsilon$ à la valeur $t'_q + \epsilon$, la surface $W(t)$ passera de la connexion $2q+1$ à la connexion $2q-1$.

La variété $V$ pourra se décomposer en deux autres $V'$ et $V{''}$ correspondant, la première aux valeurs de $t$ comprises entre $0$ et $\frac{1}{2}$, la seconde aux valeurs de $t$ comprises entre $\frac{1}{2}$ et $1$. Chacune des ces deux variétés partielles répond aux conditions du paragraphe précédent ; elle est donc développable et c’est la variété $V$ formée par leur réunion qu’il s’agit maintenant d’étudier.

Ces deux variétés $V'$ et $V''$ ont pour frontière commune la surface $W\left(\frac{1}{2}\right)$ que j’appellerai $W$ et qui est $2p+1$ fois connexe.

Sur cette surface, je puis tracer d’une part les $p$ cycles

$$K'_1, K'_2, \ldots, K'_p$$

définis par rapport à la variété $V'$ comme l’ont été dans le paragraphe précédent les cycles $K_1, K_2, \ldots, K_p$ par rapport à la variété $V$ du paragraphe précédent.

Ces $p$ cycles ne sont pas bouclés et ne se coupent pas. De plus, on a les équivalences

$$ \tag{1} K'_1\equiv K'_2 \equiv \ldots \equiv K'_p \equiv 0 \quad(\textrm{mod}\, V'). $$

D’autre part, sur cette même surface $W$ je puis tracer les $p$ cycles

$$K''_1, K''_2, \ldots, K''_p$$

définis par rapport à $V''$ comme l’ont été au paragraphe précédent les cycles $K_q$ par rapport à la variété $V$ du paragraphe précédent.

Les $p$ cycles $K''$ ne sont pas bouclés et ne se coupent pas ; et l’on a les équivalences

$$ \tag{2} K''_1\equiv K''_2 \equiv \ldots \equiv K''_p \equiv 0 \quad(\textrm{mod}\,V''). $$

Les cycles $K'$ seront alors les cycles principaux de $V'$ et les cycles $K''$ ceux de $V''$.

Considérons maintenant un cycle $C$ quelconque intérieur à $V$ ; si $M$ est un point quelconque de ce cycle, nous pouvons envisager le point correspondant $N$ du squelette. Quand le point $M$ décrira le cycle tout entier, le point $N$ restera sur la droite $0$ $1$ qui constitue le squelette et exécutera sur cette droite une série de mouvements oscillatoires à la suite desquels il reviendra à son point de départ.

Soient $A$ et $B$ les deux positions extrêmes du point $N$ dans cette oscillation. Supposons que le point $A$ soit compris entre $t_q$ et $t_{q+1}$ et que le point $N$ partant de la valeur $t_{q+1}- \epsilon$ décroisse jusqu’à $A$ pour revenir à la valeur $t_{q+1}- \epsilon$. Soit $H$ l’arc correspondant du cycle $C$ ; soit $M$ un point de cet arc $H$, il appartiendra à la surface $W(t)$, $t$ étant compris entre $A$ et $t_{q+1}- \epsilon$. Nous savons que la surface $W(t)$ reste homéomorphe à elle-même quand $t$ varie entre $t_{q+1} - \epsilon$ à $t_q + \epsilon$ et, par conséquent, quand $t$ varie entre $t_{q+1} - \epsilon$ à $A$, puisque $A$ est plus grand que $t_q$. Donc $W(t)$ est homéomorphe à $W(t_{q+1} - \epsilon)$. Soit $M'$ le point de $W(t_{q+1} - \epsilon)$ qui correspond à $M$. Quand le point $M$ décrira l’arc $H$, le point $M'$ décrira l’arc $H'$ situé tout entier sur $W(t_{q+1} - \epsilon)$. Je dis qu’on a l’équivalence

$$H \equiv H' \quad(\textrm{mod}\,V).$$

En effet, considérons les différentes surfaces $W(t)$, où $t$ a une valeur intermédiaire entre celle qui correspond au point $M$ et la valeur $t_{q+1}- \epsilon$ qui correspond à $M'$. Considérons sur chacune de ces différentes surfaces qui sont toutes homéomorphes entre elles, le point qui correspond à $M$. Ce point engendrera une ligne $L$ dont les extrémités seront $M$ et $M'$ ; quand le point $M$ décrira l’arc $H$, cette ligne $L$ engendrera une aire simplement connexe qui aura pour frontière complète les deux arcs $H$ et $H'$ ; ce qui démontre l’équivalence annoncée.

Considérons maintenant les deux surfaces $W(t_{q+1} - \epsilon)$ et $W(t_{q+1} + \epsilon)$ ; sur la première nous avons l’arc $H'$ dont les deux extrémités $D$ et $E$ appartiennent à l’arc $H$ et, par conséquent, au cycle $C$ ; sur la seconde nous avons les deux points $D'$ et $E'$, infiniment voisins de $D$ et de $E$ et qui appartiennent aussi à $C$, de telle façon que $DD'$ et $EE'$ soient deux arcs infiniment petits de ce cycle $C$. Nous pouvons tracer sur la surface $W(t_{q+1} - \epsilon)$ un arc $H''$ allant de $D'$ en $E'$ et infiniment peu différent de $H'$. Ce dernier point mérite quelque attention. Les deux surfaces $W(t_{q+1} - \epsilon)$ et $W(t_{q+1} + \epsilon)$ n’ont pas le même ordre de connexion ; il pourrait donc se faire, bien que ces deux surfaces diffèrent très peu l’une de l’autre, qu’on ne puisse pas tracer sur l’une un trait continu très peu différent d’un trait continu tracé sur l’autre. Si sur celle dont la connexion est plus élevée, on avait un trait continu $L$ passant près du point singulier et coupant le cycle qui se réduit à un point pour $t=t_{q+1}$, on ne pourrait tracer sur l’autre un trait continu très peu différent de $L$. Par exemple, considérons trois surfaces très peu différentes l’une de l’autre ; la première sera un hyperboloïde à une nappe, la seconde un cône, la troisième un hyperboloïde à deux nappes, le cycle qui se réduit à un point est l’ellipse de gorge de l’hyperboloïde à une nappe. Une génératrice rectiligne de l’hyperboloïde à une nappe coupera cette ellipse et il sera impossible de tracer sur la troisième surface un trait continu très peu différent de cette génératrice. Mais ici cette difficulté n’est pas à craindre puisque c’est $W(t_{q+1} + \epsilon)$ qui a la connexion la plus élevée. Notre arc $H''$ existera toujours et l’on aura

$$H' \equiv D'D+ H +E'E\quad(\textrm{mod}\,V);$$

alors posons

$$C=C_1 + D'D + H+ E'E$$

de telle façon que notre cycle $C$ se décompose en deux arcs, le premier $C_1$ et le second $D'D + H+ E'E$, ayant tous deux pour extrémités $D'$ et $E'$. Nous aurons

$$C \equiv C_1 + H''\quad(\textrm{mod}\,V).$$

Nous avons ainsi remplacé le cycle $C$ par un autre cycle équivalent $C_1 + H''$ qui jouit des mêmes propriétés, mais qui en diffère parce que le point représentatif $N$ au lieu d’aller jusqu’en $A$ dans ses oscillations ne dépasse plus $t_{q+1} + \epsilon$.

Supposons d’abord que la valeur $t=\frac{1}{2}$ soit comprise entre les points $A$ et $B$ entre lesquels oscille le point $N$, et que le point $A$ soit compris entre $t_q$ et $t_{q+1}$, et le point $B$ entre $t'_q$ et $t'_{q+1}$. Nous pouvons, par le procédé que je viens d’exposer, remplacer le cycle $C$ par un autre où le point $N$ oscillera entre $B$ et le point $t_{q+1} + \epsilon$, ce dernier point n’étant plus compris comme le point $A$ entre $t_q$ et $t_{q+1}$, mais bien entre $t_{q+1}$ et $t_{q+2}$. Nous pouvons, en d’autres termes, ramener le point $A$ entre $t_{q+1}$ et $t_{q+2}$ ; en continuant nous le ramènerons entre $t_{q+2}$ et $t_{q+3}$, etc., puis enfin entre $t_p$ et $\frac{1}{2}$. En opérant sur $B$ et $V''$ comme nous l’avons fait sur $A$ et $V'$, nous ramènerons de même le point $B$ entre $\frac{1}{2}$ et $t'_p$.

En résumé, nous aurons remplacé le cycle $C$ par un autre cycle équivalent $C'$, tel que le point $N$ reste toujours compris entre $t_p$ et $t'_p$. Mais quand $t$ est compris entre $t_p$ $t'_p$ la surface $W(t)$ reste homéomorphe à elle-même et à $W(\frac{1}{2})$ ou $W$. Soit donc $M$ un point quelconque du cycle $C'$ appartenant à $W(t)$ et $M'$ le point correspondant de $W$. Quand le point $M$ décrira le cycle $C'$, le point $M'$ décrira un cycle $C''$ situé sur $W$ et l’on aura

$$C' \equiv C''$$

par un raisonnement tout pareil à celui qui nous a montré que $H \equiv H'$. On aura donc

$$C \equiv C'\quad(\textrm{mod}\,V).$$

Si les points $A$ et $B$ n’étaient pas situés d’une part et d’autre de $\frac{1}{2}$, si par exemple $t$ restait $< \frac{1}{2}$ pour le cycle $C$ tout entier, on remplacerait le cycle $C$ par le cycle équivalent

$$C + \alpha - \alpha,$$

où l’arc $\alpha$, qui est parcouru dans le sens direct, puis dans le sens inverse, s’étendrait depuis le point final du cycle $C$, jusqu’à un point quelconque de $V$ tel que $t > \frac{1}{2}$. On serait ainsi ramené au cas précédent. Nous sommes donc conduits à la conclusion générale suivante :

Tout cycle de $V$ est équivalent à un cycle de $W$.

Maintenant entre les cycles de $W$ nous avons les équivalences (1) et (2)

$$K'_i \equiv 0\quad(\textrm{mod}\,V'),~~~~K''_i \equiv 0\quad(\textrm{mod}\,V'')$$

et nous aurons a fortiori

$$ \tag{3} K'_i\equiv K''_i \equiv 0\quad(\textrm{mod}\,V). $$

Je dis maintenant qu’il n’y en aura pas d’autres.

Si, en effet, il y a une équivalence

$$K \equiv 0\quad(\textrm{mod}\,V),$$

$K$ étant un cycle de $W$, cela veut dire qu’il existe dans $V$ une aire simplement connexe $A$ dont la frontière est formée par le cycle $K$. Cela posé, nous distinguerons dans $A$ les points qui appartiennent à $V'$ et qui formeront l’aire $A'$, laquelle pourra ne pas être d’un seul tenant, et les points qui appartiennent à $V''$ et qui formeront l’aire $A''$. Si l’aire $A'$ n’est pas d’un seul tenant, elle sera formée de plusieurs aires séparées $A'_1, A'_2, \ldots ,$ dont chacune sera d’un seul tenant. De même pour $A''$. Si nous considérons l’une de ces aires partielles $A'_1$ par exemple, il pourra se faire qu’elle ne soit pas simplement connexe. Supposons, par exemple, qu’elle soit triplement connexe et limitée, par conséquent, extérieurement par une courbe fermée $L$, et intérieurement par deux courbes fermées $L'$ et $L''$ (les mots extérieurement et intérieurement doivent s’entendre par rapport à l’aire totale $A$). Joignons un point de $L$ à un point de $L'$ par une coupure $P'$ et, de même, un point de $L$ à un point de $L''$ par une coupure $P''$ ; ces deux coupures $P'$ et $P''$ seront des arcs de courbe situés sur $A'_1$ et rendront $A'_1$ simplement connexe. Soit $B'_1$ l’aire simplement connexe ainsi obtenue ; et soit $D'_1$ son contour qui sera formé des courbes fermées $L$, $L'$ et $L''$ et des deux coupures parcourues une fois dans le sens direct et une fois dans le sens inverse. L’aire $B'_1$ fera tout entière partie de $V'$ et l’on aura

$$D'_1 \equiv 0\quad(\textrm{mod}\,V').$$

On opérera de même pour les aires $A'_2, \ldots$ et l’on obtiendra une série d’équivalences

$$D'_2 \equiv \ldots \equiv 0\quad(\textrm{mod}\,V').$$

On opérera de même pour les aires $A''_1, A''_2, \ldots,$ dont l’ensemble forme $A''$, ce qui donnera les équivalences

$$D''_1 \equiv D''_2 \equiv \ldots \equiv 0\quad(\textrm{mod}\,V'').$$

Comme l’aire $A$ est formée par la réunion des des aires $B'_1, B'_2, \ldots; B''_1, B''_2, \ldots;$ l’équivalence $K \equiv 0$ où $K$ est le contour de l’aire totale $A$ sera une conséquence des équivalences

$$D'_1 \equiv D'_2 \equiv \ldots \equiv 0\quad(\textrm{mod}\,V'),$$

$$ D''_1 \equiv D''_2 \equiv \ldots \equiv 0\quad(\textrm{mod}\,V''),$$

où $D'_1, D'_2, \ldots; D''_1, D''_2, \ldots$ sont les contours des aires partielles $B'_1, B'_2, \ldots; B''_1, B''_2, \ldots$.

Notre équivalence est donc une conséquence de diverses équivalences prises les unes par rapport à $V'$, les autres par rapport à $V''$. Or toutes les équivalences par rapport à $V'$ sont des conséquences des équivalences (1) d’après le paragraphe précédent. Toutes les équivalences par rapport à $V''$ sont des conséquences des équivalences (2). Donc notre équivalence est une conséquence des équivalences (1) et (2) ou, ce qui revient au même des équivalences (3).

C.Q.F.D.

Possédant ainsi toutes les équivalences possibles, il est aisé d’en déduire toutes les homologies sans division possibles ; il suffit d’intervertir l’ordre des termes dans les premiers membres de ces équivalences. Soient

$$C_1, C_2, \ldots, C_{2p}$$

les $2p$ cycles fondamentaux de la surface $W$.

Nous aurons des homologies de la forme

$$K'_i \sim m'_{i,1} C_1 + m'_{i,2}C_2 + \ldots + m'_{i,2p}C_{2p}\quad(\textrm{mod}\,W)$$

et de la forme

$$K''_i \sim m''_{i,1} C_1 + m''_{i,2}C_2 + \ldots + m''_{i,2p}C_{2p}\quad(\textrm{mod}\,W)$$

(les $m'$ et les $m''$ étant des entiers), de sorte que nous aurons les homologies suivantes déduites des équivalences (3) :

$$ \tag{4} \left \{\begin{array}{ll} m'_{i,1}C_1 + m'_{i,2}C_2 + \ldots +m'_{i,2p}C_{2p} \equiv 0 \\ m''_{i,1}C_1 + m''_{i,2}C_2 + \ldots +m''_{i,2p}C_{2p} \equiv 0 \end{array} \quad(\textrm{mod}\,V) \right. $$

et nous n’en aurons pas d’autres.

Discutons ces homologies ; formons le déterminant $\Delta$ des entiers $m'$ et $m''$.

Trois cas sont à distinguer :

1° On a

$$|\Delta | >1.$$

Donc $\Delta$ est un entier qui n’est égal ni à $0$, ni à +1, ni à -1 ; nous pouvons alors déduire des homologies (4) sans faire de division

$$\Delta C_i \sim 0~~(i=1,2, \ldots, 2p)$$

et en faisant une division

$$C_i \sim 0,$$

Le nombre de Betti relatif aux homologies par division est donc égal à $1$.

Mais on ne pourrait obtenir $C_i \sim 0$ sans faire de division, de sorte que les « coefficients de torsion » (cf. p. 363) ne sont pas égaux à $1$.

2° On a

$$|\Delta | =1;$$

on en déduit alors sans division

$$C_i \sim 0.$$

Dans ce cas, non seulement le nombre de Betti, mais les coefficients de torsion sont égaux à $1$.

Le nombre de Betti et les coefficients de torsion sont donc les mêmes que pour une variété simplement connexe. Cela ne veut pas dire comme nous le verrons bientôt, que la variété $V$ soit simplement connexe.

3° On a

$$|\Delta | =0.$$

Des homologies (4) nous ne pouvons plus alors déduire

$$C_i \sim 0,$$

même en faisant une division.

Le nombre de Betti est donc plus grand que $1$.

Il est égal à $2$, si le déterminant $\Delta$ s’annule, mais si tous ses mineurs du premier ordre ne s’annulent pas.

Il est égal à $k$, si le déterminant s’annule ainsi que tous ses mineurs des $k-2$ premiers ordres, mais si tous ses mineurs du $k-1^{e}$ ordre ne s’annulent pas.

Revenons au cas où $\Delta$ est égal à $\pm 1$. Dans ce cas, on peut se demander si la variété est simplement connexe, puisqu’elle a même nombre de Betti et mêmes coefficients de torsion que les variétés simplement connexes. Nous allons voir, et c’est là le but principal de ce travail, qu’il n’en est pas toujours ainsi, et pour cela nous nous bornerons à donner un exemple.

Supposons que $p=2$, c’est-à-dire que la surface $W$ soit cinq fois connexe. Je supposerai de plus que les cycles $K'_1$ et $K'_2$ sont deux des cycles fondamentaux de $W$, à savoir :

$$K'_1=C_1,~~K'_2=C_3.$$

Je représenterai la surface $W$ par un polygone fuchsien $R_0$ de la troisième famille limité par quatre circonférences ne se coupant pas. Pour cela, nous n’avons qu’à tracer sur la surface $W$ les deux cycles $C_1$ et $C_3$ qui ne se coupent pas, à découper la surface le long de ces deux cycles regardés comme des coupures et à la développer ensuite sur un plan.

Les cycles $K''_1$ et $K''_2$ seront représentés alors sur ce plan par un certain nombre d’arcs de courbe allant d’un point du périmètre du polygone fuchsien $R_0$ à un autre point de ce périmètre.

Voici à quelles conditions sont assujettis ces arcs de courbe :

1° Ils ne doivent pas se couper mutuellement ; c’est là la condition nécessaire et suffisante pour que les cycles $K''_1$ et $K''_2$ ne soient pas bouclés et ne se coupent pas.

2° Considérons alors la série d’arcs dont l’ensemble représente le cycle $K''_1$. Ces arcs doivent être parcourus dans un certain ordre et chacun d’eux va d’un certain point initial situé sur le périmètre de $R_0$ à un certain point final situé également sur le périmètre de $R_0$. Observons que le périmètre de $R_0$ se compose de quatre cercles conjugués deux à deux ; à chaque point de l’un des cercles correspond sur le cercle conjugué un point que j’appelle le conjugué du premier.

Cela posé, le point final de chacun des arcs qui représentent $K''_1$ doit être conjugué du point initial de l’arc suivant, et le point final du dernier arc doit être le conjugué du pont initial du premier arc.

De même pour les arcs qui représentent $K''_2$.

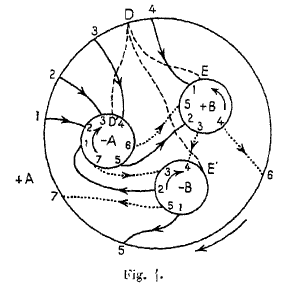
Voici l’explication de la figure : le périmètre de $R_0$ est représenté par les quatre cercles $+A, -A, +B, -B$ représentés en trait plein ; les cercles $+A$ et $-A$ sont conjugués et correspondent à $K'_1=C_1$ ; les cercles $+B$ et $-B$ sont conjugués et correspondent à $K'_2=C_3$ ; les cycles $K''_1$ et $K''_2$ sont représentés par des arcs de courbe allant d’un point à l’autre du périmètre de $R_0$.

Les arcs qui représentent $K''_1$ sont en trait plein ; ceux qui représentent $K''_2$ sont en trait pointillé. Une pointe de flèche placée sur le trait lui-même indique dans quel sens ce trait doit être parcouru.

Les points où ces arcs coupent les cercles $\pm A$ et $\pm B$ sont désignés par des numéros ; ces numéros nous font connaître en même temps quels sont ceux de ces points qui sont conjugués ; ainsi le point $+ B~5$ est conjugué de $-B~5$, le point $+ A~5$ de $- A~5$.

Près de chacun des quatre cercles $\pm A, \pm B$ est placée une flèche dont voici la signification ; quand un point décrit l’un des cercles dans le sens de la flèche, le point conjugué doit décrire le cercle conjugué dans le sens de la flèche.

On vérifie aisément qu’en suivant soit $+A$, soit $-A$, dans le sens de la flèche on rencontre successivement

$$1,2,3,4,5,6,7$$

et qu’en suivant soit $+B$, soit $-B$ dans le sens de la flèche on rencontre successivement

$$1,5,2,3,4.$$

L’ordre de conjugaison de nos points a donc été convenablement choisi.

Le cycle $K''_1$ est alors représenté par sept arcs qui se succèdent dans l’ordre suivant :

$$ \begin{array}{c} +A\,1 \text{ à } -A\,2\,;\, +A\,2 \text{ à } -A\,3\,;\\ +A\,3 \text{ à } -A\,4\,; \,+A\,4 \text{ à } +B\,1\,;\, -B\,1 \text{ à } +A\,5\,;\\ -A\,5 \text{ à } +B\,2\,;\, -B\,2 \text{ à } -A\,1. \end{array} $$

Le cycle $K''_2$ est représenté par les cinq arcs :

$$ \begin{array}{c} +B\,3 \text{ à } -B\,4\,;\,+B\,4\text{ à } +A\,6\,;\, -A\,6\text{ à } +B\,5\,;\\ -B\,5\text{ à } +A\,7\,; \,-A\,7\text{ à } -B\,3. \end{array} $$

Il est aisé de voir sur la figure que ces 12 arcs ne se coupent pas ; nos deux cycles ne sont donc pas bouclés et ne se coupent pas.

Nous pouvons donc construire une variété $V'$, admettant les cycles $K'_1=C_1$ et $K'_2=C_3$ pour cycles principaux et une variété $V''$ admettant les cycles $K''_1$ et $K''_2$ comme cycles principaux. La réunion des deux variétés $V'$ et $V''$ nous donnera $V$.

On s’en rendra mieux compte encore de la façon suivante.

Reprenons notre figure et découpons le polygone $R_0$ suivant les 12 arcs qui représentent $K''_1$ et $K''_2$ ; nous aurons ainsi décomposé $R_0$ en 10 polygones partiels ; recollons ensuite ces polygones les uns aux autres en collant chacun des arcs des diverses cercles $\pm A$, $\pm B$ aux arcs correspondants du cercle conjugué ; par exemple l’arc $+ A~3$, $+A~4$ à l’arc $- A~3$, $-A~4$ ; nous obtiendrons ainsi un nouveau polygone qui au même titre que $R_0$ représentera la surface $W$ avec cette différence que les coupures au lieu d’être faites suivant les cycles $K'_1$ et $K'_2$ seront faites suivant les cycles $K''_1$ et $K''_2$.

La figure ainsi obtenue est tout à fait pareille à la figure 1, mais la signification en est différente. Les cercles $+A$ et $-A$ représentent $K''_1$ et non plus $K'_1$, les cercles $+B$ et $-B$ représentent $K''_2$ ; les arcs en trait pointillé représentent $K'_2$.

Les points

$$\pm A\,1,\ \pm A\,2,\ \pm A\,3,\ \pm A\,4,\ \pm A\,6,\ \pm A\,5,\ \pm A\,7$$

représentent respectivement les points

$$\pm A\,1,\ \pm A\,2,\ \pm A\,3,\ \pm A\,4,\ \pm B\,1,\ \pm A\,5,\ \pm B\,2.$$

Les points

$$\pm B\,1,\ \pm B\,5,\ \pm B\,2,\ \pm B\,3,\ \pm B\,4$$

représentent respectivement

$$\pm A\,6,\ \pm B\,5,\ \pm A\,7,\ \pm B\,3,\ \pm B\,4.$$

On ne doit pas s’étonner de ce signe $\pm$ ; les deux points $+A\,1$ et $-A\,1$ correspondent, en effet, à un même point de la surface $W$.

L’identité des deux figures nous montre que la surface $W$ est homéomorphe à elle-même de telle façon qu’aux cycles

$$K'_1,\ K'_2,\ K''_1,\ K''_2$$

correspondent les cycles

$$K''_1,\ K''_2,\ K'_1,\ K'_2.$$

Cherchons à exprimer $K''_1$ et $K''_2$ en fonction de quatre cycles fondamentaux $C_1$, $C_2$, $C_3$, $C_4$. Pour cela nous n’avons qu’à appliquer la règle de la fin du paragraphe 4, et pour faciliter l’application de cette règle nos avons tracé en tirets $---$ les trois coupures $DD'$, $DE$, $DE'$ qui figurent dans son énoncé.

L’arc $+A\,1-A\,2$ part de $+A$, ce qui donne $+C_2$.

L’arc $+A\,2-A\,3$ part de $+A$, ce qui donne $+C_2$.

L’arc $+A\,3-A\,4$ part de $+A$, ce qui donne $+C_2$
et rencontre $DD'$ de gauche à droite, ce qui donne $+C_1$.

L’arc $+A\,4 +B\,1$ part de $+A$, ce qui donne $+C_2$
et rencontre $DE$ de droite à gauche, ce qui donne $-C_3$.

L’arc $-B\,1+A\,5$ part de $-B$, ce qui donne $+C_2$.

L’arc $-A\,5 + B\,2$ part de $-A$, ce qui donne $-C_2$
et rencontre $DE'$ de gauche à droite, ce qui donne $-C_4-C_3+C_4$.

L’arc $-B\,2-A\,1$ part de $-B$, ce qui donne $+C_4$.

Donc

$$K''_1 \equiv 3C_2 +C_1+C_2-C_3+C_4-C_2-C_4-C_3+2C_4.$$

Passons à $K''_2$.

L’arc $+B\,3 -B\,4$ part de $+B$, ce qui donne $-C_4$
et rencontre $DE'$ de droite à gauche, ce qui donne $-C_4+C_3+C_4$.

L’arc $+B\,4+A\,6$ part de $+B$, ce qui donne $-C_4$.

L’arc $-A\,6 +B\,5$ part de $-A$, ce qui donne $-C_2$
et rencontre $DE'$ de gauche à droite, ce qui donne $-C_4-C_3+C_4$.

L’arc $-B\,5 +A\,7$ part de $-B$, ce qui donne $+C_4$.

L’arc $-A\,7 -B\,3$ part de $-A$, ce qui donne $-C_2$.

Donc

$$K''_2 \equiv -2C_4+C_3-C_2-C_4-C_3+2C_4-C_2.$$

Nous avons donc

$$ \begin{array}{lll} K'_1 \equiv C_1,\ K'_2 \equiv C_3,\\ K''_1 \equiv 3C_2+C_1+C_2-C_3+C_4-C_2-C_4-C_3+2C_4,\\ K''_2 \equiv -2C_4+C_3-C_2-C_4-C_3+2C_4-C_2. \end{array}$$

Par rapport à $V$ nous avons les équivalences

$$ \tag{1} \left \{\begin{array}{ll} C_1+C_2-C_1-C_2+C_3+C_4-C_3-C_4 \equiv 0, \\ K'_1\equiv K'_2 \equiv 0,~~K''_1 \equiv 0,~~K''_2 \equiv 0. \end{array} \right. $$

Les équivalences $K'_1 \equiv K'_2 \equiv 0$ ou $C_1 \equiv C_3 \equiv 0$ permettent de simplifier les autres ; l’équivalence (1) se réduit à

$$C_2-C_2 +C_4-C_4 \equiv 0,$$

c’est-à-dire à une identité ; l’équivalence $K''_1 \equiv 0$ se réduit à

$$ \tag{2} 4C_2+C_4-C_2+C_4 \equiv 0 $$

et l’équivalence $K''_2 \equiv 0$ se réduit à

$$ \tag{3} -2C_4-C_2 + C_4-C_2 \equiv 0. $$

En résumé, il nous reste deux cycles distincts $C_2$ et $C_4$ entre lesquels nous n’avons pas d’autres équivalences que (2) et (3).

Si nous transformons ces équivalences en homologies, il vient

$$3C_2+2C_4 \sim 0,~~~-C_4-2C_2 \sim 0.$$

Le déterminant est égal à $-1$ ; nous sommes donc dans le cas où $\Delta = \pm 1$, où le nombre de Betti et les coefficients de torsion sont égaux à $1$. Et cependant $V$ n’est pas simplement connexe ; car son groupe fondamental ne se réduit pas à la substitution identique ; en d’autres termes, des équivalences (2) et (3) on ne peut déduire

$$C_2 \equiv 0,~~C_4 \equiv 0.$$

Pour le montrer, j’adjoins à (2) et à (3) l’équivalence

$$ \tag{4} -C_2 + C_4-C_2 +C_4 \equiv 0, $$

d’où

$$C_4-C_2+C_4-C_2 \equiv 0.$$

De (2), (3) et (4) on déduira

$$ \tag{5} \left \{\begin{array}{ll} -C_2+C_4-C_2+ C_4 \equiv 0, \\ 5C_2 \equiv 0,~~3C_4 \equiv 0. \end{array} \right. $$

Or, les relations (5) sont les relations de structure qui ont lieu entre les deux substitutions $C_2$ et $C_4$ qui engendrent le groupe icosaédrique. On ne saurait donc en déduire $C_2 \equiv 0$, $C_4 \equiv 0$, ni a fortiori déduire ces deux équivalences de (2) et (3) seulement.

Il y a donc deux cycles de $V$ qui ne sont pas équivalents à zéro ; donc $V$ n’est pas simplement connexe.

En d’autres termes, le groupe fondamental de $V$ ne saurait se réduire à la substitution identique, puisqu’il contient comme sous-groupe [1] le groupe icosaédrique.

Il resterait une question à traiter :

Est-il possible que le groupe fondamental de $V$ se réduise à la substitution identique, et que pourtant $V$ ne soit pas simplement connexe ?

En d’autres termes, peut-on tracer les cycles $K''_1$ et $K''_2$ de telle façon qu’ils ne soient pas bouclés et ne se coupent pas ; que les équivalences

$$K'_1 \equiv K'_2 \equiv 0,~~K''_1 \equiv K''_2 \equiv 0$$

entraînent les équivalences

$$C_1 \equiv C_2 \equiv C_3 \equiv C_4 \equiv 0$$

et que cependant la surface $W$ ne puisse être regardée comme homéomorphe à elle-même de telle façon qu’aux cycles $C_1, C_2, C_3, C_4$ correspondent les cycles $C'_1, C'_2, C'_3, C'_4$ ; que les équivalences

$$K'_1 \equiv K'_2 \equiv 0$$

entraînent $C'_1 \equiv C'_2 \equiv 0$ et réciproquement ; et qu’enfin les équivalences

$$K''_1 \equiv K''_2 \equiv 0$$

entraînent $C'_2 \equiv C'_4 \equiv 0$ et réciproquement ?

Mais cette question [2] nous entraînerait trop loin.