
|
> Homologie > Homologie singulière > Du groupe fondamental à l’homologie en degré 1 Du groupe fondamental à l’homologie en degré 1 |
Dans cet article on relie le groupe fondamental [1] et le groupe d’homologie singulière en degré $1$. On montre plus précisément que ce dernier est isomorphe à l’abélianisé du groupe fondamental. Ce résultat, implicitement énoncé par Poincaré dans le §12 de l’Analysis Situs [2], est un cas particulier d’un théorème d’Hurewicz.
Homotopie et homologie
Soit $X$ un espace topologique. Un $1$-simplexe singulier n’est rien d’autre qu’un chemin $f: [0,1]\to X$. Si $f$ est de plus un lacet, c’est-à-dire $f(0)=f(1)$, alors $\partial (f)=0$ et $f$ définit donc un cycle. On notera $\langle f\rangle \in H_1(X)$ la classe d’homologie associée au lacet $f$.
Si $f, g: [0,1] \to X$ sont des chemins homotopes, alors les $1$-chaînes associées sont homotopes dans $C_*(X)$, c’est-à-dire il existe $(K_i: C_i(X) \to C_{i+1}(X))_{i=0,1}$ tel que
$$f-g = \partial K_1 + K_0\partial .$$
En particulier, l’application $f\mapsto \langle f\rangle$ passe au quotient pour définir, pour tout point base $x_0\in X$, l’application $\pi_1(X,x_0) \to H_1(X)$ donnée par $[f]\mapsto \langle f\rangle$.
Démonstration. Le cycle $f$ induit un morphisme de complexes de chaînes
$$f_*: C_*(\Delta_1 ) \to C_*(X).$$
On a alors $f = f_*({\rm id}_{\Delta_1})$ et la première affirmation n’est alors rien d’autre que le lemme d’homotopie des chaînes. La seconde découle de la première puisque des cycles homotopes définissent la même classe en homologie.
C.Q.F.D
$$ $$
L’application $[f]\mapsto \langle f\rangle$ ne peut pas être un isomorphisme de groupes en général car :
- le groupe fondamental n’est pas toujours abélien contrairement à $H_1(X)$ ;
- le premier groupe d’homologie ne dépend pas du choix d’un point base contrairement au groupe fondamental.
Ces deux obstructions disparaissent si on se restreint aux espaces connexes par arcs dont le groupe fondamental est abélien. En fait, dans le cas général, il suffit de considérer l’abélianisé du groupe fondamental.
Énoncé du théorème
Étant donné un groupe $G$, on note $G^{ab}$ son abélianisé, c’est à dire son quotient $G/ [G,G]$ par le sous-groupe engendré par les commutateurs. C’est le plus grand quotient abélien de $G$. En particulier, si $H$ est un groupe abélien, tout morphisme de groupe $f :G\to H$ se factorise de manière unique au travers de $G^{ab}$ en $g : G^{ab}\to H$ :
$$\xymatrix{ G\ar[r]^{f} \ar[d]_{p} & H \\ G^{ab} \ar[ru]_{g} } $$
Si $X$ est un espace connexe par arcs, l’abélianisé $\pi_1(X,x_0)^{ab}$ ne dépend pas du point base (puisque deux choix différents coïncident à conjugaison près).
L’application $[f] \mapsto \langle f\rangle$ est un morphisme de groupes $\pi_1(X,x_0) \to H_1(X)$ pour tout point base $x_0$. Elle induit donc un unique morphisme de groupes $\phi: \pi_1(X,x_0)^{ab}\to H_1(X)$.
Si de plus $X$ est connexe par arcs, $\phi: \pi_1(X,x_0)^{ab}\to H_1(X)$ est un isomorphisme.
Démonstration
Bien qu’assez intuitif, ce théorème n’est pas complètement évident et il faut faire un peu attention. Par exemple, un $1$-cycle, n’est pas toujours donné par (la $1$-chaîne associée à) un lacet. Ainsi si $f, g: [0,1]\to X$ sont deux chemins tels que $f(0)=g(1)$ et $f(1)=g(0)$, la $1$-chaîne $f+g$ est un $1$-cycle qui est différent du $1$-cycle donné par le lacet $f\cdot g$ obtenu par concaténation de $f$ et $g$ (on va néanmoins voir que ces deux chaînes sont homotopes). De manière générale, on peut montrer que tout un cycle est une combinaison linaire finie de lacets subdivisés.
Commençons par montrer que $[f]\mapsto\langle f\rangle$ est bien un morphisme de groupes.
Soient $f,g:[0,1]\to X$ des chemins continus tels que $f(1)=g(0)$. On note $f \cdot g: [0,1]\to X$ leur concaténation. Alors, la $1$-chaîne singulière $f+g- f\cdot g$ est un bord (c’est à dire de la forme $\partial z$).
En particulier, il suit que $[f] \mapsto \langle f\rangle$ est un morphisme de monoïdes.
Démonstration du lemme 1. On va construire explicitement $z$ tel que $f+g- f\cdot g=\partial (z)$. Cette construction est illustrée sur la figure ci-dessous. Soit $z: \Delta_2\to X$ le $2$-simplexe singulier qui est constant sur les perpendiculaires à l’arête entre les sommets $0$ et $2$, qui vaut $f$ sur l’arête entre les sommets $0$ et $1$ (arête identifiée au simplexe standard $\Delta_1$) et $g$ sur l’arête entre les sommets $1$ et $2$.
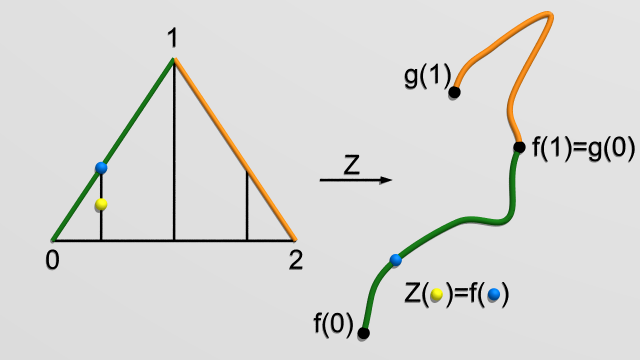
On a alors que la restriction de $h$ à l’arête entre les sommets $0$ et $2$ est $f \cdot g$ et il suit que $\partial (z) = g -f \cdot g +f$.
C.Q.F.D.
$$ $$
Soient $f : [0,1]\to X$ un chemin continu et $\overline{f}:[0,1]\to X$ le même chemin parcouru dans le sens opposé ($\overline{f}(t)=f(1-t)$ pour tout $t\in[0,1]$). Alors, la $1$-chaîne singulière $f+\overline{f}$ est un bord (c’est-à-dire de la forme $\partial y$).
Démonstration du lemme 2. Par le lemme 1, il suffit de montrer que $f \cdot \overline{f} $ est un bord. Or, $f\cdot \overline{f}$ est homotope au lacet constant $t\mapsto f(0)$. Par le lemme 0, $f \cdot \overline{f} $ est donc un bord.
C.Q.F.D.
$$ $$
L’application $[f] \mapsto \langle f\rangle$ de $\pi_1(X,x_0)$ dans $H_1(X)$ est un morphisme de groupes.
Le morphisme $[f] \mapsto \langle f\rangle$ se factorise donc de manière unique sous la forme
$$\pi_1(X,x_0) \to \pi_1(X,x_0)^{ab} \stackrel{\phi}\to H_1(X). $$
Ceci démontre la première partie du théorème de Hurewicz-Poincaré. Montrons maintenant que $\phi$ est un isomorphisme lorsque $X$ est connexe par arcs. Pour cela, construisons un inverse $\psi$. Profitant de la connexité par arcs de $X$, on fixe, pour tout $x\in X$, un chemin continu $\lambda_x:[0,1]\to X$ tel que $\lambda_x (0)=x_0$ et $\lambda_x (1)= x$. On choisit, pour se simplifier la vie, $\lambda_{x_0}(t)=x_0$ le chemin constant. Notons que $x\mapsto \lambda_{x}$ s’étend en un morphisme $C_0(X)\to C_1(X)$ par linéarité.
Les chemins ainsi construits nous permettent de transformer tout $1$-simplexe singulier $\sigma:[0,1]\to X$ en le lacet
$$\lambda_{\sigma(0)} \cdot \sigma \cdot \overline{\lambda_{\sigma(1)}}.$$
Par linéarité, ceci s’étend en une application linéaire $\psi: C_1(X) \to \pi_1(X,x_0)^{ab} $.
Si $c=\partial(z)$ est un bord, alors $\psi(c) =1 \in \pi_1(X,x_0)^{ab} $.
En particulier, par passage au quotient, $\psi$ induit bien une application linéaire encore notée $\psi$ de $H_1(X)$ dans $ \pi_1(X,x_0)^{ab}$.
Démonstration du lemme 3. Notons $z_{\langle s_i, s_j\rangle}: [0,1]\to X$ les restrictions de $z$ à la face de sommets (ordonnés) $s_i, s_j$. Par linéarité, on a
$$\begin{array}[rcl] ~\psi(\partial(c)) &=& \psi(z_{\langle s_1, s_2\rangle}) -\psi(z_{\langle s_0, s_2\rangle})+\psi(z_{\langle s_0, s_1\rangle})\\ &=& \psi(z_{\langle s_0, s_1\rangle})+\psi(z_{\langle s_1, s_2\rangle})+\psi(\overline{z_{\langle s_0, s_2\rangle}})\\ &=&\lambda_{s_0} \cdot z_{\langle s_0, s_1\rangle} \overline{\lambda_{s_1}} \cdot \lambda_{s_1} \cdot z_{\langle s_1, s_2\rangle} \overline{\lambda_{s_2}} \cdot \lambda_{s_2} \cdot \overline{z_{\langle s_0, s_2\rangle}} \cdot \lambda_{s_0}\\ &= & \lambda_{s_0}\cdot z_{\langle s_0, s_1\rangle} \cdot z_{\langle s_1, s_2\rangle} \cdot \overline{z_{\langle s_0, s_2\rangle}} \cdot \lambda_{s_0}\\ &=& 1 \end{array}$$
car le $2$-simplexe singulier $z$ définit une homotopie entre $z_{\langle s_0, s_1 \rangle} \cdot z_{\langle s_1, s_2 \rangle} \cdot \overline{z_{\langle s_0, s_2 \rangle}}$ et le lacet constant $s_0$.
C.Q.F.D.
$$ $$
Si $f$ est un lacet pointé en $x_0$, on a que
$$ \psi \circ \phi ([f]) =[\lambda_{x_0} \cdot f \cdot \overline{\lambda_{x_0}}] =[f]$$
dans l’abélianisé $\pi_1(X,x_0)^{ab}$. Pour conclure que $\psi$ est bien un inverse de $\phi$, ce qui terminera la preuve du théorème d’Hurewicz-Poincaré, il suffit maintenant de montrer le lemme suivant.
Soit $c\in C_1(X)$. On a
$$\phi \circ \psi(c) = [c -\lambda_{\partial(c)}] \in H_1(X).$$
Il suit en effet du lemme appliqué à un cycle que $\phi \circ \psi$ est l’identité en homologie.
Démonstration du lemme 4. Par linéarité, il suffit de démontrer le lemme sur un $1$-simplexe singulier $\sigma$. On a
$$\phi\circ \psi(\sigma) =\phi( [\lambda_{\sigma(0)}\cdot \sigma \cdot \overline{\lambda_{\sigma(1)}}]) = [\lambda_{\sigma(0)}+\sigma -\lambda_{\sigma(1)}]$$
où la dernière égalité résulte du lemme 1.
C.Q.F.D.
$$ $$

