
|
> Homologie > Homologie singulière > Homologie singulière : définition et premières propriétés Homologie singulière : définition et premières propriétés |
Dans cet article, on associe des groupes d’homologie à un espace topologique quelconque. L’idée générale de l’homologie est de mesurer la complexité d’un espace en considérant les « variétés de dimension $p$ » que l’on peut faire entrer dans $V$ sans que certaines d’entre elles ne forment le bord d’une « variété » de dimension $p+1$. Pour définir l’homologie singulière, on élargit la classe des « variétés », afin d’autoriser n’importe quelle image continue d’un simplexe. On n’y voit plus rien mais on peut dérouler facilement les définitions jusqu’à obtenir une théorie homologique générale et naturelle. Calculer les groupes d’homologie ainsi obtenus est une autre histoire qui débute ici.
Chaînes singulières
Soit $X$ un espace topologique. Pour tout $i\in\mathbb{N}$, un $i$-simplexe singulier de $X$ est une application continue
$$\sigma : \Delta_i \to X,$$
où
$$\Delta_i = \{(x_0 , \ldots , x_i) \in \mathbb{R}^{i+1} \; \big| \; x_k \geq 0 , \ \sum_{k=0}^ {i} x_k = 1 \}$$
est le simplexe standard de dimension $i$.
Les simplexes standards de dimension $0$, $1$ et $2$ sont représentés sur la figure suivante.
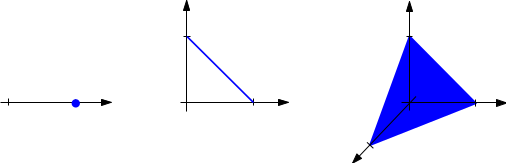
On note [1] $C_i (X) = C_{i,\mathrm{sing}} (X)$ le $\mathbb Z$-module libre engendré par l’ensemble de tous les $i$-simplexes singuliers de $X$. Chaque élément de $C_i (X)$ est donc une combinaison linéaire de la forme
$$\sum_{\sigma: \Delta_i \to X} c_{\sigma} \sigma$$
où seulement un nombre fini des entiers relatifs $c_\sigma$ est non nul. Les éléments de $C_i (X)$ sont appelés $i$-chaînes singulières.
Pour $i\ge 1$, on définit une application bord $\partial : C_i (X) \to C_{i-1} (X)$ de la manière suivante. Commençons par définir l’image d’un $i$-simplexe singulier $\sigma:\Delta_i\to X$. Pour tout $k=0 , \ldots , i$, on obtient un $(i-1)$-simplexe singulier $\partial_k \sigma$ en composant l’application linéaire
$$(x_0 , \ldots , x_{i-1})\mapsto (x_0 , \ldots , x_{k-1} ,0 , x_k , \ldots , x_{i-1}),$$
de $\Delta_{i-1} \subset \mathbb{R}^i$ vers la $k$-ème face $\{x_k =0 \}$ de $\Delta_i$, par l’application $\sigma$. On pose alors :
$$\partial \sigma = \sum_{k=0}^i (-1)^k \partial_k \sigma.$$
Maintenant qu’on a défini l’image d’un $i$-simplexe singulier quelconque, il ne reste plus qu’à étendre par linéarité en une application $\partial : C_i (X) \to C_{i-1} (X)$.
Pour $i=0$, on pose $C_{-1}(X)=\{0\}$ et on définit $\partial : C_0 (X) \to C_{-1} (X)$ comme l’application nulle.
Une $0$-chaîne singulière est donc juste une combinaison linéaire finie de points de $X$ alors qu’une $1$-chaîne est une combinaison linéaire de chemins (paramétrés) dans $X$. Le bord d’une telle $1$-chaîne est la combinaison linéaire correspondante des différences entre les extrémités des chemins.
Cycles, bords et homologies
On démontre comme pour l’homologie simpliciale que l’opérateur $\partial$ fait des chaînes singulières un complexe.
On a $\partial \circ \partial =0$.
Démonstration. Il suffit de démontrer que $\partial\circ\partial\sigma=0$ pour tout $i$-simplexe singulier $\sigma$. La démonstration repose sur l’observation suivante (qui découle immédiatement des définitions des opérateurs $\partial_k$, $\partial_j$ et $\partial_{k-1}$ ci-dessus) : si $k>j$, alors $\partial_j\partial_k\sigma=\partial_{k-1}\partial_j\sigma$. En utilisant cette observation, on obtient
$$\begin{array}[crcl] ~&\partial \circ \partial \sigma &=&\sum_{k=0}^i\sum_{j=0}^{i-1}(-1)^{k+j}\partial_j\partial_k\sigma\\ ~&~&=&\sum_{k=1}^i\sum_{j=0}^{k-1}(-1)^{k+j}\partial_j\partial_k\sigma+\sum_{j=0}^{i-1}\sum_{k=0}^{j}(-1)^{k+j}\partial_j\partial_k\sigma\\ ~&~&=&\sum_{k=1}^i\sum_{j=0}^{k-1}(-1)^{k+j}\partial_{k-1}\partial_j\sigma+\sum_{j=0}^{i-1}\sum_{k=0}^{j}(-1)^{k+j}\partial_j\partial_k\sigma\\ ~&~&=&\sum_{k=0}^{i-1}\sum_{j=0}^{k-1}(-1)^{k+j-1}\partial_{k}\partial_j\sigma+\sum_{j=0}^{i-1}\sum_{k=0}^{j}(-1)^{k+j}\partial_j\partial_k\sigma\\ ~&~&=&0. \end{array}$$
CQFD
$$ $$
On en déduit les notions de cycles, bords et homologie. Une $i$-chaîne $c \in C_i (X)$ est un $i$-cycle [2] si son bord est nul, c’est-à-dire si $\partial c = 0$. On note
$$Z_i (X) = \mathrm{ker} (\partial : C_i (X) \to C_{i-1} (X))$$
le sous-module des $i$-cycles. On a en particulier $Z_0(X)=\mathrm{ker}(\partial : C_0(X)\to 0)=C_0(X)$.
Une $i$-chaîne $c \in C_i (X)$ est un bord [3] si elle est le bord d’une $(i+1)$-chaîne. On note
$$B_i (X) = \mathrm{im} (\partial : C_{i+1} (X) \to C_{i} (X))$$
le sous-module des $i$-bords. Le lemme ci-dessus assure que tout $i$-bord est un $i$-cycle, c’est-à-dire que $B_i (X)$ est un sous-module de $Z_i(X)$.
Le groupe quotient
$$H_i (X) = Z_i (X) / B_i (X)$$
est appelé $i$-ème groupe d’homologie (singulière) de l’espace topologique $X$.
$$H_i (X) \cong \bigoplus_{\alpha} H_i (X_{\alpha}).$$
Soit $X=\{ *\}$ l’espace topologique réduit à un point. Montrons que
$$H_0 (X) = \mathbb{Z} \mbox{ et } H_i (X) = 0 \mbox{ si } i >0.$$
En effet $C_i = C_i(X) = \mathbb{Z}$ est engendré par l’unique $i$-simplexe singulier $\sigma_i : \Delta_i \to X$ (l’application constante). De plus, pour $i>0$, on a $\partial_k \sigma_i = \sigma_{i-1}$, donc
$$\partial \sigma_i = \sum_{k=0}^i (-1)^k \sigma_{i-1} = \left\{ \begin{array}{ll} \sigma_{i-1} & \mbox{ si } i \mbox{ est pair}, \\ 0 & \mbox{ sinon}. \end{array} \right.$$
Les groupes d’homologie de $X$ sont donc triviaux sauf en degré $0$.
Si $X$ est un espace topologique, le groupe $H_0 (X )$ est le groupe abélien libre engendré par les composantes connexes par arcs de $X$. De plus, pour tout point $x \in X$, la classe d’homologie $[x]$ est un générateur du facteur libre, isomorphe à $\mathbb{Z}$, qui correspond à la composante connexe par arcs de $X$ qui contient $x$.
Démonstration.
D’après la propriété précédente, on peut supposer que $X$ est connexe par arcs (et non vide). Le module $C_0 (X)$ est libre engendré par les points de $X$. Considérons le morphisme $\phi : C_0 (X) \to \mathbb{Z}$ qui vaut $1$ sur chaque point de $X$. Il est surjectif. Montrons que son noyau est $B_0(X)$. Si $c$ est un $1$-simplexe, alors $\phi(\partial c)=0$ et $B_0(X)\subset\mathrm{ker}(\phi)$. Réciproquement, soit $c$ une $0$-chaîne telle que $\phi(c)=0$. Alors, on peut écrire
$$c = -\sigma_0+\sigma_1+...-\sigma_{2n}+\sigma_{2n+1}$$
où chaque $0$-simplexe $\sigma_k$ correspond à un point de $X$. Comme $X$ est connexe par arcs, pour tout $i\in\{0,..,n\}$, il existe un lacet $\lambda_i$ reliant les points associés à $\sigma_{2i}$ et $\sigma_{2i+1}$. On a alors $\partial \lambda_i=\sigma_{2i+1}-\sigma_{2i}$ et $c$ est un bord. Ainsi $\mathrm{ker}(\phi)=B_0(X)$. Comme $Z_0(X) = C_0 (X)$ le morphisme $\phi$ induit un isomorphisme de $H_0 (X)$ sur $\mathbb{Z}$.
C.Q.F.D.
$$ $$
À ce stade, l’espace réduit à un point est essentiellement le seul espace dont il soit facile de calculer l’homologie singulière ! Par ailleurs contrairement aux complexes polyédraux/simpliciaux, le complexe des chaînes singulières d’une variété (même du point !) est non-trivial et même de dimension infinie (sauf pour une réunion finie de points) en tout degré.
Naturalité de l’homologie singulière

- L’effet fonctoriel sur Homer Simpson
Qu’a-t-on gagné à introduire cette théorie homologique plus abstraite que l’homologie polyédrale ou même l’homologie à la Poincaré ? La réponse est qu’elle est naturelle — on dit aussi fonctorielle — par rapports aux applications continues :
Si $X$ et $Y$ sont deux espaces topologiques et $f:X \to Y$ est une application continue, alors $f$ induit un morphisme de complexes de chaînes $f_* : C_{\bullet} (X) \to C_{\bullet} (Y)$ [4] qui à un simplexe singulier $\sigma$ associe le simplexe singulier $f\circ \sigma: \Delta_i\to Y$.
Comme $f_*$ est un morphisme de complexes, il passe au quotient pour définir une application — toujours notée $f_*: H_*(X)\to H_*(Y)$ — entre les groupes d’homologie singulière.
Soient $f$ et $g$ deux applications homotopes de $X$ dans $Y$. Alors les applications induites $f_*$ et $g_*$ de $H_{\bullet} (X)$ dans $H_{\bullet} (Y)$ coïncident.
Le résultat découle alors du lemme (plus fort) suivant.
Soient $f$ et $g$ deux applications homotopes de $X$ dans $Y$. Alors il existe une homotopie de chaînes entre $f_*$ et $g_*$, c’est-à-dire une famille de morphismes $K= (K_i : C_i(X) \to C_{i+1} (Y) )$ vérifiant
$$\tag{1} K_{i} \partial + \partial K_{i+1} = g_* - f_*,$$
pour tout $i$.
Démonstration de la proposition.
Du lemme, il découle que $g_*$ et $f_*$ coïncident en homologie puisque si $z$ est un $i$-cycle, $g_*(z)-f_*(z) =\partial K_i(z)$ est un bord, ce qui termine la preuve de la proposition.
C.Q.F.D.
$$ $$
Démontrons maintenant le lemme.
Soient $\iota : X \to X \times [0,1]$ et $\iota ' : X \to X \times [0,1]$ les applications définies par $\iota (x) = (x,0)$ et $\iota ' (x) = (x, 1)$. Si $h$ est une homotopie entre $f$ et $g$, alors $f = h \circ \iota$ et $g = h \circ \iota '$. Il suffit donc de montrer que $\iota_*$ et $\iota_* '$ sont homotopes. Par linéarité il suffit de construire les $K_i$ sur les $i$-simplexes singuliers.
Considérons donc un $i$-simplexe singulier $\sigma : \Delta_i \to X$. Il lui correspond une application $\sigma \times \mathrm{id} : \Delta_i \times [0,1] \to X \times [0,1]$. L’idée est alors de décomposer le prisme $\Delta_i \times [0,1]$ en $(i+1)$ simplexes de dimension $i+1$.
Notons $(x_0, \ldots , x_i ; \lambda)$ les coordonnées de $\Delta_i \times [0,1] \subset \mathbb{R}^{i+1} \times [0,1]$. Alors pour tout $k\in \{ 0 , \ldots , i\}$, le $k$-ème simplexe de la décomposition du prisme [5] est constitué des points $(x_0 , \ldots , x_i , \lambda )$ tels que
$$x_0 + \ldots + x_{k-1} \leq \lambda \leq x_0 + \ldots + x_{k}.$$
Ce simplexe coïncide avec le simplexe obtenu comme enveloppe convexe des points $(s_0\times \{1\}, \dots, s_{k}\times \{1\}, s_{k}\times \{0\}, s_{k}\times \{0\}, s_{i}\times \{1\})$ où on a noté $s_0,\dots, s_i$ les sommets du simplexe standard.
Chacun de ces simplexes est en outre muni de l’orientation induite par l’orientation naturelle du prisme ; ces orientations sont compatibles. En « restreignant » l’application $\sigma \times \mathrm{id}$ à chacun de ces simplexes et en formant la somme, on obtient une chaîne singulière de dimension $i+1$ dans $X \times [0,1]$.
Plus précisément, si $t_0,\dots,t_k$ sont des sommets du prisme, on note $[t_0,\dots,t_k]$ le simplexe induit [6]. On pose alors
$$K_i(\sigma) =\sum_{k=0}^i (-1)^k (\sigma \times \mathrm{id})_{ \vert [s_0\times \{1\}, \dots, s_{k}\times \{1\}, s_{k}\times \{0\},\dots, s_{i}\times \{0\}]}.$$
Commençons par vérifier (1) quand $\sigma$ est un $1$-simplexe singulier. On a alors,
$$K(\sigma)=(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_0\times\{0\},s_1\times\{0\}]}-(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_1\times\{1\},s_1\times\{0\}]}$$
$$\begin{array}[ccl] ~\partial K_1(\sigma)&=& {\color{blue}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{0\},s_1\times\{0\}]}}} -{\color{orange}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_1\times\{0\}]}}} +{\color{red}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_0\times\{0\}]}}}\\ ~&~& -{\color{red}{(\sigma\times \mathrm{Id})_{\vert[s_1\times\{1\},s_1\times\{0\}]}}} +{\color{orange}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_1\times\{0\}]}}} -{\color{blue}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_1\times\{1\}]}}}\\ ~&=& {\color{blue}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{0\},s_1\times\{0\}]}}} -{\color{blue}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_1\times\{1\}]}}} +{\color{red}{(\sigma\times \mathrm{Id})_{\vert[s_0\times\{1\},s_0\times\{0\}]}}}\\ ~&~& -{\color{red}{(\sigma\times \mathrm{Id})_{\vert[s_1\times\{1\},s_1\times\{0\}]}}}\\ ~&=&-{\color{red}{K_0(\partial\sigma)}}+{\color{blue}{\iota\circ\sigma}}-{\color{blue}{\iota'\circ\sigma}}. \end{array}$$
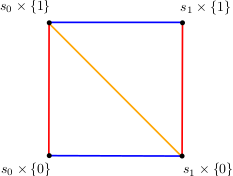
Dans le cas général, le bord de $K_i(\sigma)$ est constitué des simplexes singuliers $\iota \circ \sigma$ et $\iota ' \circ \sigma$ — correspondant aux bases du prisme --- ainsi que d’une chaîne singulière — correspondant à la surface latérale du prisme et donc au prisme sur le bord de $\sigma$. Les contributions des faces intérieures du prisme se compensent. L’identité (1) sur le simplexe singulier $\sigma$ s’en déduit.
C.Q.F.D
$$ $$
[1] On mettra l’indice sing quand il sera nécessaire de distinguer les complexes de chaînes singulières des simpliciales ; et de même avec les groupes
d’homologie.
[2] on dit aussi qu’elle est fermée
[3] on dit aussi qu’elle est exacte
[4] c’est à dire une famille d’applications linéaires qui commutent avec le bord : $\partial f = f \partial$.
[5] Il est vrai que cette décomposition est bien une décomposition en complexes simpliciaux du prisme. Cependant, on n’a pas besoin de vérifier strictement ce point ; il suffit de vérifier que la formule donnée pour $K_i$ marche
[6] Ce simplexe est identifié au simplexe standard par l’unique application affine envoyant les sommets du $k$-simplexe standard sur $t_0,\dots,t_k$ (en respectant l’ordre).


