Théorème des petites chaînes

Dans cet article on démontre le théorème des petites chaînes selon lequel dans le calcul des groupes d’homologie singulière on peut ne considérer que des combinaisons de simplexes singuliers à support dans des ouverts arbitrairement petits de l’espace topologique considéré. C’est le point clé du théorème d’écrasement que nous démontrons ici.

Le théorème des petites chaînes

Soient $X$ un espace topologique et $(U_{\alpha})$ un recouvrement ouvert de $X$. Pour tout $i\in \mathbb{N}$, on considère le sous-complexe $C_{i}\left (X^{\{ U_{\alpha} \}}\right)$ de $C_{i} (X)$ engendré par les simplexes singuliers d’image contenue dans l’un des $U_{\alpha}$.

L’idée est de construire l’application inverse en transformant une $i$-chaîne en une petite chaîne par subdivisions barycentriques des $i$-simplexes standards. Avant d’expliquer la subdivision barycentrique (voir aussi cet article), commençons par quelques notations.

Soient $s_0, \ldots , s_i$ les sommets du $i$-simplexe standard $\Delta_i$. Étant donné $i+1$ points $x_0 , \ldots , x_i$ d’un espace euclidien $\mathbb{R}^n$, notons $[x_0 , \ldots , x_i]$ l’unique application affine de $\Delta_i$ dans $\mathbb{R}^n$ qui envoie $s_k$ sur $x_k$ pour $0 \leq k \leq i$. Si $S$ est un sous-ensemble de $\{0 , 1 , \ldots , i \}$ notons enfin $b_S$ le barycentre des points $\{ s_k \; \big| \; k \in S\}$.

Soit $\alpha$ un élément du groupe symétrique $S_{i+1}$ des transformations de $\{0 , 1 , \ldots , i \}$. On lui associe le $i$-simplexe singulier $\beta_{\alpha} : \Delta_i \to \Delta_i$

$$\beta_{\alpha} = [ b_{\{\alpha(0)\}} , b_{\{\alpha (0) , \alpha (1)\}}, \ldots , b_{\{\alpha (0) , \alpha (1) , \ldots , \alpha (i)\}}].$$

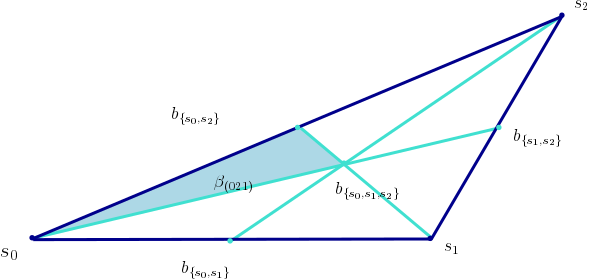
Posons alors, pour tout $i$-simplexe singulier $\sigma$,

$$\mathrm{Sd} (\sigma ) = \sum_{\alpha \in S_{i+1}} \mathrm{sgn} (\alpha) \ \sigma \circ \beta_{\alpha}.$$

En prolongeant par linéarité, on vérifie que l’on obtient un morphisme de complexes $\mathrm{Sd} : C_{\bullet} (X) \to C_{\bullet} (X)$.

Voici un exemple de subdivision barycentrique d’une chaîne.

Démonstration. Il s’agit de construire des morphisme $K_i : C_i (X) \to C_{i+1} (X)$ tels que

$$\tag{1} \partial \circ K_i + K_{i-1} \circ \partial = \mathrm{id} - \mathrm{Sd}.$$

On procède par récurrence sur $i \in \mathbb{N}$.

Comme $\mathrm{Sd}$ est égale à l’identité en degré $0$, on peut prendre $K_0 =0 (=K_{-1})$.

Supposons donc construits $K_0 , \ldots , K_{i-1}$. Par abus de langage on voit $\Delta_i$ comme le $i$-simplexe singulier $\mathrm{id}_{\Delta_i}$ de $\Delta_i$. Par hypothèse de récurrence appliquée à $(i-1)$-chaîne singulière $\partial \Delta_i$ dans $X=\Delta_i$, on a

$$\partial \Delta_i - \mathrm{Sd} (\partial \Delta_i ) = \partial \circ K_{i-1} (\partial \Delta_i)$$

et donc

$$\partial (\Delta_i - \mathrm{Sd} (\Delta_i) - K_{i-1} (\partial \Delta_i )) = 0.$$

Comme $\Delta_i$ est contractile, il existe alors une $(i+1)$-chaîne singulière $\sigma_{i+1} \in C_{i+1} (\Delta_i)$ telle que

$$\tag{2} \Delta_i - \mathrm{Sd} (\Delta_i) - K_{i-1} (\partial \Delta_i ) = \partial \sigma_{i+1}.$$

Soit maintenant un $i$-simplexe singulier de $X$. Posons $K_i (\sigma ) = \sigma \circ \sigma_{i+1} \in C_{i+1} (X)$. En prolongeant par linéarité on obtient un morphisme de modules $K_i : C_i (X) \to C_{i+1} (X)$ qui, d’après (2), vérifie la relation (1).

C.Q.F.D.

$$ $$

Démonstration. Par linéarité on peut supposer que $\sigma$ est un $i$-simplexe singulier. Les ouverts $V_{\alpha} = \sigma^{-1} (U_{\alpha})$ forment un recouvrement de l’espace compact $\Delta_i$. Il existe donc $\varepsilon >0$ tel que si $A \subset \Delta_i$ vérifie $\mathrm{diam} (A) \leq \varepsilon$, alors il existe un $\alpha$ tel que $A \subset V_{\alpha}$. Le lemme découle alors de l’inégalité

$$\mathrm{diam} \left(\mathrm{Sd}^r (\Delta_i )\right) \leq \left( \frac{i}{i+1} \right)^r \mathrm{diam} (\Delta_i ).$$

Il suffit de vérifier cette inégalité sur les sommets d’un élément de la subdivision barycentrique d’un simplexe $[x_0,\dots,x_i]$ (exercice).
C.Q.F.D.

$$ $$

Démonstration du théorème. On peut maintenant terminer la démonstration du théorème. Si $z$ est un cycle singulier de $X$, pour tout $r \in \mathbb{N}$, $\mathrm{Sd}^r (z)$ est aussi un cycle singulier et, en itérant le premier lemme, on montre que $\mathrm{Sd}^r (z)$ est homologue à $z$. Il découle donc du second lemme que l’application $H_{\bullet} (X^{\{ U_{\alpha} \}}) \to H_{\bullet} (X)$ est surjective. Elle est aussi injective : si $z = \partial t$ alors $\mathrm{Sd}^r (z) = \mathrm{Sd}^r (\partial t) = \partial \mathrm{Sd}^r (t)$.

C.Q.F.D.

$$ $$

Quelques remarques

Le théorème des petites chaînes s’étend sans difficulté au cas relatif. En effet, pour $A\subset X$, on dispose aussi du complexe $C_\bullet(A^{\{ A\cap U_{\alpha} \}})$ de petites chaînes relatives au recouvrement $\{ A\cap U_{\alpha} \}$ de $A$. On a un diagramme commutatif de suite exacte courte de complexes :

$$\xymatrix{C_\bullet(A^{\{A\cap U_{\alpha} \}}) \ar@{^{(}->}[r] \ar[d] & C_\bullet(X^{\{ U_{\alpha} \}}) \ar@{->>}[r]\ar[d] & C_\bullet(X^{\{ U_{\alpha} \}}, A^{\{ A\cap U_{\alpha} \}}) \ar[d] \\ C_\bullet(A)\ar@{^{(}->}[r] & C_\bullet(X) \ar@{->>}[r] & C_\bullet(X,A)} $$

où les flèches verticales sont les inclusions naturelles. Les deux flèches verticales les plus à gauche sont des quasi-isomorphismes par le théorèmes des petites chaînes ; donc la troisième flèche $C_\bullet(X^{\{ U_{\alpha} \}}, A^{\{ A\cap U_{\alpha} \}})\to C_\bullet(X,A)$ aussi par la proposition énoncée ici.

Le théorème des petites chaînes reste vrai si on suppose que les $U_\alpha$ sont des sous-espaces quelconques dont les intérieurs $\overset{\circ}{U_\alpha}$ forment un recouvrement ouvert de $X$.