Évolution de la topologie des sous-niveaux

Comme annoncé dans l’introduction, la théorie de Morse s’intéresse en premier lieu à l’évolution de la topologie des sous-niveaux d’une fonction lisse $f$ [1] sur une variété $M$ lorsque l’on balaye l’ensemble des valeurs prises par $f$. Pour tout réel $a$, on notera $M^a$ le sous-$a$-niveau de la fonction $f$, c’est-à-dire

$$M^a=f^{-1}(]-\infty;a])=\{x \in M;\ f(x)\leq a\}.$$

On se limitera ici au cas où tous les sous-niveaux sont compacts, ce qui est notamment le cas si $M$ est elle-même compacte [2].

Dans un premier temps, on montre que tant qu’on ne rencontre pas de valeur critique, la topologie des sous-niveaux ne change pas. On verra ensuite que le franchissement d’un niveau critique non-dégénéré résulte en l’attachement d’un certain nombre d’anses, l’outil principal pour cela étant le Lemme de Morse, auquel nous consacrons un article distinct. On déduira ici de ces deux résultats que toute variété compacte possède une décomposition en anses.

Intervalle sans valeur critique

L’idée de la démonstration est relativement simple : il s’agit de « rétracter » $M^b$ sur $M^a$ en poussant le long de trajectoires orthogonales aux lignes de niveau de $f$ (l’animation suivante montre au contraire « l’étirement » de $M^a$ sur $M^b$).

On peut faire cela via une famille à un paramètre de difféomorphismes, ce qui donne en particulier l’énoncé ci-dessus, ou via une famille à un paramètre d’applications qui sont l’identité sur $M^a$ (mais ne peuvent alors pas toutes être injectives), auquel cas on obtient une rétraction par déformation de $M^b$ sur $M^a$, et en particulier une équivalence d’homotopie entre les deux.

Précisons un peu l’idée intuitive ci-dessus. On commence par munir $M$ d’une métrique riemannienne. Le gradient de $f$ est alors un champ de vecteurs non nul sur $f^{-1}([a,b])$. En normalisant le gradient de $f$, on construit facilement un champ de vecteurs $X$ sur $M$, nul sur le complémentaire d’un voisinage compact de $f^{-1}([a,b])$, et tel que la dérivée de $f$ le long de $X$ soit constante égale à 1 sur $f^{-1}([a,b])$, de sorte que $f$ croît comme le temps le long des portions d’orbites comprises dans $f^{-1}([a,b])$. Un tel champ de vecteurs à support compact a pour flot un groupe à un paramètre $\phi_t$ de difféomorphismes de $M$ [3] et on vérifie immédiatement que $\phi_{b-a}$ est un difféomorphisme de $M^a$ sur $M^b$. De plus, la famille à un paramètre $r_t:M^b \longrightarrow M^b$ telle que la restriction de $r_t$ au sous-niveau $M^a$ soit l’identité et égale à $\phi_{t(a-f(x))}$ si $f(x)$ est compris entre $a$ et $b$, est une rétraction de $M^b$ sur $M^a$.

C.Q.F.D.

$$ $$

Avant de passer au théorème général dans le cas du franchissement d’une valeur critique, notons que ce résultat, combiné au lemme de Morse dans le cas de points critiques d’indices extrémaux, permet de démontrer le joli corollaire suivant :

Démonstration du théorème de Reeb

En effet, les deux points critiques ne peuvent être que le minimum $m$ et le maximum $m'$ de la fonction.
D’après le Lemme de Morse, pour $\epsilon$ suffisamment petit, $f^{-1}([m,m+\epsilon])$ et $f^{-1}([m'-\epsilon,m'])$ sont des cellules de dimension $n$ et le théorème précédent assure que $f^{-1}([m,m+\epsilon])$ et $f^{-1}([m,m'-\epsilon])$ sont difféomorphes puisque $f$ n’a pas de valeur critique entre $m+\epsilon$ et $m'-\epsilon$.
On construit alors facilement un homéomorphisme entre $M$ et $\mathbf{S}^n$ en recollant le long des bords.
Notons que rien n’assure que l’homéomorphisme soit différentiable et, en général, il ne l’est pas.
C’est d’ailleurs en exhibant une fonction ayant deux points critiques non dégénérés que Milnor démontre [4] qu’une certaine variété qu’il construit est homéomorphe à $\mathbf{S}^7$ sans pour autant lui être difféomorphe.

$$ $$

Franchissement de valeur critique

On s’intéresse maintenant au cas où $f^{-1}([a,b])$ contient un unique point critique. Cette fois-ci, comme on a pu le voir sur des exemples dans la théorie de Morse en mots et en images, $M^b$ n’est pas difféomorphe à $M^a$, mais à $M^a$ avec une anse attachée. Précisons cette notion. Pour tout $k\in\mathbb{N}$, on note $D^k$ le disque unité fermé de $\mathbb{R}^k$.

Remarque. Cette définition s’étend au cas où $W=\emptyset$, l’anse attachée étant alors nécessairement d’indice $0$ (de sorte que $\partial D^k\times D^{n-k}=\emptyset$), et le résultat de l’attachement étant alors simplement une boule de dimension $n$.

Avant de revenir à nos sous-niveaux, donnons quelques exemples (pour une introduction très visuelle à cette notion dans le cas de la dimension $3$, on pourra consulter l’article sur les scindements de Heegaard).

Un corps en anses de genre $g$ s’obtient à partir de la boule de dimension $3$ par attachement de $g$ anses d’indice $1$.

En attachant une $2$-anse à un tore plein le long d’un voisinage tubulaire d’une longitude, on obtient une variété homéomorphe à une boule.

En attachant une $3$-anse à une boule, on obtient une variété homéomorphe à la sphère de dimension $3$.

Remarques.

• La variété obtenue ne dépend en fait (toujours à homéomorphisme près) que de la restriction de l’application de recollement $\varphi$ à « l’âme » $\partial D^k\times\{0\}$ de la région de recollement $\partial D^k\times D^{n-k}$.
• Dans la suite, on se placera en fait dans le cadre différentiable, et on dira qu’une variété est obtenue à partir de $W$ par attachement d’une anse d’indice $k$ si elle est difféomorphe à la variété $W\cup_\varphi D^k\times D^{n-k}$ (pour un certain plongement $\varphi$), cette variété étant a priori seulement topologique mais possédant en fait une structure différentielle canonique obtenue en « lissant les coins ».

Nous sommes maintenant enfin en mesure d’énoncer le théorème sur le franchissement d’un point critique :

En termes homotopiques, il découle immédiatement que $M^b$ a le type d’homotopie de $M^a$ avec une $k$-cellule attachée (i.e. un disque de dimension $k$ recollé par un homéomorphisme de son bord dans $\partial M^a$). Ces énoncés se généralisent sans problème au cas où $f^{-1}([a,b])$ contient un unique niveau critique avec plusieurs points critiques, d’indices éventuellement différents.

Pour alléger les notations, supposons que la valeur critique en question est $0$, de sorte que $a < 0 < b$. Commençons par remarquer que d’après le premier théorème de cet article, il suffit de comparer $M^\epsilon$ et $M^{-\epsilon}$ pour $\epsilon$ aussi petit qu’on veut puisque $M^a$ est difféomorphe à $M^{-\epsilon}$ et $M^b$ à $M^{\epsilon}$, $f$ n’ayant pas de niveau critique autre que le niveau $0$ dans $f^{-1}([a,b])$.

Regardons à quoi ressemblent ces sous-niveaux dans le cas modèle (auquel on va se ramener grâce au Lemme de Morse) où $f$ est la fonction

$$(x_1,...,x_n) \in\mathbb{R}^n\mapsto -x_1^2-...-x_k^2+x_{k+1}^2+...+x_n^2, $$

ayant un seul point critique, l’origine, d’indice $k$. La figure suivante représente le cas $k=1$ en dimension $3$ (tronqués en $x_1=\pm2$ pour des questions de visibilité).

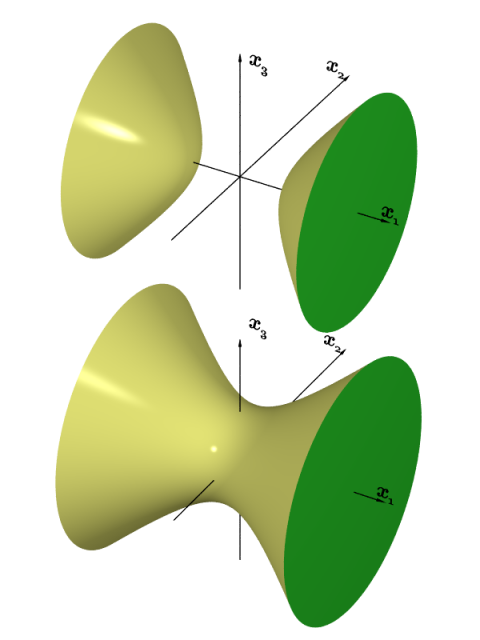
Posons $X=(x_1,...,x_k)$ et $Y=(x_{k+1},...,x_n)$. L’application

$$(X,Y)\mapsto \left(\tfrac{X}{\|X\|},f(X,Y)+\epsilon,Y\right)$$

induit un difféomorphisme entre $M^{-\epsilon}$ et $S^{k-1}\times \mathbb{R}_-\times \mathbb{R}^{n-k}$, représenté au début de l’animation située à la fin de la preuve, tandis que l’application

$$(X,Y)\mapsto \left(X,\tfrac{Y}{\sqrt{\epsilon+\|X\|^2}}\right)$$

induit un difféomorphisme entre $M^{\epsilon}$ et $\mathbb{R}^k\times D^{n-k}$, dont l’inverse est représenté à la fin de la même animation. Observons en outre que $\mathbb{R}_-\times \mathbb{R}^{n-k}$ est homéomorphe à $\mathbb{R}_-\times D^{n-k}$ via un homéomorphisme dont l’inverse est représenté dans le cas $n-k=2$ dans l’animation suivante.

Ainsi $S^{k-1}\times \mathbb{R}_-\times \mathbb{R}^{n-k}$ (et donc $M^{-\epsilon}$) est homéomorphe à $S^{k-1}\times \mathbb{R}_-\times D^{n-k}$. Considérons alors la variété obtenue en attachant à cette dernière une $k$-anse $D^k\times D^{n-k}$ par l’identification évidente de $\partial D^k\times D^{n-k}$ avec le sous-ensemble $S^{k-1}\times \{0\}\times D^{n-k}$ du bord de $S^{k-1}\times \mathbb{R}_-\times D^{n-k}$. Il s’agit du produit par $D^{n-k}$ du quotient de l’union disjointe $S^{k-1}\times \mathbb{R}_-\sqcup D^k$ par l’identification naturelle des deux bords, qui n’est autre que $\mathbb{R}^k$. On a ainsi montré que $M^{-\epsilon}$ avec une $k$-anse attachée était homéomorphe à $\mathbb{R}^k\times D^{n-k}$ et donc à $M^{\epsilon}$.

Les deux animations suivantes illustrent tout ceci dans les cas $(n,k)=(3,1)$ et $(3,2)$ respectivement. Dans la première, on regarde ce qui se passe en coupe dans le plan $(x_1,x_2)$. La version 3D s’obtient par symétrie de révolution autour de l’axe des $x_1$.

Dans la suivante, on se restreint au demi-espace $\{x_2\ge 0\}$. L’image complète s’obtient par symétrie par rapport au plan de l’écran, $\{x_2=0\}$.

Ceci conclut l’étude du cas modèle. Dans le cas général, « en gros », $M^{\epsilon}$ privé d’un voisinage du point critique (disons l’image inverse d’une boule par une carte donnée par le lemme de Morse) est homéomorphe à $M^{-\epsilon}$ privé de ce voisinage (l’homéomorphisme étant obtenu en poussant $M^\epsilon$ sur $M^{-\epsilon}$ le long des lignes de gradient descendant comme dans la partie précédente), et dans le voisinage « de Morse », on applique le cas modèle ci-dessus.