Le lemme de Morse

Dans la suite, nos variétés seront supposées lisses de classe $\mathcal{C}^{\infty}$ et nos fonctions infiniment différentiables.

Un point critique d’une fonction différentiable réelle $f$ définie sur une variété lisse $M$ de dimension $n$ est un point $x$ de la variété où la différentielle $Df(x)$ de $f$ en $x$ s’annule. La hessienne de $f$ en $x$

$$\begin{array}{ccccc} \text{Hess}(f) & : & T_xM \times T_xM & \longrightarrow & \mathbf{R} \\ & & (v,w) & \longmapsto & V\cdot(W\cdot f) \\ \end{array}$$

où $V$ et $W$ désignent deux champs de vecteurs définis localement au voisinage de $x$ tels que $V_x=v$ et $W_x=w$, est une forme bilinéaire symétrique. La symétrie est une conséquence du fait que $V_x\cdot W(f)-W_x\cdot V(f) = [V,W]_x(f) = 0$ puisque $x$ est un point critique, ce qui assure également le bien-fondé de la définition.

Nous dirons que $x$ est un point critique non dégénéré si la hessienne de $f$ en $x$ est non dégénérée (l’orthogonal de $T_xM$ pour cette forme est nul). L’indice de $f$ en $x$ désignera l’indice de la hessienne de $f$ en $x$, c’est-à-dire la dimension maximale d’un sous-espace vectoriel de $T_xM$ sur lequel elle est définie négative. Nous allons voir que le lemme de Morse énonce comment le comportement local de $f$ en $x$ est entièrement décrit par cet indice. Mais avant cela quelques exemples :

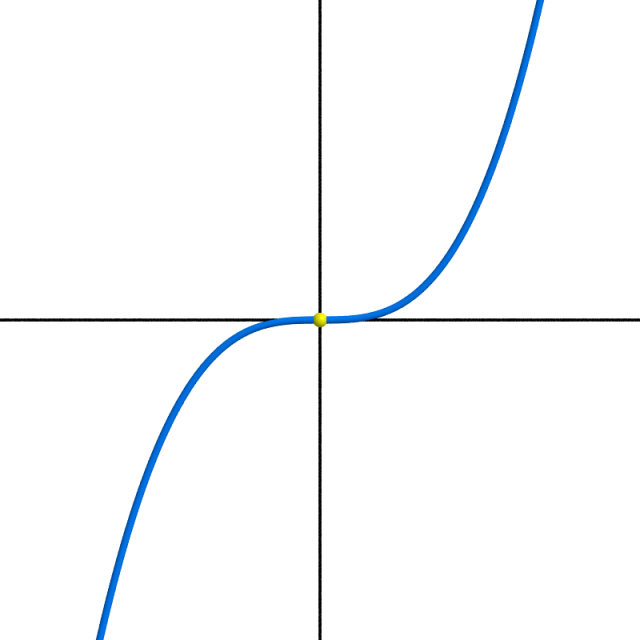
• L’origine $0$ est un point critique dégénéré (isolé) de la fonction $x \longmapsto x^3$.

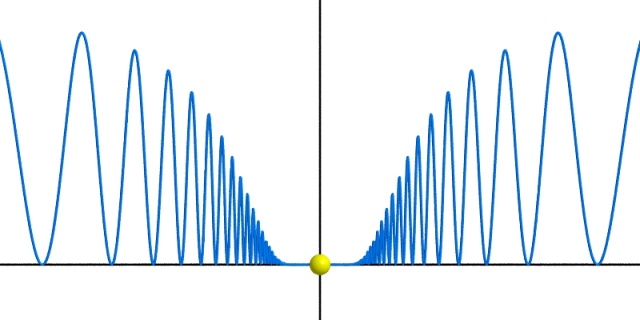
• L’origine $0$ est un point critique dégénéré non isolé de la fonction $x \longmapsto \text{e}^{-1/x^2} \text{sin}^2(1/x)$ [1].

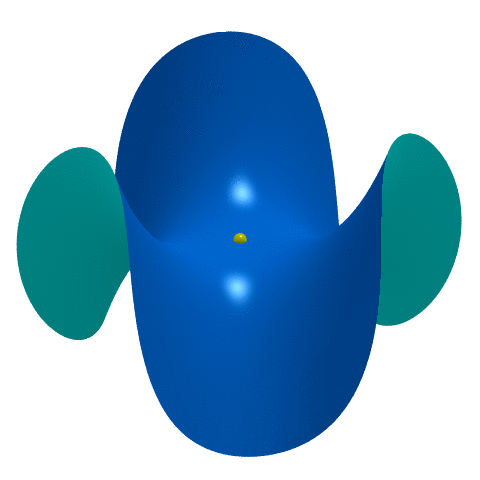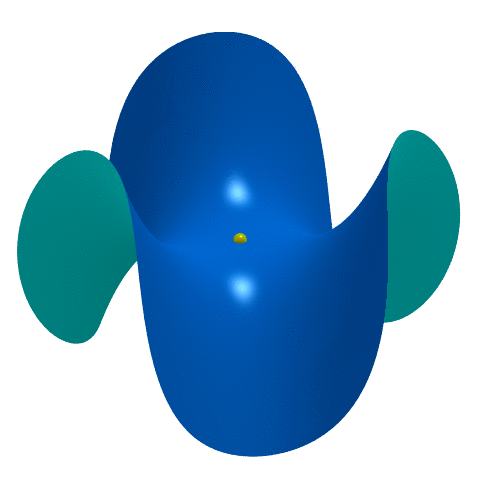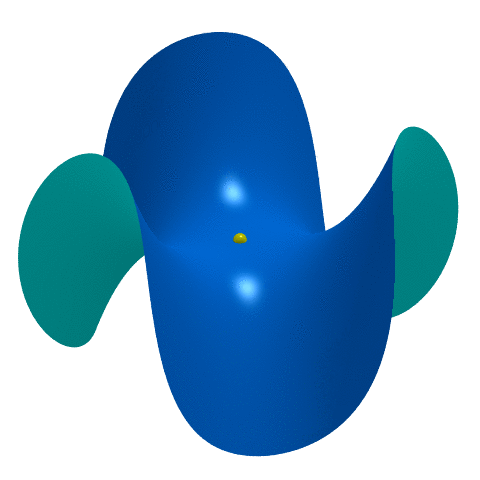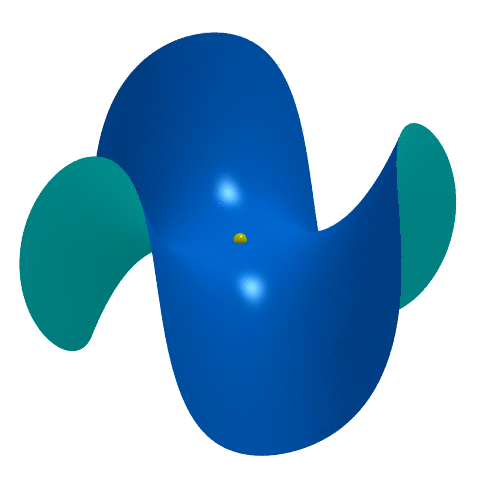
• L’origine $(0,0)$ est un point critique dégénéré de la selle de singe, c’est-à-dire de la fonction $(x,y) \longmapsto \text{Ré}(x+iy)^3 = x^3-3xy^2$.

• L’axe des $x$ est l’ensemble des points critiques de la fonction $(x,y) \longmapsto x^2$ : ils sont tous dégénérés.

• Dans le cas d’une fonction comme $(x,y) \longmapsto x^2 y^2$, les deux axes $x$ et $y$ forment l’ensemble des points critiques et ils sont également tous dégénérés.

Une fonction différentiable est dite de Morse si ses seuls points critiques sont non-dégénérés. C’est une conséquence immédiate du lemme précédent que les points critiques des fonctions de Morse sont des points isolés de la variété.

Nous allons consacrer la fin de ce paragraphe à la démonstration du lemme de Morse.
Commençons par remarquer que, dans un système de coordonnées locales $(x_1,\cdots,x_n)$ au voisinage du point critique $x$, on a $\frac{\partial f}{\partial x_i}(x) = 0$ pour tout $1 \leq i \leq n$.
Par ailleurs, la non-dégénérescence en $x$ revient à dire que la matrice $\left(\frac{\partial^2 f}{\partial x_i \partial x_j}\right)_{i,j}$ est inversible en $x$.
En effet, il résulte d’un calcul immédiat que si $v=\sum_i v_i \frac{\partial}{\partial x_i}(x)$ et $w=\sum_j w_j \frac{\partial}{\partial x_j}(x)$, alors

$$\text{Hess}(f)(x)=\sum_{i,j} v_i w_j \frac{\partial^2 f}{\partial x_i \partial x_j}(x).$$

Par suite, si $f$ admet une expression comme indiquée dans le lemme, la hessienne de $f$ en $x$ est une matrice diagonale ayant $\lambda$ coefficients $-2$ et $n-\lambda$ coefficients $2$, donc définie négative sur un sous-espace de dimension $\lambda$ et définie positive sur un sous-espace de dimension $n-\lambda$.
On en déduit donc que $\lambda$ est bien l’indice de $f$ en $x$.
Il nous reste donc à montrer l’existence d’un tel système de coordonnées.

Sans perte de généralité, on peut toujours trouver un système de coordonnées $(x_1,\cdots,x_n)$ tel que $x$, dans ce système de coordonnées, soit l’origine de $\mathbf{R}^n$, $f(x)=0$ et $f$ s’écrive

$$f(x_1,\cdots,x_n)=\sum_{j=1}^n x_j g_j(x_1,\cdots,x_n),$$

où les $g_i$ désignent des fonctions lisses telles que

$$g_j(0)=\frac{\partial f}{\partial x_j}(0)=0.$$

En effet, il suffit de poser

$$g_j(x_1,\cdots,x_n)=\int_{0}^1 \frac{\partial f}{\partial x_j}(tx_1,\cdots,tx_n)dt.$$

Le même raisonnement appliqué aux fonctions $g_j$ permet alors d’écrire

$$f(x_1,\cdots,x_n)=\sum_{j=1}^n x_i x_j h_{ij}(x_1,\cdots,x_n),$$

où les $h_{ij}$ désignent une certaine famille de fonctions lisses que l’on peut toujours supposer symétrique en $(i,j)$.
La non-dégénérescence de la hessienne de $f$ en $x$ revient à dire que la matrice dont les coefficients sont les $h_{ij}(0)$ est inversible.
On obtient l’expression cherchée pour $f$ par un changement de coordonnées obtenu par un raisonnement analogue à la diagonalisation des formes quadratiques.