Commentaires du troisième complément

Dans le troisième complément , Poincaré s’intéresse à la topologie des surfaces algébriques complexes définies par une équation du type

$$ z^2 = F(x,y) $$

où $F$ est un polynôme en deux variables [1]. Voici un extrait :

Voici maintenant la question qui se pose. M. Picard a démontré (cf. Théorie des fonctions algébriques de deux variables, t. I, p. 85 et suiv.) que, si une surface algébrique est la plus générale de son degré, les cycles linéaires peuvent être réduits à des points de telle façon que le nombre de Betti P1 est égal à 1. Il ne s’ensuit pas immédiatement que le groupe fondamental se réduise à la substitution identique. En effet, M. Picard a démontré que tout cycle linéaire est homologue à zéro, et, pour démontrer que le groupe fondamental se réduit à la substitution identique, il faudrait faire voir que tout cycle linéaire est équivalent à zéro.

Poincaré se propose ainsi de montrer que les surfaces $z^2 = F(x,y)$ sont simplement connexes. Sa démonstration comporte néanmoins une erreur sérieuse. Il n’empêche que, comme à son habitude, elle est truffée d’idées importantes. Et puis : l’énoncé s’avère être vrai ! Coup de chance ?

Revêtements doubles

Une difficulté inhérente à la lecture du troisième complément est le fait que Poincaré ne calcule pas le groupe fondamental de la surface affine $z^2=F(x,y)$ (c’est-à-dire l’ensemble des points $(x,y,z)$ de $\mathbb{C}^3$ qui satisfont cette équation), mais d’une compactification de cette surface dont il ne précise pas la définition.

La projection de surface affine $z^2=F(x,y)$ sur le plan des $(x,y)$ défini un revêtement double de ce plan ramifié le long de la courbe $F(x,y)=0$ [2]. Nous avons supposé que Poincaré choisit comme compactification le revêtement double du plan projectif $\mathbb P^2(\mathbb C)$ ramifié le long de la courbe dont l’équation affine est $F(x,y)=0$, que nous noterons $C$ [3]. Cela suppose notamment que le degré de $F$ soit pair. En effet, si $D$ est une droite générique de $\mathbb P^2(\mathbb C)$, la pré-image de $D$ par le revêtement double considéré ramifie aux points d’intersection de $D$ avec la courbe $C$, c’est à dire en exactement $d$ points, où $d$ est le degré de $F$. La formule de Riemann-Hurwitz nous dit que $d$ doit être pair.

Poincaré fait mention de la nécessité de cette condition [4] au milieu de son mémoire (alors qu’il n’avait initialement fait aucune hypothèse sur le polynôme $F$) :

Observons que l’on doit toujours réduire le degré de $F$ à être pair (au besoin par une transformation homographique), puisque le nombre des points singuliers est $2p+2$, (...)

Cette phrase indique non seulement que le degré de $F$ se doit d’être pair, mais aussi que l’on peut toujours se ramener à ce cas« par une transformation homographique ». Géométriquement, cela veut dire que, quitte à faire un changement de coordonnées projectif, l’on peut ajouter à la courbe de ramification $F(x,y) =0$ la droite à l’infini, de façon à rendre l’équation de degré pair. Cela faisant, on crée des points doubles ordinaires pour la courbe de ramification. C’est probablement cette raison qui amène Poincaré à considérer ce type de singularités. Nous ne commenterons pas plus le cas des courbes singulières dans ce qui suit, le cas des courbes lisses étant déjà suffisamment riche.

Remarquons qu’il n’est pas immédiat que la parité du degré de $F$ soit une condition suffisante pour l’existence d’un revêtement double ramifié [5]. Ce point n’est pas du tout discuté par Poincaré dans le Troisième complément.

Une formule pour le groupe fondamental

Dans un premier temps, Poincaré cherche à obtenir une description du groupe fondamental de la surface considérée. Sa technique consiste à "balayer" cette surface par un pinceau de courbes algébriques. Celles-ci sont obtenues en fixant simplement la valeur de la coordonnée $y$. Plus formellement, on considère le pinceau de courbes $(F_{y})_{y\in\mathbb{P}^1(\mathbb{C})}$ où $F_{y_0}$ est l’adhérence (dans la surface complexe considérée) de la courbe définie par l’équation $z^2 = F(x, y_0)$ dans $\mathbb{C}^3$. Si on note $D_{y_0}$ la droite de $\mathbb P ^2(\mathbb C)$ d’équation $(y=y_0)$, alors la courbe $F_{y}$ est lisse quand $D_{y}$ de $\mathbb P ^2(\mathbb C)$ intersecte transversalement la courbe de ramification $C$, et sinon elle est singulière. Quitte à remplacer la coordonnée $y$ par une combinaison linéaire générique des coordonnées $x$ et $y$, on peut supposer que la courbe $F_{y}$ n’est singulière que pour un nombre fini de valeurs de $y$, qu’elle ne présente alors qu’un seule point singulier, et que ce point singulier est un point double ordinaire (i.e. tel que la courbe est localement isomorphe à $v^2+w^2=0$ au voisinage de $(0,0)$ dans $\mathbb{C}^2$) [6]. Topologiquement, les courbes régulières du pinceaux sont des surfaces réelles lisses orientées fermées comme sur la figure ci-dessous à gauche. Par continuité, elles ont toutes le même genre. Les courbes singulières présentent, quant à elles, un noeud comme sur la figure ci-dessous à droite.

Intéressons-nous à une valeur critique $y_c$, c’est-à-dire une valeur $y_c$ telle que la droite $D_{y_c}$ soit tangente à la courbe de ramification $C$. Quand $y$ s’approche de $y_c$, une certaine courbe fermée simple (réelle) contenue dans la courbe (complexe) $F_y$ sera pincée sur le noeud de la courbe singulière $F_{y_c}$, comme représenté sur la figure ci-dessous. En effet, lors de cette déformation, deux des points d’intersection transverse de la droite $D_{y}$ avec la courbe $C$ vont coalescer vers le point de tangence de $D_{y_c}$ avec $C$. Si on considère un petit arc joignant ces deux points dans $D_{y}$, alors la pré-image de cet arc dans le revêtement double est une courbe fermée simple sur $F_y$, qui sera pince vers le noeud de la courbe singulière $F_{y_c}$ quand $y$ s’approche $y_c$. Les courbes fermées simples « disparaissent » de cette manière s’appellent des cycles évanescents.

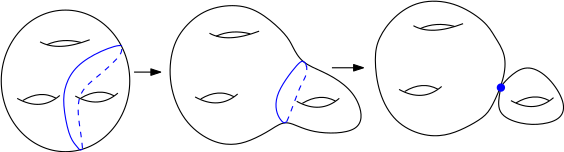
Déformation d’une fibre régulière en une fibre singulière. En bleu, le cycle évanescent qui dégénère sur un point double ordinaire.

Fixons maintenant une courbe régulière $F_{0}$ dans le pinceau, et dessinons la collection des cycles évanescents correspondant à des déformations de $F_{0}$ vers chacune des fibres singulières du pinceau. Un énoncé absolument fondamental de ce troisième complément est une formule pour le groupe fondamental de la surface complexe considérée, en termes de la donnée des cycles évanescents. Il s’agit du précurseur du théorème de la section hyperplane de Lefschetz, et s’énonce ainsi

Commentons la démonstration que Poincaré donne de ce résultat, et qui constitue la partie la plus importante du troisième complément. Il commence par calculer le groupe fondamental de la surface complexe privée des fibres singulières du pinceau, que nous appellerons la partie régulière du pinceau par la suite. Il est tout à fait remarquable qu’il construit de façon explicite le revêtement universel de la partie régulière, ainsi que l’action du groupe de revêtement, à l’aide de fonctions multiformes. L’argument utilise de façon cruciale la théorie des fonctions fuchsiennes, qu’il avait développée entre 1881 et 1884. L’usage de ces fonctions lui permet de construire un modèle pour le revêtement universel, qui est un difféomorphe au produit de deux disques de $\mathbb{C}$). De plus, l’action du groupe fondamental est alors donnée par des transformations de la forme

$$ (x,y) \mapsto \left( \frac{A(y) x + B(y)}{C(y) x + D(y) } , \frac{\alpha y + \beta}{\gamma y + \delta} \right) $$

À $y_0$ fixé, le groupe engendré par les transformations $x\mapsto \frac{A(y_0) x + B(y_0)}{C(y_0) x + D(y_0) }$ est un groupe fuchsien cocompact qui uniformise la compactification de la courbe $z^2 = F(x,y_0)$.

Attention, les fonctions $A,B,C,D$ ne sont pas des fonctions holomorphes de la variable $y$ mais seulement continues (et même différentiables).

Le groupe engendré par les transformations $y \mapsto \frac{\alpha y + \beta}{\gamma y + \delta}$ est le groupe fuchsien non cocompact qui uniformise la sphère de Riemann $\mathbb{P}^1(\mathbb{C})$ privée des valeurs critiques du pinceau (i.e. des points $y_0\in \mathbb{P}^1(\mathbb{C})$ pour lesquelles la droite $D_{y_0}$ présente une tangence avec la courbe $F(x,y)=0$). Poincaré déduit alors que le groupe fondamental de la partie régulière est un produit semi-direct du groupe fondamental de la sphère de Riemann privée des valeurs critiques, par le groupe fondamental d’une courbe régulière du pinceau.

Notons que le pinceau de courbes $(F_{y})_{y\in \mathbb{P}^1(\mathbb{C})}$ possède deux points bases [7] par lesquels passent toutes les courbes du pinceaux. Poincaré raisonne comme si ces points bases n’existaient pas, i.e. comme si les courbes du pinceaux étaient deux à deux disjointes. Autrement dit, la variété dont il calcule le groupe fondamental n’est pas exactement le revêtement double ramifié de $\mathbb{P}^2(\mathbb{C})$ évoqué précédemment, mais plutôt son éclaté aux points bases du pinceau [8]. On sait bien qu’un éclatement n’affecte pas le groupe fondamental [9], mais on notera qu’aucune remarque à ce propos n’apparaît dans le troisième complément.

Une fois que Poincaré a étudié le groupe fondamental de la partie régulière, il lui reste à étudier ce qui se passe lorsqu’on « ajoute » les fibres singulières. Il entreprend pour cela le calcul de la monodromie autour des fibres singulières, qu’il effectue dans les cas de genre $1$ et $2$, mais qui se généralise immédiatement au cas général. En termes modernes, ce résultat se formule ainsi

On attribue généralement ce résultat à Picard (cas homologique), et à Lefschetz (cas général des fibrations de Lefschetz). On trouvera dans cet article une définition précise des termes utilisés et une preuve du résultat dans le cadre général des fibration des Lefschetz. La démonstration de Poincaré est tout à fait explicite et utilise la nature hyperelliptique des courbes du pinceau. Cette démonstration est esquissée dans la vidéo ci-dessous, qui reprend également la description des surfaces complexes considérées par Poincaré, du pinceau utilisé, et des cycles évanescents.

Fort de cette formule, Poincaré prouve (en utilisant sans le démontrer le théorème de Van Kampen) que le fait d’ajouter une fibre singulière crée une relation supplémentaire et une seule : celle donnée par le cycle évanescent. Il obtient ainsi le théorème annoncé.

L’erreur de Poincaré

À ce stade, on sait donc que le groupe fondamental de la surface complexe considérée est le quotient du groupe fondamental de la courbe $F_0$ par le sous-groupe normal engendré par les cycles évanescents de $F_0$. Poincaré se propose alors de montrer qu’il existe suffisamment de cycles évanescents dans une courbe $F_0$ donnée pour « tuer » le groupe fondamental de $F_0$.

Rappelons comment apparaissent ces cycles évanescents. Quand $y$ tend vers une valeur singulière $y_c$, deux des points d’intersection transverses de la droite $D_y$ avec la courbe de ramification $C$ vont coalescer vers le point de tangence de la droite $D_{y_c}$ avec $C$. Dans la droite $D_0$, cette coelescence définit un arc plongé reliant ces deux points et ne passant pas par les autres points d’intersection avec la courbe de ramification. La préimage d’un tel arc dans $F_0$ est un cycle évanescent.

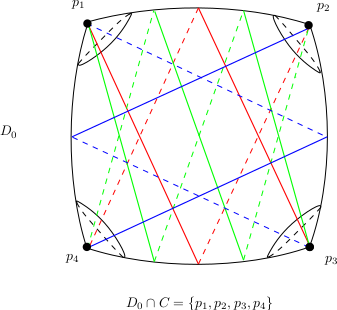
On peut alors tracer tous les arcs obtenus de cette façon entre certaines paires de points d’intersection de $D_0$ avec la courbe de ramification, pour obtenir ce que nous appelons un "système d’arc". Poincaré affirme que toute paire de points de $D_0 \cap C$ sont les extrémités d’un certain arc de ce système. Ceci découle du fait que le groupe de monodromie de la fonction définie implicitement par $F(x, y(x) ) = 0$ est le groupe symétrique en $d$ lettres tout entier. Poincaré conclut en affirmant que cette condition suffit pour assurer que les pré-images de ces arcs dans la courbe $F_0$ (rappelons que $F_0$ est le revêtement double de $D_0$ ramifié sur $D_0 \cap C$) engendre le groupe fondamental de cette dernière. Or cette affirmation est fausse, comme le montre le système d’arc dessiné sur la figure.

En effet, dans ce cas, le revêtement double de $D_0$ aux quatre points $p_1,p_2,p_3,p_4$ d’intersection de $D_0$ avec $C$ est un tore, et le quotient du groupe fondamental de ce dernier par les pré-images des arcs de ce système est isomorphe à $(\mathbb Z/ 3\mathbb Z)^2$. Plus d’explications se trouvent dans cette video :

Comment « réparer » la démonstration ?

Comme nous l’avons déjà dit, le résultat annoncé par Poincaré n’en est pas moins vrai : les surfaces complexes obtenues comme revêtements doubles de $\mathbb{P}^2(\mathbb{C})$ ramifiés le long d’une courbe algébrique sont simplement connexes. Nous proposons ici une démonstration de ce résultat. Celle-ci suit aussi longtemps que possible la stratégie imaginée par Poincaré. La principale différence est que, plutôt que d’étudier les systèmes d’arcs dans le cas général, on se ramène à un cas particulier. En effet, la connexité de l’espace des courbes algébriques lisses de degré donné implique que la topologie des revêtements doubles considérés ne dépend que du degré du polynôme $F$. Il suffit alors de trouver, pour chaque degré $d$, un polynôme $F$ pour lequel on réussit à déterminer "à la main" un système d’arcs tel que les relevés de ces arcs engendrent le groupe fondamental d’une courbe régulière du pinceau. C’est ce que nous faisons.