Commentaires sur le §VII du premier complément

Dans ce paragraphe Poincaré construit un polyèdre dual $P'$ associé à un polyèdre $P$. Rappelons qu’un tel polyèdre est une variété compacte munie d’une cellulation lisse, voir Commentaire du §II. Par ailleurs, Poincaré suppose depuis le §II que ses variétés sont sans bord. Ce polyèdre dual est obtenu comme une nouvelle décomposition polyédrale de la réalisation du polyèdre $P$. Il conviendra de noter que même lorsque $P$ est un complexe simplicial, la cellulation duale ne donne pas un complexe simplicial mais bien un polyèdre au sens moderne (ou un CW-complexe).

La construction de $P'$ est une généralisation de l’idée du dual d’un polyèdre convexe, dans le cadre des variétés sans bord, et est purement intrinsèque à la variété polyédrale $P$ elle même. Elle ne fait pas appel à la géométrie de l’espace ambiant dans lequel $P$ est plongé.

La construction de Poincaré est donnée pour un polyèdre de dimension 3 plongé dans l’espace à 4 dimensions, mais se généralise [1] au cas général d’un polyèdre de dimension $n$ plongé dans un espace de dimension $m$.

La construction de Poincaré commence par regarder le polyèdre dérivé de $P$. Ce polyèdre est construit inductivement en subdivisant les cellules de $P$ de la manière suivante : si on a subdivisé les cellules de dimension $p$, une cellule de dimension $p+1$ est subdivisée en prenant un point intérieur et en considérant les cônes en ce point de base les cellules de la subdivision de son bord. Bien entendu, cette construction de Poincaré dépend de choix, mais tout choix est PL-isomorphe à celui obtenu en prenant les barycentres de chaque simplexe (c’est à dire la subdivision barycentrique). On peut noter que le polyèdre dérivé de n’importe quel complexe polyédral est un complexe simplicial.

Une fois fixé ce polyèdre dérivé, Poincaré construit la cellulation $P'$. Le résultat établi par Poincaré dans ce paragraphe est

La deuxième partie de ce résultat est en fait un cas particulier du théorème d’invariance par subdivision du §V dans le cas polyédral. En effet, les deux cellulations ont toutes les deux le polyèdre dérivé de $P$ comme subdivision. On a d’ailleurs pas besoin du théorème pour des subdivisions arbitraires mais seulement pour des subdivisions stellaires, c’est à dire obtenue en ne rajoutant qu’un point dans une seule cellule, puisque la subdivision barycentrique s’obtient par une suite finie de telles subdivisions à partir à la fois de $P$ et $P'$, c’est un cas beaucoup plus facile qui se rapproche de l’invariance par collapse. Cependant, étonnamment, Poincaré ne signale cette approche que dans une phrase rapide à la fin de ce paragraphe après une démonstration directe et un peu laborieuse consistant à déformer des chaînes de la triangulation $P$ vers celles de la triangulation $P'$. Cette démonstration a cependant le mérite d’introduire certaines remarques fondamentales pour la suite comme nous allons le voir.

Poincaré définit la cellulation duale comme suit : à une cellule de dimension $3-r$, notée $a_i^{3-r}$ on associe une cellule de dimension $r$, notée $b_i^r$ définie inductivement par $b_i^0$ est le barycentre de $a_i^3$ et, pour $r\geq 1$, $b_i^r$ est le cône de centre le barycentre de $a_i^{3-r}$ et de base la réunion de toutes les cellules $b_j^s$ [2] de $P$ dont les cellules correspondantes $a_j^{3-s}$ contiennent $a_i^{3-r}$ dans leur bord, ceci se généralise en toute dimension. Le fait que les $b_j^s$ forment bien des $s$-cellules est équivalent au fait que les liens des cellules $a_j^{3-s}$ soient des sphères de dimension $r-1$, autrement dit que la variété $M$ est munie d’une structure $PL$ (et sans bord). Poincaré énonce ce fait sans s’étendre sur la démonstration. Bien entendu, cette construction dépend de la structure $PL$ a priori, mais Poincaré ignore les subtilités concernant l’existence et la classification de ces structures et travaille dans un cadre différentiable pour lequel on peut trouver un choix canonique de cellulation duale bien que ces résultats (et même la problématique qui les ont soulevés) soient très postérieurs à l’Analysis Situs.

Afin de démontrer "directement" l’égalité des nombres de Betti réduits de $P$ et $P'$ Poincaré fait deux remarques fondamentales. La première est que si la variété est orientée, alors l’orientation des cellules $a_i^r$ de $P$ induit une orientation canonique des cellules de $P'$. Elle est définie par la condition que l’orientation de $P$ doit correspondre à l’orientation obtenue en prenant le produit $a_i^{r} \times b_{i}^{3-r}$ (on peut remarquer que ces cellules sont transverses dans $P$).

La deuxième observation (qui découle entre autre de cette première) est que, munie de l’orientation induite, les relations d’incidence de $P$ sont inversées par rapport à celles de $P'$ ; autrement dit $a_i^{r}$ est une face de $a_j^{s}$ si et seulement si $b_j^{3-s}$ est une face de $b_i^{3-r}$. On a en fait le lemme suivant [3] :

En termes moderne de complexe de chaînes, ce lemme signifie qu’il y a un accouplement non-dégénéré entre les complexes cellulaires de $C_{i}(P')$ et $C_{4-i}(P)$ qui identifie $C_{4-i}(P')$ avec le complexe de cochaînes dual de $C_{*}(P)$. C’est à dire que le dual du morphisme de bord

$$\partial: C_i(P) \to C_{i-1}(P)$$

est le cobord

$$\delta : C^{3-i}(P') \to C^{4-i}(P')$$

où $C^q(P')= \mathrm{Hom}(C_p(P'), \mathbb{Q})$ et $\delta (f)= f\circ \partial$ au signe près.

De là on peut déduire immédiatement le résultat principal sur les nombres de Betti via le théorème des coefficients universels dont les techniques ne sont évidemment pas du tout contemporaines de Poincaré. Dans les parties suivantes, il va démontrer ce résultat par des manipulations arithmétiques et d’algèbre linéaire.

Commentaire sur la démonstration élémentaire et directe de $b_1(P)=b_1(P')$.

Expliquons la stratégie de Poincaré dans ce degré. Il convient de montrer que $b_1(P')\leq b_1(P)$ et $b_1(P)\leq b_1(P')$. Soit alors $\sum b_i^1$ un cycle de $P'$. En se rappelant que Poincaré ne demande pas que les homologies soient cellulaires dans sa définition des nombres de Betti réduits, il suffit de montrer que ce cycle est homologue à un cycle de $P$. On commence par remarquer que, par définition de $b_i^1$ comme étant la réunion de 2 arêtes de la subdivision barycentrique de $P$ issues d’un même barycentre d’une 2 face et pointant vers le barycentre de deux 3 cellules ayant cette face dans leur bord, un tel cycle se réécrit comme une somme de chemins fermés formés de cellules $c_i^1$ où $c_i^1$ désigne la concaténation de deux arêtes de la subdivision barycentrique partant d’un même barycentre d’une 3-cellule et aboutissant sur le barycentre de deux de ses faces (distinctes) ; en particulier chaque $c_i^1$ vit dans une unique 3-cellule. L’intérêt de cette réécriture est que, comme les 3-cellules sont contractiles, chaque $c_*^1$ est homologue à $d_*^s- d_*^b+\sum a_k^1$ où $a_k^1$ est une arête de $P$ (et plus précisément de la 3-cellule $a^3_*$ dans laquelle $c_*^1$ vit), $d_*^s$ est une arête de la subdivision barycentrique reliant le barycentre de la 2-face d’où $c_*^i$ est issue à un sommet de $P$ et $d_*^b$ est une arête de la subdivision barycentrique reliant le barycentre de la 2-face où $c_*^i$ aboutit à un sommet de $P$. On peut choisir itérativement les $d_*^s$ et $d_*^b$ de manière cohérente (puisque on a un cycle) ; c’est à dire que une fois choisi $d_*^b$ l’arête correspondant au barycentre de la 2-face où $c_*^1$ aboutit, alors on choisit le $d_{*+1}^s=d_*^{b}$ pour l’arête suivante $c_{*+1}$.

En sommant toutes les homologies, les $d_*^{s,b}$ s’annulent deux à deux et on obtient bien que $\sum b_i^1$ est homologue à $\sum a_k^1 $ qui est un 1-cycle de $P$.

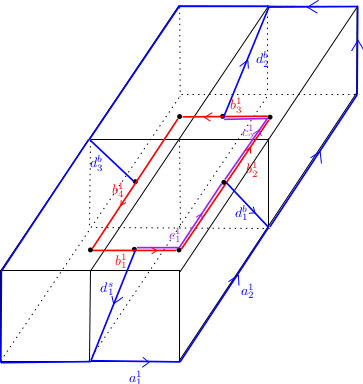
Pour démontrer l’inégalité inverse, on part d’un cycle $\sum a_j^1$. Pour chaque $a_j^1$, on peut choisit une 3-cellule $a_*^3$ qui la contient, 2 faces de cette 3-cellules qui contiennent aussi $a_j^1$. On a alors, comme précédemment, $c_*^1$ la concaténation des 2 arêtes de la subdivision barycentrique reliant les barycentres des faces choisies au barycentre de $a_*^3$. Par contractibilité des cellules, l’arête $a_j^1$ est homologue à $d_*^s- d_*^b+ c_*^1$ où $d_*^s$, $d_*^b$ sont les arêtes reliant le barycentre des cellules choisies de dimension $2$ avec les sommets respectifs de $a_j^1$. On peut voir de plus que $d_{*}^{b} - d_{*+1}^{s}$ est homologue à une somme (précisément deux) de chemin du type $c_k^1$ (ce qui évite d’avoir à les choisir convenablement pour qu’ils se simplifient).

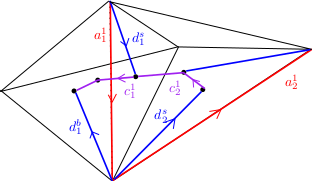
En sommant toutes ces homologies on obtient alors que $\sum a_j^1$ est homologue à un cycle de la forme $\sum c_k^1$. Comme précédemment un tel cycle se réécrit comme une somme de $\sum b_l^1$ (en "translatant" juste le sommet de départ des chemins), donc comme un cycle de $P'$. Ce qui termine de montrer $b_1(P)\leq b_1(P')$.

Cette idée se généralise en toute dimension et est essentiellement la preuve de Poincaré. Elle utilise évidemment de manière cruciale que Poincaré s’autorise de prendre des bords (et donc des relations d’homologie) non-cellulaires.
Poincaré revient encore sur cette démonstration dans le §X, d’une manière cette fois-ci plus algébrique ; en particulier sans faire ce choix de quotienter par toutes les homologies. En dehors de l’aspect éventuellement plus rigoureux, Poincaré notera surtout que cette démonstration algébrique aura du sens pour des objets obtenus en recollant des cellules mais qui ne sont pas nécessairement des variétés, à condition qu’ils vérifient certaines propriétés d’incidence entre cellules et cellules duales.

Dernière remarque :
Que les nombres de Betti (réduits) de $P$ et $P'$ soient les mêmes découle aussi bien sûr du théorème d’invariance de l’homologie d’un espace par rapport à une décomposition cellulaire autour duquel Poincaré ne cesse de revenir. En fait, Poincaré suggère que l’on peut même démontrer l’invariance en utilisant le théorème précédent pour une triangulation particulière et des choix judicieux de points au sein des 3 cellules de $P$, mais sans donner de détails convaincants.