Commentaires sur le §3 de l’Analysis Situs (Deuxième définition des variétés)

Dans le §3, Poincaré échafaude une « deuxième définition des variétés », plus générale que celle qu’il a proposée au §1. Cette deuxième définition utilise des paramétrages locaux et un principe de prolongement analytique.

Variétés élémentaires

Poincaré commence par construire un type particulier de variétés à $m$ dimensions, que nous appellerons variétés élémentaires.

Poincaré affirme alors qu’il est clair qu’une telle variété élémentaire est une variété à $m$ dimensions au sens de son §1. Telle quelle, cette affirmation est fausse. En effet, considérons la courbe dessinée ci-dessous en rouge :

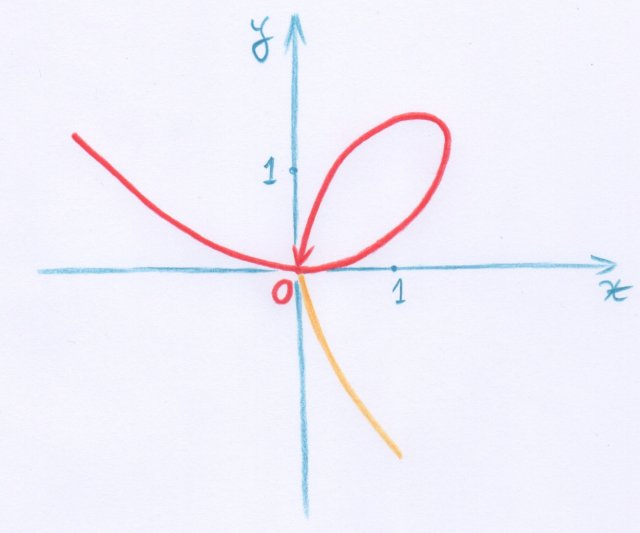
Il s’agit de la portion du folium de Descartes, d’équation cartesienne $x^3 + y^3 = 3xy$, qui peut être paramétrée par :

$$\begin{array}{ccc} ]-1 , + \infty[ & \mapsto & \mathbb{R}^2 \\ t & \mapsto & \left(\dfrac{3t}{1 + t^3}, \dfrac{3t^2}{1 + t^3} \right) \end{array} . $$

Cette courbe $V$ peut donc être décrite comme l’image d’une application $y\mapsto(\theta_1(y),\theta_2(y))$ de $]-1 , + \infty[$ dans $\mathbb{R}^2$, dont la matrice jacobienne est partout de rang $1$, mais n’est pas une variété à $1$ dimension au sens de la première définition de Poincaré. En effet, si tel était le cas, alors d’après le théorème des fonctions implicites, il existerait un voisinage $U$ de $O$ dans $\mathbb{R}^2$ tel que $V\cap U$ soit un graphe $y=f(x)$, ou bien un graphe $x=g(y)$, avec $f$ et $g$ lisses. La situation locale au voisinage du point $O$ étant différente, la portion rouge du folium n’est pas une variété au sens de la première définition de Poincaré.

L’affirmation de Poincaré devient correcte si l’on ajoute une hypothèse de propreté de l’application $(y_1,\dots,y_m)\mapsto (\theta_1(y_1,\dots,y_m),\dots,\theta_n(y_1,\dots,y_m))$, mais la preuve n’est pas tout à fait aussi simple que semble le penser Poincaré (il faut montrer qu’une immersion injective et propre est un difféomorphisme sur son image, puis utiliser un voisinage tubulaire).

On notera par ailleurs que le début du §3 est écrit dans un style narratif assez informel :

• Poincaré ne fait tout d’abord aucune hypothèse sur le rang de la matrice jacobienne de l’application $\theta$. L’ensemble $V:=\theta(U)$ n’a alors aucune raison d’être une variété à $m$ dimensions (il peut par exemple être réduit à un point). Ce n’est que quelques lignes plus bas que Poincaré écrit qu’il supposera toujours que la matrice jacobienne de l’application $\theta$ est de rang $m$.

• Poincaré oublie également de demander l’injectivité de l’application $\theta$. Cette hypothèse est néanmoins tacite, puisqu’il prendra soin de la vérifier à la fin du §3, lorsqu’il montrera que toute variété au sens de sa première définition est également une variété au sens de sa deuxième définition.

Seconde définition des variétés par Poincaré

Poincaré propose alors de généraliser la notion de variété, en en définissant de nouvelles par recollement de variétés élémentaires. Pour cela il se propose d’utiliser un principe de prolongement analytique.

Il commence par affirmer que, si $V$ est une variété élementaire donnée par une immersion $\theta$, il pourra sans perte de généralité supposer que $\theta$ est analytique. Pour justifier cela, il explique que, quand bien même $\theta$ ne serait pas analytique, il pourrait la remplacer par une application $\theta'$ analytique, « aussi proche » de $\theta$ qu’on voudra (Poincaré ne précise pas à quelle notion de proximité il fait référence). Sous-jacent à ce raisonnement, il y a deux implicites :

• le fait que deux variétés difféomorphes sont considérées comme équivalentes (voir le §2 et ses commentaires) ;
• l’affirmation tacite que deux variétés élémentaires suffisamment « proches » sont difféomorphes. Cette affirmation est vraie, pour peu que les variétés soient « proches » au sens de la topologie $C^1$ (de Whitney s’il s’agit de variété non-compactes).

Cette définition est proche de la définition moderne des sous-variétés de $\mathbb{R}^n$ par paramétrage local (voir nos commentaires du §1.). En fait, toute sous-variété analytique de $\mathbb{R}^n$ au sens moderne est clairement une variété au sens de la (seconde) définition de Poincaré. La réciproque est fausse : en effet, Poincaré autorise $V_i$ à intersecter $V_j$ le long d’un ensemble discret. Ainsi un « huit » dans $\mathbb{R}^2$ est une variété au sens de Poincaré, mais pas une sous-variété au sens moderne. En fait, la définition de Poincaré correspond à ce qu’on appelle de nos jours une variété (analytique) immergée irréductible.

L’irréductibilité provient de son hypothèse de pouvoir relier deux quelconques des variétés élémentaires $V_i$ par une chaîne de variétés élémentaires dont les intersections successives soient ouvertes et non-vides. Par exemple, l’union des axes de coordonnées dans $\mathbb{R}^2$ n’est pas une variété au sens de la deuxième définition de Poincaré.

Pourquoi se restreindre à des paramétrages analytiques ?

Les notions modernes de sous-variété utilisent des caractérisations locales, et fonctionnent parfaitement dans la catégorie lisse (et même topologique). Pourtant, quand Poincaré veut passer d’une définition globale des variétés (au §1) à une définition locale (au §3), il doit se placer dans la catégorie analytique pour faire des recollements. Pourquoi cela ?

Probablement parce que nos définitions modernes reposent fondamentalement sur la notion de voisinage. À l’époque où écrit Poincaré, l’édifice de la topologie générale n’avait pas encore été construit. Bien sûr, l’expression « au voisinage d’un point $x$ de $\mathbb{R}^n$ » n’aurait certainement pas surpris Poincaré, et il en aurait sans aucun doute parfaitement compris le sens. Il n’empêche que la notion de voisinage n’avait pas encore émergé. Imaginer une définition du type « On dira que $V$ est une variété si tout point $x$ de $V$ admet un voisinage tel que... » chez Poincaré est donc un anachronisme. Par contre, le principe de prolongement analytique était parfaitement familier à Poincaré qui avait tant réfléchi aux surfaces de Riemann et à leur uniformisation.

Lien entre la première et la seconde définition des variétés par Poincaré

Poincaré montre que toute variété (supposée tacitement analytique) au sens de sa première définition est aussi un variété au sens de sa seconde définition. Pour ce faire, il applique simplement le théorème des fonctions implicites. Puis il annonce qu’il donnera plus tard (voir les commentaires du §8) des exemples de parties de $\mathbb{R}^n$ qui sont des variétés selon sa seconde définition mais pas la première. La seconde définition est donc strictement plus générale que la première. La raison principale de cette différence a déjà été évoquée plus haut : une partie de $\mathbb{R}^n$ qui satisfait la première définition de Poincaré est une sous-variété définie par un système d’équations globales ; l’existence de ces équations globales implique des propriétés globales de cette sous-variété ; par exemple, son fibré normal est trivial, et en particulier, elle est orientable ; la seconde définition de Poincaré étant locale, elle n’implique aucune propriété globale de ce type.

Pourquoi des équations globales et des paramétrages locaux ?

Le lecteur moderne, habitué à jouer avec les trois définitions équivalentes de sous-variété rappelées dans nos commentaires du §1, pourra être surpris par les définitions introduites par Poincaré. Pourquoi une première définition par équations globales et une seconde définition par paramétrage local ? Pourquoi ne pas proposer une définition par équations locales ?

D’une part, il évident que les définitions de Poincaré proviennent de la théorie des variétés algébriques. Poincaré a dit explicitement dans son introduction que l’étude (de la topologie) des surfaces algébriques est l’une de ses prinicipales motivations ; il y consacrera les troisième et quatrième compléments de l’Analysis Situs. Les variétés algébriques sont naturellement données par des équations (polynomiales) globales. Bien sûr, on peut les paramétrer localement, en les voyant localement comme des graphes grâce au théorème des fonctions implicites. Pour une courbe algébrique, le théorème d’uniformisation [1] fournit un paramétrage global (non-injectif). Mais Poincaré pense certainement qu’il n’existe pas d’espoir de généraliser le théorème d’uniformisation aux variétés algébriques de toutes dimensions (ni même aux surfaces algébriques). Il faut donc se contenter de paramétrages locaux, ce qui explique la deuxième définition donnée par Poincaré. Notons que c’est peut-être par analogie avec le théorème d’uniformisation que Poincaré ne suppose pas l’injectivité de ses paramétrage locaux.

D’autre part, on a vu que, dans sa deuxième définition, Poincaré utilise un principe de prolongement analytique pour recoller les paramétrages locaux. Si, suivant le même principe, on recolle des équations locales par prolongement analytique, alors on obtient un seul système d’équations globales, exactement comme dans la première définition proposée par Poincaré. Le principe « pour définir globalement un objet, il suffit de le définir au voisinage de chacun de ses points » découle d’un point de vue qui, semble-t-il, ne deviendra naturel qu’au début du XXème siècle avec l’émergence de la topologie générale.