|
> Surfaces complexes > Simple connexité des revêtements doubles ramifiés du plan projectif (...) Simple connexité des revêtements doubles ramifiés du plan projectif complexe |
Dans cet article, nous montrons (comme Poincaré se proposait de le faire dans le Troisième Complément à l’Analysis Situs) que les surfaces algébriques complexes obtenues comme revêtements doubles ramifiés du plan projectif sont simplement connexe.
Rappelons que si l’on se donne une famille de $d= 2k$ points $x_1,\ldots, x_d$ de la droite projective complexe $\mathbb P^1(\mathbb C)$, il existe un unique revêtement double de $\mathbb P^1(\mathbb C)$ qui ramifie en chacun des points de cette famille. Nous renvoyons à Revêtements ramifiés entre surfaces. L’espace total de ce revêtement est alors une surface de Riemann dite « hyperelliptique », isomorphe à la courbe algébrique plane
$$ y^2 = (x - x_1) \ldots (x-x_d) $$
à laquelle on a ajouté deux points à l’infini. Le genre de cette courbe est égal à $g = k-1$. Le théorème de classification des surfaces compactes orientées (voir ici) indique qu’une surface fermée est caractérisée à homéomorphisme près par son genre. Ainsi, en considérant des revêtements doubles de $\mathbb P^1(\mathbb C)$ qui ramifient en $2k$ points, on obtient toutes les topologies possibles pour des courbes algébriques complexes.
Revêtements doubles ramifiés de $\mathbb P^2(\mathbb C)$
Dans le Troisième Complément à l’Analysis Situs, Poincaré s’intéresse aux surfaces complexes obtenues par une construction analogue. Soit $C$ une courbe algébrique lisse de degré pair $d= 2k $ dans $\mathbb P^2 (\mathbb C)$. La classe fondamentale de $C$ est donc un multiple pair de la classe d’homologie induite par une droite complexe dans $\mathbb P^2 (\mathbb C)$ (voir ici). Ceci implique qu’il existe un (en fait, unique) revêtement double $r : X \rightarrow \mathbb P^2(\mathbb C)$ de $\mathbb P^2(\mathbb C)$ qui est ramifié le long de $C$. Ce fait n’est pas trivial ; nous renvoyons au bloc Revêtements ramifiés (cas général) où le lecteur trouvera une démonstration de l’existence et de l’unicité. Observez que la parité de $d$ est nécessaire ici pour l’existence du revêtement double ramifié le long de $C$. En effet, un tel revêtement induit par restriction un revêtement double au-dessus de n’importe quelle droite projective complexe, qui ramifie sur exactement $d$ points, si la droite est choisie transverse à $C$. La formule de Riemann-Hurwitz donne la parité de $d$.
Si $P(x,y,z)= 0$ est une équation homogène de $C$, alors $X$ est l’hypersurface définie par $ t^2 = P(x,y,z) $ dans la $3$-variété
$$ (\mathbb C ^3 \setminus 0 )\times \mathbb C / (x,y,z,t) \sim (\lambda x, \lambda y , \lambda z, \lambda ^k t). $$
L’application de revêtement est définie par
$$[x:y:z:t]\in X \mapsto [x:y:z] \in \mathbb P^2(\mathbb C) $$
Chaque point de $\mathbb P^2(\mathbb C)$ admet deux préimages, sauf les points de $C$ qui en ont une seule : $X$ est donc bien un revêtement double de $\mathbb P^2(\mathbb C)$ ramifié le long de $C$.
Picard démontre dans son "Mémoire sur la théorie des fonctions algébriques de deux variables", (1889) J. Math. Pures et Appliquées, que le premier nombre de Betti des hypersurfaces lisses de $\mathbb P^3(\mathbb C)$ est nul. À l’opposé de la dimension $1$, on n’obtient donc qu’une classe assez restreinte de topologie de surfaces algébriques par cette construction. Par exemple, aucun tore n’apparaît ainsi, ni aucune variété hyperbolique complexe, etc.. Quelque temps plus tard, dans le IIIème complément, Poincaré complète le résultat de Picard et montre la propriété analogue pour les revêtements ramifiés double du plan projectif complexe. Mais il va plus loin, il annonce même qu’ils sont simplement connexes !
Le revêtement double de $\mathbb P^2(\mathbb C)$ ramifié le long d’une courbe lisse de degré pair est simplement connexe.
Notez que les nombres de Betti des revêtements doubles se déduisent alors aisément du théorème. En effet, on a bien sûr $b_0=b_4= 1$. D’après le théorème, on a $b_1= 0$, et par dualité (voir Dualité de Poincaré (énoncé du théorème)) $b_3=0$ également. Pour mettre la main sur le deuxième nombre de Betti, calculons la caractéristique d’Euler-Poincaré de $X$. Elle s’exprime par $\chi (X) = 2 \chi (\mathbb P^2 (\mathbb C)) - \chi (C)$ (cette formule généralise au cas ramifié celle qui donne la caractéristique d’Euler-Poincaré d’un revêtement). On a $\chi (\mathbb P^2 (\mathbb C) ) = 3$. La formule qui relie le genre au degré donne $\chi (C) = d(d-3)$. On a donc $\chi(X)=6-d(d-3)$. Comme $\chi(X)$ est par ailleurs égal à la somme alternée des nombres de Betti de $X$ (voir ici), on obtient
$$ b_2(X) = d^2 - 3d + 4.$$
La topologie des revêtements ramifiés doubles du plan projectif complexe devient donc très riche lorsque $d$ devient grand, même si elles sont simplement connexes. Pour $d=2$, on obtient des surfaces rationnelles, pour $d= 4$ des fibrations elliptiques, pour $d= 6$ les belles surfaces K3, et pour $d$ supérieur des surfaces de type général.
Qu’est ce qu’une surface K3 ?
Il s’agit d’une surface complexe compacte qui est simplement connexe, et qui admet une forme volume holomorphe qui ne s’annule en aucun point.
Le fait qu’une telle forme existe sur l’espace total d’un revêtement double du plan projectif $r: X \rightarrow \mathbb P^2(\mathbb C)$ ramifié le long d’une courbe lisse de degré $6$ vient du fait que le fibré canonique $K_X := \wedge ^2 T^* X$ s’exprime sous la forme
$$K_X = O(C') \otimes r^* K_{\mathbb P^2(\mathbb C)}$$
où $C'$ est la pré-image de $C$ dans $X$ et $r$ est le revêtement double. On montre facilement que
$$r^* O(C) = O(C')^{\otimes 2}.$$
Comme $K_{\mathbb P^2(\mathbb C)}= O(-3)$, et $O(C)= O(d)$, le fibré $K_X^{\otimes 2} $ est holomorphiquement trivial si $d= 6$. Il admet donc une section qui ne s’annule pas. Comme $X$ est simplement connexe, on peut en prendre une racine carrée, et construire de la sorte une forme holomorphe partout non nulle sur $X$.
Le deuxième nombre de Betti de ces surfaces est égal à 22.
Pour les variétés lisses simplement connexes de dimension quatre, on sait maintenant que la forme d’intersection sur le second groupe d’homologie détermine complètement la topologie de la variété (théorème de Freedman), mais c’est une autre histoire, qui lui a d’ailleurs valu son auteur la médaille fields. Nous renvoyons à Topologie des courbes algébriques réelles pour une illustration intéressante de l’utilisation de la forme d’intersection sur le $H_2$.
L’argument de Poincaré consiste à étudier les cycles évanescents de certains pinceaux sur ces surfaces, mais il comporte malheureusement une erreur (Voir nos Commentaire au troisième complément). Nous présentons ici une démonstration alternative tout en essayant de rester au plus proche de la méthode de Poincaré. Une autre démonstration, plus moderne, nous a été communiquée par Claire Voisin et démontre en fait beaucoup plus : si $Y\rightarrow X$ est un revêtement ramifié double qui ramifie le long d’une courbe $F\subset X$, et si $F$ est une fibre d’une fibration de Lefschetz de $X$, alors la simple connexité de $X$ entraine celle de $Y$. Cette démonstration est expliquée dans la vidéo
Le lecteur intéressé pourra aussi lire Topologie des hypersurfaces de l’espace projectif, dans lequel est démontré que les hypersurfaces de $\mathbb P^n (\mathbb C)$ sont simplement connexes dés que $n\geq 3$. Le point de vue est très moderne, et repose sur la théorie de Morse réelle, plutôt que sur l’utilisation d’un pinceau de Lefschetz.
Démonstration du théorème
Notre stratégie consiste à remarquer que, comme pour le cas des courbes hyperelliptiques, la topologie du revêtement ramifié ne dépend que du degré de la courbe de ramification. Cela est dû au fait que deux courbes algébriques lisses de même degré sont isotopes. En effet, une courbe algébrique étant définie par son équation homogène modulo multiplication par une constante, l’espace des courbes algébriques de degré $d$ est un espace projectif complexe de dimension $n= d (d+3)/2$. L’ensemble des courbes algébriques lisses est l’extérieur d’une sous-variété projective complexe de $\mathbb P^n (\mathbb C)$ de codimension complexe $\geq 1$. Il est donc connexe ! On notera que ce fait n’est plus du tout vrai dans le réel, car une hypersurface peut séparer un espace en plusieurs composantes : les parties réelles des revêtements doubles du plan ramifiés le long d’une courbe de degré fixé ont d’ailleurs des topologies très variées, comme nous le verrons dans l’article Topologie des courbes algébriques planes réelles.
Cela requiert la théorie de l’élimination, et est donc loin d’être évident pour un non algébriste ! Cette théorie permet d’établir que l’image d’une variété algébrique par un morphisme est une sous-variété algébrique également. Admettons cet énoncé fondamental et montrons que l’ensemble $S_d\subset \mathbb P^n(\mathbb C)$ formé par les courbes algébriques singulières est une sous-variété algébrique complexe stricte de $\mathbb P^n(\mathbb C)$. L’argument consiste à introduire le sous-ensemble $S\subset \mathbb P^n (\mathbb C) \times \mathbb P^2(\mathbb C)$ formé par les couples $([P], [p])$, où $P$ est un polynôme homogène de degré $d$ non identiquement nul sur $\mathbb C^3$, et où $p\in \mathbb C^3 \setminus 0$ est un point critique de $P$, i.e.
$$ \frac{\partial P}{\partial x}(p) = \frac{\partial P}{\partial y}(p)=\frac{\partial P}{\partial z}(p) =0.$$
L’ensemble $S$ est une sous-variété algébrique de $\mathbb P^n( \mathbb C) \times \mathbb P^2(\mathbb C)$. Sa projection dans le premier facteur $\mathbb P^n (\mathbb C)$ l’est également, par élimination. Or cette dernière est précisément $S_d$. Il reste à voir que $S_d$ n’est pas tout $\mathbb P^n (\mathbb C)$. Mais la courbe de Fermat $x^d + y^d = z^d$ est lisse, comme le lecteur peut le vérifier.
C.Q.F.D.
Il nous suffit donc de construire, pour tout $d>0$ pair, un exemple de revêtement double de $\mathbb P^2(\mathbb C)$ ramifié le long d’une courbe lisse de degré $d$ qui est simplement connexe. La construction repose sur le résultat technique suivant :
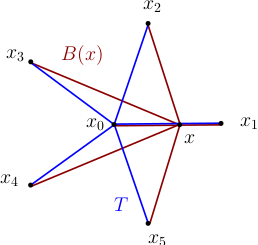
Pour tout entier $d$, il existe un polynôme $P(x,y)$ de degré $d$ en deux variables complexes, un bouquet $T\subset \mathbb C$ constitué de $d-1$ intervalles
$$T= \bigcup_{k=1}^{d-1} [x_0,x_k],$$
et $d$ applications continues $y_0, \ldots, y_{d-1} : T \rightarrow \mathbb C$ telles que :
1) la compactification de la courbe $P=0$ dans $\mathbb P^2(\mathbb C) $ est lisse, et elle admet des tangences simples avec le pinceau qui dans la carte affine $(x,y)$ est constitué des droites verticales,
2) pour tout $k=0,\ldots, d-1$, et pour tout $x \in T$, on a
$$P (x, y_k(x))= 0,$$
3) pour tout $x\in T \setminus \{ x_1,\ldots, x_{d-1} \}$, les valeurs $y_k(x)$ sont deux à deux distinctes,
4) pour tout $1\leq l,k\leq d-1$, $l \neq k$, et tout $x\in T$, $y_l(x)$ n’appartient pas au segment $[y_0(x), y_k (x)]$,
5) pour tout $k= 1,\ldots , d-1$, on a $y_0(x_k) = y_k (x_k)$.
Les propriétés (4) et (5) se reformulent en disant que pour $x\in T$, le bouquet d’intervalles $B(x)= \bigcup_{k=1}^{d-1} [y_0(x), y_k(x)]$ ne dégénère qu’aux extrémités $x=x_k$ de $T$ ; en ces dernières, l’intervalle $[y_0(x), y_k(x)]$ est contracté sur un point, le reste du bouquet étant non dégénéré.
$$ P (x,y) = (y- x ) \prod_{k= 1}^{d-1} (y - x_k ) ,$$
et on définit
$$T= \bigcup_{k= 1}^{d-1} [x_0, x_k],$$
et
$$ y_0 (x) = x , \ \ y_k (x) = x_k \text{ si } k= 1,\ldots, d-1.$$
En dehors de la première, il est aisé de vérifier toutes les propriétés du lemme.
Considérons alors une perturbation $P'$ de $P$ telle que la compactification de la courbe $P' = 0$ dans $\mathbb P^2$ est lisse. On peut faire en sorte que l’on ait $P'(x_0, x_0)= P(x_0,x_0)= 0$, ce qui va alléger les notations dans ce qui suit.
Le discriminant du polynôme $y \mapsto P(x,y)$ est égal à
$$ \delta_P (x) = \prod_{k\geq 1} ( x - x_k )^2 \prod_{1\leq k < l } (x_k - x_l)^2, $$
et comme fonction de $x$, il s’annule à l’ordre deux en chaque point $x_k$, pour $k\geq 1$. Le polynôme $P'$ étant choisit proche de $P$, le discriminant $\delta_{P'} (x)$ de $y\mapsto P'(x,y)$ est proche de $\delta_P$, et admet par conséquent deux racines $ x_k'$ et $x_k''$ proches de $x_k$. Nous choisissons la racine $x_k'$ en sorte que le segment reliant $x_0 $ et $x_k'$ ne contienne pas $x_k ''$ dans son intérieur.
Posons $T' = \bigcup_ {k= 1}^{d-1} [x_0 '= x_0, x_k ']$. Le discriminant $\delta_{ P' }(x)$ est non nul en tout point $x\in T'$ différent des extrémités $x_1',\ldots, x_{d-1} '$ de $T'$. Par simple connexité de $T' \setminus \{ x_k' \}_{k\geq 1 }$, on peut trouver de façon unique des applications continues $y' _k : T' \setminus \{ x_k' \}_{k\geq 1 } \rightarrow \mathbb C $ vérifiant
$$ P' (x , y_k'(x) ) = 0 $$
pour tout $x\in T'$, et de plus
$$ y_k '( x_0 ' ) = x_0 .$$
L’unicité et la propriété (3) découlent de ce que le discriminant de $P'$ ne s’annule en aucun point de $T'$ différent de ses extrémités.
Les applications $y_k'$ s’étendent par continuité aux extrémités de $T'$, car l’ensemble des racines d’un polynôme dépend continûment du polynôme.
La propriété (4) découle du fait que $P'$ est proche de $P$. Pour démontrer la propriété (5), il suffit de remarquer que $y_l'(x_k')$ est proche de $y_l( x_k)$ pour tout $k,l$. À $k$ fixé, on sait que parmi les $y_l'(x_k')$, il y en a deux qui coïncident car le discriminant $\delta_{P'}(x_k')$ s’annule. Ces deux valeurs doivent donc être $y_0' (x_k')= y_k'(x_k')$.
C.Q.F.D.
Soit $d>0$ un entier pair, et $P$ le polynôme construit au lemme précédent. Notons $C$ l’adhérence de $\{P=0\}$ dans $\mathbb P^2 (\mathbb C)$. Le revêtement double de $\mathbb P^2(\mathbb C)$ ramifié le long de $C$ est simplement connexe.
C.Q.F.D.
La préimage $r^{-1} (\mathcal P)$ est un pinceau qui admet deux points bases $b_1$ et $b_2$, et un nombre fini de fibres singulères $F_1,\ldots , F_s$. Notons $X' = X \setminus \big( \{ b_1,b_2\}\cup F_1 \cup \ldots \cup F_s \big)$.
La restriction de $r^{-1} (\mathbb P)$ à $X '$ est une fibration dont les fibres sont des surfaces fermées orientées de genre $k-1$ avec deux points ôtés, et la base est difféomorphe à $\mathbb P^1(\mathbb C) \setminus \{ z_1,\ldots, z_s\}$.
Soit $p_0\in F_ 0 \cap X'$ un point base, et $z_0$ son image dans $\mathbb P^1(\mathbb C) \setminus \{ z_1,\ldots, z_s\}$. Le groupe fondamental de $\mathbb P^1(\mathbb C) \setminus \{ z_1,\ldots, z_s\}$ est engendré par des courbes $\gamma_1, \ldots , \gamma_s$ faisant le tour des points $z_1, \ldots, z_s$. On peut relever ces courbes $\gamma_i$ en des courbes $\tilde{\gamma_i}$ basées en $p_0$, et qui sont homotopes à un point dans $X$ (on choisit le relevé $\tilde{\gamma_i}$ de sorte qu’il fasse le tour d’un point non singulier de $F_i$).
Prenons maintenant un élément $x\in \pi_1(X, p_0)$. On peut le représenter par une courbe $\nu$ basée en $p_0$ dont l’image est contenue dans $X'$. La projection de $\nu$ dans $\mathbb P^1(\mathbb C) \setminus \{ z_1,\ldots, z_s\}$ est homotope à un mot en les $\gamma_i$. Du coup, il existe un mot $\omega= \omega (\tilde{\gamma_1}, \ldots, \tilde{\gamma_s})$ qui est tel que la projection de la concaténation $\nu * \omega $ est homotope à $z_0$ dans $\mathbb P^1(\mathbb C) \setminus \{ z_1,\ldots, z_s \}$. Comme $r^{-1} (\mathcal P)$ est une fibration dans $X'$, on peut donc homotoper $\nu * \omega$ à un lacet dans $F_0 \cap X'$. Comme $\omega$ est trivial dans $\pi_1(X ,p_0)$, ceci signifie bien que $x= [\nu]$ est dans l’image de $\pi_1(F_0, p_0)$.
C.Q.F.D.
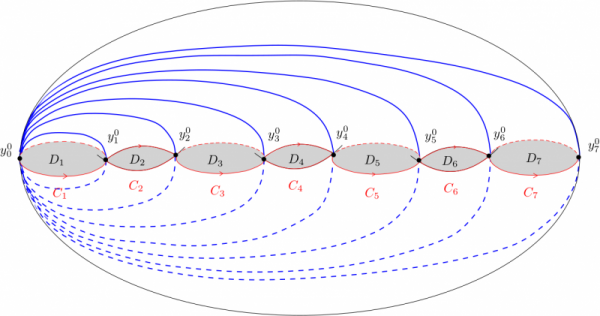
Pour $k=1,\ldots, d-1$, soit $c_k \subset F_0$ la courbe fermée simple définie par
$$c_k := r^{-1} ([x_0, x_k]).$$
Les propriétés (4) et (5) montrent que ce cycle est homotope à un point dans $X$. En effet, une homotopie explicite est définie par la famille $\{ c_k ^x \}_{x\in [x_0, x_k]}$, où $c_k^x:= r^{-1} ([y_0 (x), y_k (x)])$. La propriété (4) montre que $c_k^x$ varie continument avec $x$, et (5) montre que $c_k^{x_k}$ est constante.
Nous allons montrer que les cycles évanescents (voir bloc Groupe fondamental des fibrations de Lefschetz pour cette terminologie) $c_k$ engendrent $ \pi_1(F_0)$ en tant que sous-groupe normal, ce qui démontrera la proposition. Pour cela, représentons $F$ et les courbes $c_k$ comme sur la figure, et introduisons les courbes fermées simples $C_k$, pour $k= 1,\ldots, d-1$. On paramètre les courbes $c_k$ par $[0,1]$ de façon à ce qu’elles commencent au point $y_0^0$ puis entrent dans la partie supérieure de $F_0$. On constate que l’on a les relations
$$ C_1 \sim c_1,\ \ C_ 2 \sim c_2 * c_1^{-1}, \ldots, \ \ C_{d-1} \sim c_{d-1} * c_{d-2}^{-1},$$
où $\sim$ désigne la relation d’homotopie entre courbes fermées. En particulier, le sous-groupe normal $N$ engendré par les $c_k$ est le même que celui engendré par les $C_k$. Par la formule de Van Kampen (voir bloc Le(s) théorème(s) de Van Kampen), le quotient de $\pi_1(F_0)$ par $N$ est isomorphe au groupe fondamental de l’espace obtenu en collant à $F_0$ les disques $D_k$ représentés sur la figure. Or l’union $D= \bigcup_{k=0}^{d-1} D_k$ est simplement connexe, et pour obtenir $F\cup D$, on recolle à $D$ deux disques : les parties supérieures et inférieures de $F$. De nouveau, la formule de Van Kampen nous dit que le groupe fondamental de $F_0\cup D$ est trivial. Nous avons bien montré que les $c_k$ engendrent $\pi_1(F_0)$ en tant que sous-groupe normal.
C.Q.F.D.