
|
> Surfaces complexes > Éclatements Éclatements |
Considérons une surface $X$, pour l’instant réelle — mais plus tard complexe — et donnons nous un point $p_0$ dans $X$. L’éclatement de $X$ en $p_0$ est une surface qui est obtenue en remplaçant le point $p_0$ par l’ensemble des "directions projectives" partant de $p_0$, c’est à dire par le projectivisé du fibré tangent de $X$ en $p_0$. Le but de ce bloc est de détailler cette construction.
Supposons par exemple que $X$ est le plan réel $\mathbb R^2$, le point $p_0$ est l’origine $(0,0)$, et considérons les coordonnées polaires $(r, \theta)$. Ces derniéres définissent un difféomorphisme de $X\setminus \{ p_0 \}$ sur le cylindre $(0, \infty) \times \mathbb S^1$, qui ne se prolongent pas continûment en $p_0$ ; il y a une ambiguité pour définir la valeur de la coordonnée angulaire $\theta$ en l’origine. On prendra la convention ici que $\mathbb S^1$ est le cercle unité, que l’on identifie à $\mathbb R / 2\pi \mathbb Z$ via l’application $\theta \in \mathbb R /2\pi \mathbb Z \mapsto (\cos \theta, \sin \theta) \in \mathbb S^1$.
Pour lever cette indétermination, il suffit de chercher à inverser les coordonnées polaires, c’est à dire de considérer l’application $(r, \theta)\mapsto (r\cos \theta, r \sin \theta) $, qui est bien définie sur $[0, \infty) \times \mathbb S^1$ et à valeurs dans $\mathbb R^2$. Cette dernière induit un difféomorphisme de $(0, \infty) \times \mathbb S^1$ dans le plan privé de l’origine, mais elle "écrase" le cercle $0 \times \mathbb S^1$ sur $p_0$. Il est bien naturel de penser aux points de $0 \times \mathbb S^1$ comme des directions partant de l’origine, le point $0 \times \theta$ étant associé à la direction $\mathbb R^{>0} \theta$. On peut donc penser au cylindre $[0,\infty) \times \mathbb S^1$ comme au plan, mais où l’on a remplacé l’origine par l’ensemble des directions orientées partant de l’origine.
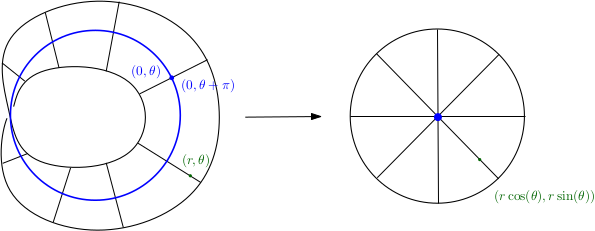
On a dit qu’on voulait remplacer le point $p_0$ par l’ensemble des directions projectives (c’est à dire non orientées !) partant du point $p_0$. On est en général pas très content de perdre de l’information, et notamment des orientations. Mais dans notre cas, nous allons voir que c’est très utile pour au moins deux raisons : d’abord nous obtiendrons un objet sans bord, et ensuite la construction se généralise bien au cas complexe.
Pour ce faire, il suffit de considérer le quotient du cylindre $[0, \infty) \times \mathbb S^1$ par l’identification $ (0, \theta) \sim (0, \theta+ \pi)$. On obtient alors une variété lisse difféomorphe à la bande de Moebius, représentée sur la figure. On note $\hat{\mathbb R^2}$ cette variété, et $\pi : \hat{\mathbb R^2} \rightarrow \mathbb R^2$ la projection naturelle, définie en coordonnée par
$$ \pi :(r,\theta) \mapsto (x=r\cos\theta, y= r\sin \theta). $$
Cette derniére induit un difféomorphisme entre $\pi^{-1} (\mathbb R^2 \setminus \{ (0,0)\})$ et $\mathbb R^2 \setminus \{ (0,0\}$. L’ouvert $\pi^{-1} (\mathbb R^2 \setminus \{ (0,0)\})$ est le ruban de Moebius privé de son âme.
Si $\phi : (\mathbb R^2 , (0,0) ) \rightarrow (\mathbb R^2, (0,0)) $ est un germe de difféomorphisme de classe $C^\infty$, alors il existe un unique germe de difféomorphisme $\hat{\phi} : (\hat{\mathbb R^2 }, \pi^{-1}((0,0))) \rightarrow (\hat{\mathbb R^2 }, \pi^{-1}((0,0))) $ tel que $\pi\circ \hat{\phi} = \phi \circ \pi$. (le lecteur aura deviné que $\hat{\phi}$ agit via la dérivée de $\phi$ sur les directions en $T_ {(0,0)} \mathbb R^2$.)
Dans le cas d’une surface réelle en général, on considère un voisinage de $p_0$ difféomorphe à $\mathbb R^2$, de sorte que le point $p_0$ soit associé à l’origine. L’éclatement de $X$ en $p_0$ est la surface $\hat{X}$ construite en remplaçant le voisinage de $p_0$ par l’éclatement de $\mathbb R^2$ construit plus haut. Plus formellement, on ôte à $X$ le disque unité $D^2\subset \mathbb R^2$ défini par $D^2 = \{ (x,y) \in \mathbb R^2 \ |\ x^2 + y^2 <1 \}$, et on lui recolle la surface $\pi^{-1} (\overline{D^2})$ via l’identification de $\pi^{-1} (\partial D^2)$ à $\partial D^2$ donnée par $\pi$.
On note $\pi _X : \hat{X} \rightarrow X$ l’application d’éclatement, qui dans la surface $ \pi^{-1} (D^2)$ est l’application $\pi$, et sur l’extérieur $X\setminus D^2$ est définie par l’"identité". La surface $\hat{X}$ et l’application d’éclatement $\pi_X :\hat{X}\rightarrow X$ ne dépend pas de la carte choisie au point $p_0$ (cela découle de l’exercice). L’éclatement d’une surface en un point est difféomorphe à la surface obtenue en ôtant un disque à $X$, et en recollant un ruban de Moebius ; il est donc difféomorphe à la somme connexe de $X$ avec le plan projectif réel $\mathbb P^2(\mathbb R)$. Nous renvoyons à Somme connexe, surface de genre $g$.
L’application $(\pi _X)_ * : \pi_1 (\hat{X} ) \rightarrow \pi_1(X)$ est surjective mais pas injective ; la classe de conjugaison induite par la courbe $\pi_X ^{-1} (p_0)$ dans $\pi_1(\hat{X})$ est dans le noyau de $p$, mais est non triviale (c’est une courbe fermée simple dont un voisinage est un anneau de Moebius donc elle s’envoit sur $-1$ par le morphisme d’orientation $\pi _1 (\hat{X} ) \rightarrow \{ \pm 1 \}$).
Voici une alternative pour définir l’éclatement. Elle permet notamment de généraliser la construction au cas complexe, et en fait, à n’importe quel corps. Dans la suite, $k$ désigne le corps $\mathbb R$ ou $\mathbb C$.
Commençons par un exemple. Considérons la fonction méromorphe $f: k^2\dashrightarrow \mathbb P^1(k)$ définie par $f (x,y) = y/x$, qui associe au point $(x,y)$ la pente de la droite qui relie l’origine au point $(x,y)$ (Voir Pinceaux et fibrations de Lefschetz pour la notion de fonction méromorphe). On regarde cette fonction comme une fonction à valeurs dans $\mathbb P^1 (k)$, son domaine de définition étant $k^2 \setminus \{(0,0)\}$. En l’origine, $f$ n’est pas bien définie, on dit qu’elle a un point d’indétermination. L’adhérence du graphe de $f$ dans $k^2 \times\mathbb P^1(k)$ est une surface quadratique, d’équation $y= z x$, si $z$ est une coordonnée affine de $\mathbb P^1(k)$. Nous notons cette surface $\hat{k^2}$ ; elle est constituée du graphe de $f$ lui-même, ainsi que de toute la droite verticale $(0,0)\times \mathbb P^1(k)$, ce qui peut se comprendre en imaginant que $f$ associe à l’origine toutes les valeurs possibles de $\mathbb P^1 (k)$. De façon inverse, notons $\pi $ l’application de l’adhérence du graphe de $f$ dans $k^2$, définie par $\pi (x,y,z) = (x,y)$. La pré-image de $(0,0)$ est une copie de $\mathbb P^1(k)$, tandis que $\pi$ induit une isomorphisme entre $\pi^{-1} (k^2 \setminus \{ (0,0)\})$ dans $k^2 \setminus \{ (0,0)\}$. Dans le cas réel ($k=\mathbb R)$, cette surface est difféomorphe à l’éclatement de $\mathbb R^2$ en l’origine que nous avons construit plus haut : un difféomorphisme explicite est donné par
$$(r,\theta)\mapsto (x=r\cos \theta, y=r\sin \theta, z=\tan \theta).$$
Supposons maintenant que $k= \mathbb C$, et prenons une surface complexe $X$ et un point $p_0$ de $X$. Il existe un voisinage de $p_0$ qui est biholomorphe à la boule $B= \{ (x,y) \in \mathbb C^2 \ |\ |x|^2 + |y|^2 <1 \}$. Comme dans le cas réel, ôtons de $X$ la boule $B$ et recollons à $X\setminus B$ la variété complexe $\pi^{-1} (B)\subset \hat{\mathbb C^2}$ via l’application $\pi$. On obtient une surface complexe que l’on note $\hat{X}$, ainsi qu’une application $\pi_X : \hat{X} \rightarrow X$ qui est définie par $\pi$ sur $\pi^{-1} (B)$ et par l’"identité" sur $X\setminus B$. Le lecteur pourra vérifier que cette surface complexe ne dépend pas de la carte choisie en $p_0 $ comme dans le cas réel.
Si $X$ est une surface complexe, $p_0\in X$, et $\pi_X : \hat{X}\rightarrow X$ est l’éclatement de $X$ en $p_0$, alors $\pi_X$ induit un isomorphisme $(\pi_X)_*$ entre $\pi_1(\hat{X})$ et $\pi_1(X)$.
Prenons maintenant une courbe fermée $\hat{c}: \partial D^2 \rightarrow \hat{X}$ dont la projection $c = \pi_X \circ \hat{c}$ est homotope à un point. Puisque $\pi_X^{-1} (p_0)$ est de codimension réelle $\geq 2$, on peut homotoper $\hat{c}$ à une courbe qui n’intersecte pas $\pi_X^{-1}(p_0)$. La courbe $c: \partial D^2 \rightarrow X\setminus \{p_0\}$ se prolonge en une application $c: D^2 \rightarrow X$. On peut homotoper cette dernière en une application dont l’image ne contient pas $p_0$ (car la somme des dimensions de $D^2$ et de $p_0$ est strictement inférieure à celle de $X$). On relève alors cette application en une application $\tilde{c}: \mathbb D \rightarrow \hat{X}$ qui prolonge $\hat{c}$. L’application $(\pi_X)_*$ est donc également injective.
C.Q.F.D.
Ce résultat dit que le groupe fondamental est un invariant birationnel des surfaces. En effet, on peut passer d’une surface complexe à une surface complexe qui lui est birationnelle par une suite d’éclatements et d’inverse d’éclatements, mais cela dépasse le cadre de ce bloc. Nous renvoyons à l’introduction Surfaces complexes pour la notion d’équivalence birationnelle.
En fait, la topologie de $\hat{X}$ est trés simple à calculer :
Si $X$ est une surface complexe et $p_0\in X$, l’éclatement $\hat{X}$ de $X$ en $p_0$ est difféomorphe (par un difféomorphisme qui préserve l’orientation) à la somme connexe de $X$ avec le plan projectif complexe munie de l’orientation opposée.
$$ (x, y ) \mapsto \big( \frac{x}{|x|^2 + |y|^2 } , \frac{y}{|x|^2 + |y|^2 } \big) $$
Cette application de $\mathbb B \setminus \{(0,0 \}$ dans $\mathbb C^2 \setminus \overline{\mathbb B} $ se prolonge en un difféomorphisme de $\hat{\mathbb B}$ dans $\mathbb P^2 (\mathbb C) \setminus \overline{\mathbb B}$. On laisse la vérification de ce fait au lecteur.
C.Q.F.D.
L’application $\pi_X $ induit un isomorphisme $(\pi_X)_*$ entre $H_i(\hat{X}, \mathbb Z)$ et $H_i(X, \mathbb Z)$ pour $i\neq 2$, et pour $i= 2$ on a une suite exacte
$$ 0\rightarrow \mathbb Z [\pi_X^{-1}(p_0)] \rightarrow H_2(\hat{X}, \mathbb Z)\stackrel {(\pi_X)_*}{\rightarrow} H_2(X, \mathbb Z)\rightarrow 0.$$
Terminons ce bloc en remarquant que si la surface $X$ est une surface algébrique munie d’un pinceau de Lefschetz défini par une fonction méromorphe $f: X\dashrightarrow \mathbb P^1(k)$ (voir bloc Pinceaux et fibrations de Lefschetz), alors l’éclatement de $X$ aux points d’indétermination de $f$ fournit une surface $\hat{X}$ sur laquelle le pinceau devient une fibration de Lefschetz. De plus, un modéle pour $\hat{X}$ est tout simplement l’adhérence dans $X\times \mathbb P^1(k)$ du graphe de $f: X \setminus \text{Ind} (f) \rightarrow \mathbb P^1(k)$ (ici $\text{Ind}(f)$ désigne l’ensemble des points d’indétermination de $f$).

