Topologie des courbes algébriques planes réelles

À l’époque où Poincaré écrit l’Analysis Situs, l’étude topologique des courbes algébriques planes réelles se développe outre Rhin, avec les travaux de Harnack, Klein, et puis Hilbert. Si Poincaré ne semble pas avoir considéré ce problème (du moins dans ses écrits), il nous a quand même semblé opportun de parler de cette théorie, qui se situe en plein cœur de l’Analysis Situs. Nous décrivons quelques morceaux choisis, et nous arrêtons avec les travaux d’Arnold du début des années 70, qui établissent un lien très intéressant avec la topologie des revêtements ramifiés doubles du plan projectif complexe.

Le problème, qui sera popularisé par Hilbert à l’occasion du congrès international de mathématiques qui se tient à la Sorbonne en août 1900 (première partie du XVIème problème), est de comprendre la disposition que peuvent prendre les ovales d’une courbe algébrique réelle plane. Un ovale est par définition une composante connexe bilatère de la courbe. Toute configuration est possible en fait, si l’on s’autorise un degré arbitraire. Par contre, comprendre la disposition des ovales d’une courbe de degré $d$ donné est une tâche bien plus ardue. Ce problème n’est actuellement complètement résolu que pour $d\leq 7$.

Topologie des courbes dans le plan projectif réel.

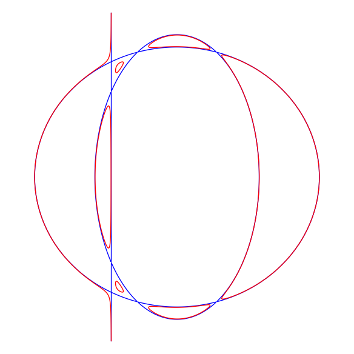
Nous dirons qu’une courbe fermée simple du plan projectif réel est bilatère si elle sépare un de ses voisinages tubulaires en deux composantes connexes, et qu’elle est unilatère sinon. Par exemple, une droite projective est unilatère, alors qu’une conique lisse est bilatère.

La disposition des ovales pour les courbes de degré $\leq 4$.

Décrivons quelques exemples. Dans le cas où $d= 1$, on a affaire à une droite projective, qui est unilatère. On sait bien qu’une conique lisse n’est constituée que d’un ovale bilatère. Les travaux de Descartes et Newton convenablement réinterprétés de manière moderne permettent de décrire les différentes configurations possibles des ovales en degrés $d= 3$ et $d= 4$.

Dans le cas $d= 3$, il n’existe au plus qu’un ovale (i.e. une composante connexe bilatère). En effet, supposons par contradiction qu’il en existe au moins deux. Chacun intersecte une droite générique en un nombre pair de point. Alors une droite (générique) reliant ces deux ovales intersectera la courbe en au moins quatre points, ce qui est contraire au fait qu’un polynôme de degré $d$ en une variable n’a au plus que $d$ racines.

En degré quatre, on peut raisonner comme suit. Nous savons que toutes les composantes connexes sont bilatères. Je dis qu’il ne peut y en avoir plus de quatre. En effet, s’il y en avait cinq, considérons cinq points, chacun sur un ovale différent, et introduisons la conique passant par ces cinq points [1]. L’intersection de cette dernière avec notre courbe algébrique contiendrait alors au moins dix points, ce qui est contraire au théorème de Bézout (voir bloc B-A-BA de topologie en géométrie algébrique complexe). Il n’y a donc au plus que quatre ovales dans ce cas.

Ajoutons qu’il existe des courbes de degré $4$ avec quatre ovales, et que dans ce cas ils sont nécessairement isotopes à quatre cercles à l’extérieur les uns des autres. Dans le cas contraire, on pourrait tracer une droite ayant six points d’intersection avec notre courbe, ce qui est impossible, toujours par le théorème de Bézout. [2]

Le nombre d’ovales.

Quels sont les nombres possibles d’ovales des courbes algébriques réelles de degré $d$ ? Cette question a été complètement traitée par Harnack dans sa thèse, voir :

La réponse est la suivante :

L’argument d’Harnack repose sur le théorème de Bézout, comme dans le paragraphe précédent. Klein, qui était son directeur de thèse, a proposé une démonstration utilisant la complexification de la courbe.

Ainsi, une courbe de degré $5$ n’a au plus que $7$ ovales, une courbe de degré $6$ au plus $11$ etc.

Courbes maximales.

Une courbe ayant le nombre maximal $g+1$ de composantes connexes, sera appelée maximale. L’existence des courbes maximales est loin d’être triviale.

Le principe est le suivant. On part d’une courbe singulière $A$ avec des points doubles ordinaires, définie par une équation $P(x,y,z)= 0$ avec $P$ homogène de degré $d$. Puis on considère un polynôme $Q$ homogène de degré $d$ qui a la propriété de ne s’annuler en aucun point singulier de $A$. Pour $\varepsilon >0$ petit, on introduit alors la famille de courbes $A_{\varepsilon}$ définies par les équations $P + \varepsilon Q$. Le lemme de Morse nous dit qu’en tout point nodal de $A$, il existe des coordonnées $u,v$ centrées telles que $P/Q = uv$. Dans ces coordonnées, la courbe $A_{\varepsilon}$ est donc l’hyperbole d’équation $uv= -\varepsilon$. À l’extérieur du domaine de définition des coordonnées $u,v$, la courbe $A_{\varepsilon}$ est une petite perturbation de la courbe $A$ par le théorème des fonctions implicites.

Observons qu’il existe deux manières topologiquement différentes de remplacer l’union des deux axes par une hyperbole comme la figure le montre : cela dépend du signe de $Q$ aux points doubles de $A$. L’espace des polynômes homogènes de degré $d$ en trois variables est de dimension $d(d+3)/2$, qui est strictement supérieure au nombre maximum de points doubles d’une courbe algébrique de degré $d$, à savoir $d(d-1)/2$. Ceci conforte l’idée qu’on devrait pouvoir choisir la désingularisation des points nodaux de $A$, mais ce n’est pas si facile à démontrer : il s’agit d’un théorème démontré par L. Brusotti dans :

On pourra par conséquent envisager les possibilités suivantes en degré $5$ : on part de l’union de deux ellipses et d’une droite comme sur la figure précédente, et on désingularise les points doubles ordinaires de cette courbe pour obtenir une courbe maximale.

Disposition des ovales pour les courbes maximales de degré six.

Jusqu’au degré cinq, la disposition des ovales d’une courbe maximale est facile à comprendre : les ovales sont extérieurs les uns des autres. Nous avons donné la démonstration de ce fait jusqu’au degré quatre. Elle repose simplement sur le théorème de Bézout.

Solution.

Considérons une courbe maximale de degré cinq. Elle a donc six ovales, et une composante unilatère. Supposons que deux des six ovales soit l’un dans l’autre. On pourra tracer une conique qui intersecte ces deux ovales, ainsi que les quatre autres ovales. Cette conique intersecte chaque ovale en un nombre pair et non nul de points, donc la courbe en au moins douze points : mais ceci contredit le théorème de Bezout !

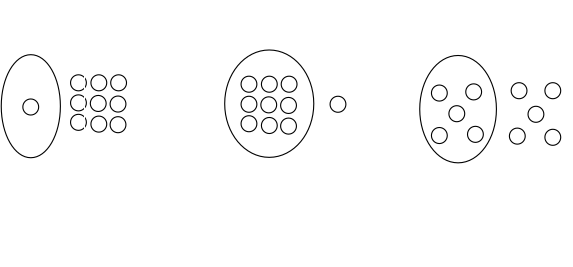
Courbes maximales en degré 6. De gauche à droite, les configurations de Harnack, Hilbert et Gudkov.

En degré six, il y a onze ovales, et la situation devient plus compliquée. Dans son article de 1891 :

Hilbert annonce pouvoir démontrer que parmi les onzes ovales d’une courbe maximale de degré six, un seul est non vide et il contient un ou neuf autres ovales, comme illustré par les deux dessins de gauche de la figure précédente. Il faudra attendre 70 années pour mettre à défaut l’énoncé de Hilbert : dans sa thèse (1967), Gudkov trouve une autre configuration, où tous les ovales sont vides sauf un seul qui contient cinq autres ovales, et il obtient la classification complète des configurations possibles pour les courbes de degré $6$.

En fait, il observe qu’une certaine congruence semble avoir lieu pour les courbes maximales de degré pair. Pour l’énoncer, considérons une courbe algébrique réelle $A$ de degré pair $d= 2k$, et choisissons un polynôme homogène $P$ définissant $A$ qui est strictement négatif sur l’unique composante connexe de $\mathbb P^2 (\mathbb R) \setminus A$ qui est non orientable. Ceci a un sens, puisque le signe d’un polynôme homogène de degré pair est bien défini dans le plan projectif réel sur chaque composante connexe du complémentaire de son lieu d’annulation. On note $\mathbb P^2(\mathbb R) ^+$ la partie de $\mathbb P^2(\mathbb R)$ où $P$ est positif. La conjecture de Gudkov, qui sera démontrée quelques années plus tard par Rokhlin, s’énonce ainsi :

Nous allons montrer ici la congruence plus faible

$$\chi (\mathbb P^2(\mathbb R) ^+ ) \equiv k^2 \pmod 4,$$

en suivant l’article novateur d’Arnol’d :

Ce type de congruence apparaît en topologie de dimension quatre : l’idée d’Arnold est de construire une variété de dimension $4$ adaptée. Naturellement, complexifier semble le meilleur moyen ; mais comment complexifier une inéquation du type $P \geq 0$ ? Arnold propose une solution qui consiste à introduire le revêtement double $r: X \rightarrow \mathbb P^2 (\mathbb C)$ ramifié le long de la complexifiée $C= A(\mathbb C)$ que nous avons étudié dans le bloc Revêtements ramifiés doubles du plan. La surface $X$ est l’hypersurface de la $3$-variété complexe

$$ E =( \mathbb C^3 \setminus 0) \times \mathbb C / (x_0, x_1, x_2, y) \sim (tx_0 , tx_1, tx_2, t^k y) $$

définie par l’équation

$$ y^2 = P (x_0, x_1, x_2) .$$

Comme notre courbe $C$ est lisse, $X$ est une surface complexe lisse. L’application de revêtement $r: X \rightarrow \mathbb P^2(\mathbb C)$ est définie par $ r (x_0,x_1,x_2, t) = (x_0, x_1,x_2) $. La conjugaison complexe sur $\mathbb P^2(\mathbb C)$ se relève à $X$ en l’involution $\sigma$ définie par

$$\sigma (x_0,x_1,x_2, t) = (\overline{x_0} , \overline{x_1}, \overline{x_2}, \overline{t}).$$

Les points fixes de cette involution, c’est à dire les points réels de $X$ que nous noterons $X(\mathbb R)$, forment une surface lisse qui est le double du domaine $\mathbb P^2(\mathbb R) ^+$. Il s’agit donc d’une surface orientable de caractéristique d’Euler-Poincaré

$$ \chi (X(\mathbb R)) = 2 \chi (\mathbb P^2(\mathbb R) ^+ ). $$

La “complexification” du domaine $\mathbb P^2(\mathbb R) ^+$ devient donc, comme l’imagine Arnold, les points réels du revêtement ramifié double le long de $C$. La congruence qu’il établit s’exprime, dans ce langage, par

$$ \chi (X (\mathbb R) ) \equiv 2 k^2 \pmod 8 .$$

Intermède arithmétique : réduction modulo deux des formes quadratiques entières.

Soit $\varphi$ une forme bilinéaire symétrique unimodulaire (c’est-à-dire de déterminant $\pm 1$) à valeurs entières sur $\mathbb Z^r$. La réduction de la forme quadratique $x\mapsto \varphi (x,x)$ modulo deux donne lieu à une forme linéaire sur le $\mathbb Z/ 2\mathbb Z$-espace vectoriel $ (\mathbb Z/ 2\mathbb Z) ^r$ ; ceci est dû à l’identité

$$ \varphi (x+y, x+y) = \varphi(x,x) + \varphi (y,y)+ 2 \varphi(x,y) \equiv \varphi(x,x) + \varphi(y,y) \pmod 2 .$$

Comme la réduction de la forme bilinéaire $\varphi$ modulo $2$ est non dégénérée (car $\varphi$ est unimodulaire), il existe un vecteur $w\in \mathbb Z^r$ telle que

$$ \varphi (x,x) \equiv \varphi (x, w) \pmod 2 $$

pour tout $x$. Un tel vecteur est appelé un élément caractéristique de $\varphi$.

Il est immédiat de voir que tous les éléments caractéristiques de $\varphi$ diffèrent par un élément pair de $\mathbb Z^r$. Si $w$ et $w'$ sont deux éléments caractéristiques, nous avons donc $w'= w+ 2x$ avec $x \in \mathbb Z^r$ et

$$ \varphi (w',w') = \varphi (w,w) + 4 (\varphi (w,x) + \varphi (x,x)). $$

Comme $\varphi (w,x)$ et $ \varphi (x,x)$ ont même parité (puisque $w$ est caractéristique), on obtient

$$ \varphi( w', w') \equiv \varphi (w,w) \pmod 8 .$$

En fait, on peut montrer en travaillant un peu plus que $\varphi(w,w)$ est congru à la signature de $\varphi$ modulo $8$. Mais nous n’aurons pas besoin de cela ici.

Démonstration de la congruence d’Arnol’d.

On note $\tau$ l’involution (dite hyperelliptique) du revêtement $r: X\rightarrow \mathbb P^2 (\mathbb C)$, définie par

$$\tau (x_0, x_1,x_2,t)= (x_0, x_1,x_2, -t),$$

et on introduit la forme bilinéaire symétrique et unimodulaire

$$ \varphi(x,y) = x\cdot \tau_* y$$

sur le module $H_2(X):= H_2( X, \mathbb Z) / \text{torsion}$ (en fait, il n’y a pas de torsion). Ici, $\cdot$ désigne la forme d’intersection.

L’ensemble des points fixes de $\tau$ est la courbe $r^{-1} (C)$ qui s’identifie naturellement à $C$ via $r$, nous la noterons $C$ dans ce qui suit.