|
> Surfaces complexes > Reconstruction topologique d’une fibration de Lefschetz Reconstruction topologique d’une fibration de Lefschetz |
Dans cet article, nous décrivons la construction d’une variété topologique $X$ de dimension 4 à partir d’une surface orientée $F$ de genre $g$ et de $n$ courbes $\gamma_1,\ldots,\gamma_n \subset F$ vérifiant une condition que l’on spécifiera. L’espace total d’une fibration de Lefschetz sera un cas particulier de cette construction : rappelons qu’il s’agit d’une surface complexe $X$ (de dimension 2 sur $\mathbb{C}$) munie d’une application holomorphe $f:X\to\mathbb{P}^1(\mathbb C)$ dont tous les points critiques sont non dégénérés, et dont les valeurs critiques correspondantes sont deux à deux distinctes. Dans ce contexte, la surface $F$ est la « fibre générique » — c’est-à-dire la préimage d’une valeur non critique fixée de $f$ — et les courbes $\gamma_1,\ldots,\gamma_n$ sont les « cycles évanescents » (voir l’article Groupe fondamental des fibrations de Lefschetz). La seconde partie de l’article est consacrée au calcul du groupe fondamental et des groupes d’homologie des variétés topologiques de dimension 4 construites auparavant. Étant donnée une surface algébrique complexe $X$, munie d’une fibration de Lefschetz, nous obtiendrons donc :
- une construction d’un modèle topologique de $X$ (faisant fi de sa structure algébrique complexe) ;
- un nouveau calcul, purement topologique, du groupe fondamental et des groupes d’homologie de $X$.
Construction topologique
On part d’une surface fermée connexe orientée $F$ de genre $g$, et de $n$ courbes fermées simples $\gamma_1,\ldots,\gamma_n$ tracées sur $F$ (on imposera plus tard une condition sur ces courbes). Pour $i=1,\ldots,n$ on se donne un voisinage tubulaire $A_i$ de la courbe $\gamma_i$, et on note $\tau_i$ un représentant du twist de Dehn à droite le long de $\gamma_i$ dont le support est inclus dans $A_i$ (c’est-à-dire tel que savoir $\tau_i(x)=x$ pour tout $x\in F\setminus A_i$). On suppose que la composée
$$\phi=\tau_n\cdots\tau_2\tau_1$$
est isotope à l’identité de $F$. On observe que $\phi$ est l’identité dans le complémentaire de la réunion des anneaux $A_i$. On peut alors choisir un point base $x_0$ dans $F$ tel que $\phi$ soit isotope à l’identité relativement à un voisinage de $x_0$.
La fibration sur la partie non-singulière
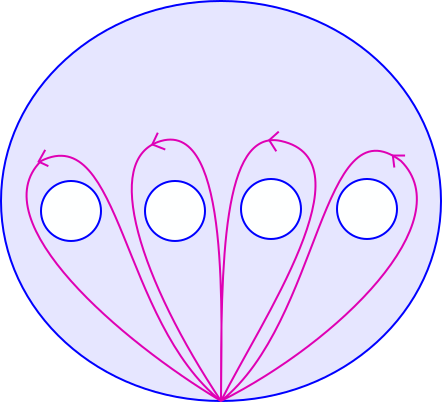
Soit $\Delta_n$ le domaine fermé de $\mathbb{C}$ égal au disque dont le diamètre est le segment $[0,n+1]$, privé de la réunion des disques de centre $i$ et de rayon $\frac 1 4$ avec $i\in\{1,\ldots,n\}$ (voir la figure ci-dessous).
Le groupe fondamental de $\Delta_n$ basé au point $y_0=(n+1)\frac{1-i}{2}$ est le groupe libre $L_{n}$ dont on a noté les générateurs $t_1,\ldots,t_n$. En particulier, le bord extérieur de $\Delta_n$ négativement orienté correspond au lacet $t_1\cdots t_n$.
On se donne une représentation $\rho:L_n\to \operatorname{Homeo}^+(F)$ en posant
$$\rho(t_i)=\tau_i.$$
Comme les chemins se composent de gauche à droite et les applications de droite à gauche, on suppose que l’on a $\rho(\alpha\beta)=\rho(\beta)\rho(\alpha)$ pour tout $\alpha,\beta\in L_n$. En particulier,
$$\rho(t_1\cdots t_n)=\tau_n\cdots\tau_1=\phi.$$
Soit $\pi:\tilde{\Delta}_n\to\Delta_n$ le revêtement universel de $\Delta_n$ basé en $y_0$. On construit une variété à bord $V$ de dimension 4 par « suspension [1] » de la représentation $\rho$ :
$$V=\left(\tilde{\Delta}_n\times F\right)/L_n$$
où $\gamma\in L_n$ agit par $\gamma.(y,x)=(\gamma.y,\rho(\gamma)(x))$. L’application $p:V\to \Delta_n$ définie par $p(x,y)=\pi(x)$ est un fibré de fibre $F$. La représentation $\rho$ est appelée monodromie du fibré $V$ et l’application $i:x\mapsto (y_0,x)$ identifie la fibre $p^{-1}(y_0)$ à $F$. On note $\tilde{x}_0$ l’image de $x_0$ par cette application : ce sera le point base de $V$.
D’après la Suite exacte de la fibration, on a la suite exacte suivante :
$$\pi_2(\Delta_n,y_0)\to\pi_1(F,x_0)\overset{i_*}{\longrightarrow} \pi_1(V,\tilde{x}_0)\overset{p_*}{\longrightarrow}\pi_1(\Delta_n,y_0)\to 1.$$
Or $\Delta_n$ est homotopiquement équivalent à un bouquet de cercles : son revêtement universel est donc contractile et $\pi_2(\Delta_n,y_0)=1$. De plus, on dispose d’une section $s$ de la suite précédente en posant $s(t_i)=[\tilde{t}_i\times x_0]$ où $\tilde{t}_i$ est un relevé de $t_i$ issu de $y_0$ dans $\tilde{\Delta}_n$.
La section $s$ nous donne donc un isomorphisme
$$\pi_1(V)=\pi_1(F,x_0)\rtimes \mathbb{L}_n$$
où le générateur $t_i$ de $\mathbb{L}_n$ agit sur $\pi_1(F,x_0)$ par $\tau_{i*}$.
Fibres singulières et chirurgie
Soit $d_i$ le bord du $i$-ème cercle intérieur de $\Delta_n$ et $M_i=p^{-1}(d_i)$. L’application $p:M_i\to d_i$ est toujours une fibration et sa monodromie est le twist de Dehn $\tau_i$. On dit que $M_i$ est le tore [2] de l’application $\tau_i$. Cette variété peut être construite plus explicitement de la manière suivante :
$$M_i=\left(F\times[0,1]\right)/\sim\text{ où }(x,1)\sim (\tau_i(x),0).$$
Observons que cette même variété s’obtient aussi par chirurgie de la façon suivante.
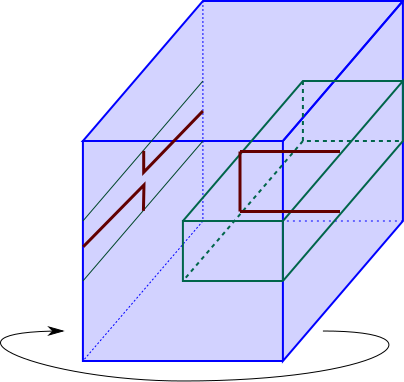
Soit $T_i=A_i \times [\frac 1 2,1]\subset M_i$. Il s’agit d’un tore plein, c’est-à-dire une variété topologique homéomorphe à $\mathbb{D}^2\times \mathbb{S}^{1}$. De plus, comme $\tau_i$ est l’identité sur $F\setminus A_i$, on a l’égalité
$$M_i\setminus T_i =\left(F\times \mathbb{S}^{1}\right)\setminus \left(A_i\times [\frac{1}{2},1]\right).$$
Dans cette formule, on a identifié $\mathbb{S}^{1}$ avec $\mathbb{R}/\mathbb{Z}$. Il s’agit bien d’une chirurgie de Dehn : en ôtant un tore plein dans $F\times \mathbb{S}^{1}$ et en le recollant différemment, on obtient $M_i$. Précisément, on recolle le tore plein $\mathbb{D}^2\times \mathbb{S}^{1}$ de la façon suivante : la courbe $\mathbb{S}^{1}\times \{1\}$ correspond au bord du carré $\alpha_i\times [\frac{1}{2},1]\subset T_i$ où $\alpha_i$ est un arc traversant l’anneau $A_i$. Son bord, vu dans $F\times \mathbb{S}^{1}$ est la courbe rouge dans la figure ci-dessous
$$\delta_i=\left(\partial\alpha_i\times [\frac 1 2,1]\right)\cup\left(\alpha_i\times\{\frac 1 2\}\right)\cup \left(\tau_i(\alpha_i)\times\{1\}\right)$$
On construit maintenant une variété $V_i$ dont le bord est $M_i$. On pose
$$V_i=\left(F\times \mathbb{D}^{2}\right)\cup_{\phi_i} \left(\mathbb{D}^{2}\times \mathbb{D}^{2}\right).$$
Dans cette formule, $\phi_i:\mathbb{S}^1 \times\mathbb{D}^{2}\to F\times \mathbb{S}^{1}$ est un plongement d’image $A_i\times [\frac 1 2, 1]$ qui envoie $\mathbb{S}^{1}\times\{1\}$ sur la courbe $\delta_i$. Par construction, le bord de la variété $V_i$ s’identifie à la variété $M_i$ vu qu’on a
$$\partial V_i=\left(F\times\mathbb{S}^{1}\right) \setminus \left(A_i\times [\frac 1 2,1]\right)\cup_{\phi_i}\left(\mathbb{D}^{2}\times\mathbb{S}^{1}\right). $$
Soit $d_0$ le cercle extérieur de $\Delta_n$, on doit traiter différemment ce cas puisque cette fois, la variété $M_0=p^{-1}(d_0)$ est le tore de l’application $\tau_n\cdots\tau_1$ qui est isotope à l’identité. Soit $\Phi:F\times[0,1]\to F$ une application continue qui vérifie que $x\mapsto \Phi(x,t)$ est un homéomorphisme pour tout $t$ qui vaut $\tau_n\cdots\tau_1$ si $t=1$ et l’identité si $t=0$. Une telle application $\Phi$ existe par hypothèse.
On pose alors
$$V_0=\left(\mathbb{D}^{2}_+\times F\right) \cup_{\psi} \left(\mathbb{D}^{2}_-\times F\right)$$
où
$$\mathbb{D}^{2}_{\pm}=\{z\in\mathbb{C}, |z|\le 1, \pm\textrm{Im}(z)\ge 0\}$$
et
$$\psi:\left(\mathbb{D}^{2}_-\cap\mathbb{R} \right)\times F\to \left(\mathbb{D}^{2}_+\cap\mathbb{R}\right)\times F$$
est définie par
$$\begin{array}{lll} \psi(t,x) & = & (t,x) & \mbox{ si } t\le 0\\ \psi(t,x) & = & (t,\Phi(x,t)) & \mbox{ si } t\ge 0. \end{array}$$
On a ainsi
$$\partial V_0=M_0.$$
On peut finalement construire $X$ par la formule
$$X=V\cup \bigcup_{i=0}^nV_i$$
de sorte que $X$ est une variété orientée compacte et sans bord de dimension 4.
Pourquoi cette variété $X$ est-elle un modèle pour une fibration de Lefschetz ?
Ce n’est pas du tout évident ! Le point crucial consiste à montrer que les fibres singulières d’une fibration de Lefschetz admettent des voisinages qui sont homéomorphes à un produit $D\times F$ auquel on a ajouté une anse d’indice deux comme indiqué précédemment. Nous allons démontrer ce fait à l’aide d’un argument de théorie de Morse.
Dans ce qui suit, nous utilisons sans rappel la description (locale et globale) des fibrations de Lefschetz faite dans les articles précédents (ici, ici et ici). On note $D= \{ (x,y)\in \mathbb R^2 \ |\ x^2 + y^2 \leq 1 \}$ le disque unité fermé de dimension $2$ orienté via l’orientation directe.
Ajout d’une anse d’indice deux. Soit $X^-$ une variété compacte à bord orientée de dimension quatre. L’ajout d’une anse d’indice deux à $X^-$ se fait via la donnée d’un plongement lisse
$$\Gamma : \partial D \times D \rightarrow \partial X^-$$
qui préserve l’orientation. L’anse $D \times D$ est recollée à $X^-$ via l’application $\Gamma$, pour obtenir une nouvelle variété de dimension quatre $X^+$ à bord et à coins. On munit $D\times D$ de l’orientation opposée à l’orientation standard de manière à obtenir une orientation bien définie sur $X^+$.
Le type topologique de la variété $X^+$ ne dépend que de la classe d’isotopie du plongement $\Gamma$. Celle-ci est déterminée par le noeud orienté $\mathcal N$ défini comme la classe d’isotopie de la courbe $ \gamma = \Gamma(\partial D \times 0)$, ainsi que par la parallélisation de ce noeud donnée par $\Gamma$. Par définition, une parallélisation est un isomorphisme du fibré normal du noeud avec le fibré trivial au dessus du cercle, qui préserve l’orientation. Etant donnée une parallélisation d’un noeud, une section parallèle est l’image d’une section constante par cette trivialisation, ou d’une trivialisation homotope. À homotopie près, une parallélisation d’un noeud est complètement déterminée par une de ses sections parallèles (exercice !).
Pour tout entier $n\in \mathbb Z$, considérons le nouveau plongement
$$\Gamma_n ( \zeta , z) = (\zeta, z \zeta^n).$$
(ici nous avons identifié $D$ avec le disque unité $\mathbb D$ via $(x,y) \mapsto x+iy$). Nous dirons que $\Gamma_n$ tourne à gauche (resp. droite) $|n|$ fois par rapport à $\Gamma$ si $n$ est positif (resp. négatif). La topologie de $X^+$ dépend à la fois du noeud et de cet entier $n$. On décrit de cette façon toutes les parallélisations d’un noeud donné. Ceci est dû au fait que le groupe $GL^+_2(\mathbb R)$ se rétracte par déformation sur son sous-groupe compact maximal $SO(2,\mathbb R)$ (exercice !).
Passage d’un point d’indice deux en théorie de Morse. Soit $m: X \rightarrow \mathbb R$ une fonction de Morse, et $[a,b]\subset m(X)$ un intervalle ne contenant qu’une seule valeur critique $c\in (a,b)$. Supposons que $c$ est d’indice deux. Rappelons que cela signifie que l’on a des coordonnées centrées au point critique associé à $c$, en lesquelles $m$ s’écrit $m(x,y,z,t) = -x^2 - y^2 + z^2 + t^2 + c$. La théorie de Morse nous dit que le sous-niveau $X^{m \leq b}$ est obtenu à partir du sous-niveau $X^{m \leq a}$ par l’ajout d’une anse d’indice deux. Cette anse est attachée au noeud de $\partial X^{m \leq a}$ défini par la courbe
$$ (x, y ) \in \partial D \mapsto \sqrt{c-a} \cdot ( x,y, 0,0) \in \partial X^{m \leq a} $$
d’image $\gamma$ muni de la parallélisation donnée par
$$ (x,y, a, b) \in \partial D \times \mathbb R^2 \mapsto ( x \sqrt{c-a} , y \sqrt{c-a} , z= b , t=a) \in N_\gamma. $$
(cette parallélisation préserve bien l’orientation, vis à vis de l’orientation naturelle de $\partial X^{m \leq a}$). Nous aurons en fait besoin d’utiliser la théorie de Morse dans le cas où $X$ a du bord. La théorie fonctionne alors de façon identique si l’on suppose que la fonction de Morse est sans point critique sur le bord.
Voisinage des fibres singulières d’une fibration de Lefschetz. On note $C \subset \mathbb C$ le carré $[-1,1]+ i [-1,1]$. Soit $ f : X \rightarrow C$ une fibration de Lefschetz, qui n’admet qu’une valeur critique, située en l’origine. La partie réelle de $f$
$$ m:= \Re f$$
est une fonction de Morse sur $X$. En effet, son unique point critique est celui de $f$, et si l’on considère des coordonnées complexes $(x_1,x_2)$ sur $X$ telles que $f(x_1,x_2) = x_1^2 + x_2^2$, donnée par le lemme de Morse holomorphe, nous avons
$$ m ( x_1, x_2 ) = u_1^2 + u_2^2 - v_1^2 - v_2^2 ,$$
avec $u_k = \Re x_k$ et $v_k = \Im x_k$. La théorie de Morse nous dit donc que si $a>0$ est suffisamment proche de $0$, $X^{m\leq a}$ s’obtient à partir de $X^{m \leq -a} $ en ajoutant une anse d’indice deux. Calculons le noeud ainsi que le parallélisme qui permet de définir cette anse. D’après ce qui précède, il s’agit de la courbe $\gamma = 0 \times \sqrt{a} \partial D^2$, paramétrée de façon directe, et le parallélisme est donné par
$$ (x,y, a, b) \in \partial D \times \mathbb R^2 \mapsto (u_1= a, u_2= b, v_1= x \sqrt{a} , v_2 =y \sqrt{a}) \in N_\gamma. $$
(le fait que l’on intervertisse pas $u_1$ et $u_2$ ici vient du fait que l’on a changé l’orientation naturelle de $X$ induite par sa structure complexe, en transposant les coordonnées $v_1$ et $u_2$). Observons que la courbe $\gamma$ est contenue dans la fibre $f^{-1} (-a)$ : il s’agit du cycle évanescent. De plus, la variété $\partial X^{m \leq -a}$ est elle-même fibrée par les niveaux de l’application $f$. On a donc un parallélisme $\Gamma$ de $\gamma$ dans $\partial X^{m \leq -a}$ dans lequel une section parallèle est envoyée sur une section tangente à $f^ {-1} (-a)$. Calculons cette section dans les coordonnées $u_k, v_k$. Comme la fibration est holomorphe, il suffit de multiplier une section du fibré tangent à $\gamma$ par le nombre complexe $i= \sqrt{-1}$. Une section du fibré tangent à $\gamma$ est donnée par le champ $v_2 \frac{\partial }{\partial v_1} - v_1 \frac{\partial}{\partial v_2}$. Comme $\frac{\partial}{\partial u_k} = \frac{\partial}{\partial v_k}$, notre section parallèle est finalement donnée par le champ $-v_2 \frac{\partial }{\partial u_1} + v_1 \frac{\partial}{\partial u_2}$. La parallélisation de $\gamma$ que l’on cherche fait donc un tour à droite par rapport à la parallélisation $\Gamma$.
Conclusion. Soit $f: X \rightarrow \Sigma$ une fibration de Lefschetz de fibre régulière $F$. Soit $F_0$ une fibre singulière de $f$, et $\gamma\subset F$ le cycle evanescent associé à $F_0$. Le paragraphe précédent montre que $F_0$ admet un voisinage qui est homéomorphe à $D\times F$ auquel on a collé une anse d’indice deux, le long du noeud $p \times \gamma \subset \partial D \times F$, qui est muni de la parallélisation qui fait un tour à droite vis à vis de la parallélisation constante de $\partial D \times F$. De plus, nous pouvons supposer que ce voisinage est une union de fibres de la fibration. En recollant ces voisinages avec le reste de la fibration, et en utilisant la formule de Picard-Lefschetz, on parvient à montrer que la variété totale $X$ est bien homéomorphe à la variété construite à partir de la donnée des cycles évanescents sur $F$.
Il existe des exemples de variétés $X$ construites comme précédemment qui ne sont pas des fibrations de Lefschetz holomorphes. Le lecteur intéressé par ces constructions pourra consulter le livre très complet sur la topologie en dimension quatre :
Robert Gompf, Andras Stipsicz. 4-manifolds and Kirby calculus. Graduate studies in mathematics. American Mathematical Society.
Calcul du groupe fondamental
Le calcul du groupe fondamental des fibrations de Lefschetz a déjà été fait, mais nous le revisitons dans le cadre plus général de la variété $X$ décrite au paragraphe précédent. Cela nous permettra de revoir le théorème de Van Kampen !
Dans la variété $X$, les sous-ensembles $V$ et $(V_i)_{i=0,\ldots,n}$ sont des sous-variétés à bord. On peut en considérer des voisinages tubulaires $U$ et $(U_i)_{i=0,\ldots_n}$ qui se rétractent par déformation sur les variétés correspondantes. De plus, pour tout $i$, l’ouvert $U\cap U_i$ se rétracte par déformation sur la variété $M_i$ qui est connexe par arcs. On peut alors calculer le groupe fondamental de $X$ à l’aide du Théorème de Van Kampen en ajoutant successivement les variétés $V_i$ et on aboutit au théorème suivant :
Soit $\gamma_i'$ un représentant de $\gamma_i$ dans $\pi_1(F,x_0)$ et $N=\langle\gamma'_1,\ldots,\gamma'_n\rangle$ le sous-groupe distingué engendré par ces lacets. On a alors l’isomorphisme
$$\pi_1(X,\tilde{x}_0)\simeq\pi_1(F,x_0)/N.$$
Démonstration. Pour tout $i\in\{0,\ldots,n\}$ on note $d'_i$ la courbe $[\tilde{d}_i\times\{x_0\}]\subset V$ où $\tilde{d}_i$ est un relevé quelconque de $d_i$ dans $\tilde{\Delta}_n$.
Appliquons le Théorème de Van Kampen aux ouverts $U$ et $U_0$. Chacun des ouverts $U,U_0$ et $U\cap U_0$ est connexe par arcs et contient le point base $\tilde{x}_0$. On a donc
$$\pi_1(U\cup U_0)\simeq\pi_1(U)\underset{\pi_1(U\cap U_0)}{*}\pi_1(U_0)\simeq\pi_1(M)\underset{\pi_1(M_0)}{*}\pi_1(W_0).$$
Or la paire $(V_0,M_0)$ est homéomorphe à la paire $(\Sigma\times\mathbb{D}^{2},\Sigma\times\mathbb{S}^1)$ et l’application $\pi_1(M_0)\to\pi_1(V_0)$ est surjective de noyau engendré par la courbe $d'_0$. On en déduit l’isomorphisme
$$\pi_1(U\cup U_0)\simeq\pi_1(V)/\langle d'_0\rangle$$
Dans cette formule, on remarque que le sous-groupe distingué engendré par certaines courbes ne dépend que de leur classe d’homotopie libre. On peut donc quotienter par des courbes qui ne sont pas issues du point base.
Ajoutons l’ouvert $U_1$, les autres ouverts se traitant de la même façon : on se donne un point base $y_1$ sur le cercle $d'_1\subset V$. En applicant le théorème de Van Kampen aux ouverts $U\cup U_0$ et $U_1$, on obtient l’isomorphisme
$$\pi_1(U\cup U_0\cup U_1)\simeq\pi_1(V\cup V_0)\underset{\pi_1(M_1)}{*}\pi_1(V_1)$$
La variété $V_1$ est elle-même réunion des variétés $\Sigma\times \mathbb{D}^2$ et $\mathbb{D}^2\times\mathbb{D}^2$. On en déduit que $\pi_1(V\cup V_0\cup V_1)$ s’obtient de $\pi_1(V\cup V_0)$ en quotientant successivement par la courbe $\delta_1$ (en ajoutant $\mathbb{D}^2\times\mathbb{D}^2$) puis la courbe $d'_1$ (en ajoutant $\Sigma\times\mathbb{D}^2$).
Mettant bout à bout tous les collages, on trouve finalement la description suivante :
$$\pi_1(X)\simeq\pi_1(V)/\langle d'_i,i=0,\ldots,n, \delta_i,i=1,\ldots,n\rangle$$
En effet, via l’isomorphisme
$$\pi_1(V,\tilde{x}_0)\simeq\pi_1(F,x_0)\rtimes L_n=\langle t_1,\ldots t_n,\gamma\in \pi_1(F)|t_i\gamma t_i^{-1}=\tau_{i*}\gamma\rangle,$$
on a $d'_i=t_i$ et $\delta_i=\gamma_i't_i$. On en déduit
$$\pi_1(X)\simeq\langle t_i,\gamma| t_i=1, \gamma_i'=1, t_i\gamma t_i^{-1}=\tau_{i*}\gamma\rangle$$
Or $\tau_{i*}$ agit trivialement sur le quotient $\pi_1(F)/\langle \gamma_i'\rangle$, ainsi la dernière relation est redondante et on a finalement
$$\pi_1(X)\simeq\langle \gamma | \gamma_i'=1\rangle=\pi_1(F ,x_0)/N.$$
C.Q.F.D.
Homologie et construction géométrique des cycles
Les nombres de Betti de la variété $X$ se calculent exactement de la même manière que dans l’article Homologie des fibrations de Lefschetz :
- $b_0(X)$ et $b_4(X)$ sont évidemment égaux à $1$ ;
- $b_1(X)$ s’obtient grâce à la description du groupe fondamental donnée ci-dessus, et au théorème d’Hurewicz ;
- $b_3(X)$ est égal à $b_1(X)$ par dualité de Poincaré ;
- la construction de la variété $X$ décrite ci-dessus, et les propriétés d’additivité, multiplicativité,... de la caractéristique d’Euler-Poincaré permettent de calculer facilement la caractéristique d’Euler-Poincaré $\chi(X)$ ;
- comme $\chi(X)$ est égale à la somme des nombres de Betti de $X$, et que l’on connait tous ces nombres sauf $b_2(X)$, c’est terminé !
Dans le Quatrième complément à l’Analysis Situs, Poincaré emprunte un chemin différent : il calcule explicitement les cycles de $X$ et les décrit géométriquement, ce qui est bien plus difficile, mais également plus instructif. Sa preuve utilise une décomposition cellulaire un peu problématique car elle dégénère sur les points singuliers. Cependant on peut rendre rigoureux ses calculs, comme c’est fait par exemple dans
Klaus Lamotke, The topology of complex projective varieties after S. Lefschetz, Topology, 20 (1981) p. 15-51.
Plus modestement, nous proposons de décrire géométriquement les cycles à la manière de Poincaré, mais sans démonstration. Bien sûr, le générateur de $H_0(X,\mathbb{R})$ est donné par la classe d’un point quelconque tandis que le générateur de $H_4(X,\mathbb{R})$ est donné par la classe fondamentale de $X$. Il reste à décrire les cycles de dimensions 1, 2 et 3.
Cycles de dimension 1
Pour chaque cycle évanescent $\gamma_i$, on note $\tilde{\gamma}_i$ un représentant de $\gamma_i$ dans la fibre $F$. Pour former une base de $H_1(X,\mathbb{R})$, il suffit de considérer une famille de courbes $\delta_1,\ldots, \delta_{2g-k}$ dans $F \subset X$ telle que la famille des classes $[\tilde{\gamma_1},\ldots,[\tilde{\gamma}_n],[\delta_1],\ldots,[\delta_{2g-k}]$ engendre $H_1(F,\mathbb{R})$. Géométriquement, le premier groupe d’homologie de $X$ est "porté" par la fibre générique.
Cycles de dimension 2
La classe fondamentale de la fibre générique $F$ et celle de la base $\mathbb{P}^1(\mathbb{C})$ [3] « comptent pour le 2 » dans la formule $b_2=2+n-2k$. De plus, elles se coupent transversalement en un point.
Choisissons une courbe fermée simple $\delta$ quelconque dans la fibre générique et faisons la tourner autour du $i$-ème trou, elle devient la courbe $\tau_{i*}\delta$ où $\tau_{i*}$ est l’action du twist de Dehn le long de $\gamma_i$ en homologie. Par construction, elle s’écrit
$$\tau_{i*}\delta=\delta+ (\delta\cdot \gamma_i) \gamma_i.$$
La surface ainsi balayée par $\delta$ est un cylindre dont le bord s’écrit $\tau_{i*}\delta-\delta$ dans l’homologie de $F$. Si $\tau_{i*}\delta=\delta$ alors ce cylindre devient un 2-cycle, mais ce cycle borde un 3-cycle obtenu en balayant $\delta$ à travers le $i$-ème trou. Ainsi, seules comptent les courbes $\delta$ qui ne sont pas fixées par $\tau_{i*}$, à savoir celles qui ne rencontrent pas trivialement $\gamma_i$. Cela fait une seule dimension par singularité, et on note $\delta_i$ une telle courbe. La condition de recollement s’écrit
$$-\delta_1+\tau_{1*}\delta_1-\tau_{1*}\delta_2+\tau_{2*}\tau_{1*}\delta_2-\tau_{2*}\tau_{1*}\delta_3+\cdots -\tau_{(n-1)*}\cdots\tau_{1*}\delta_n+\delta_n=0$$
Un calcul utilisant la formule de Picard-Lefschetz montre que cette condition fournit $k$-contraintes sur les cycles $\delta_i$, donnant $n-k$ dimensions pour le nombre de Betti $b_2(X)$.
C’était sans compter sur la contribution de $V_0$ ! Toute courbe $\delta$ que l’on fait balayer autour du disque percé des singularités crée un cylindre qui borde dans $V_0$, donc aussi dans $X$. Ainsi, il faut quotienter l’espace de cycles précédent par l’application envoyant une courbe $\xi$ sur le $n$-uplet $(\xi, \tau_{1*}^{-1}\xi, \tau_{1*}^{-1}\tau_{2*}^{-1}\xi,\ldots)$. Cela disqualifie encore un sous-espace à $k$-dimensions de l’espace de cycles précédent, et on se retrouve avec le nombre de Betti $n-2k$ que l’on cherchait à expliquer.
Cycles de dimension 3
Chaque cycle $\delta$ ne rencontrant aucun cycle évanescent peut être balayé à travers toutes les singularités, cela signifie que --- au moins au niveau homologique --- on peut fabriquer un 3-cycle comme « produit de $\delta$ par la base $\mathbb{P}^1(\mathbb{C})$ ». Le nombre de tels 3-cycles est égal à $2g-k$, et ces derniers sont bien les générateurs du groupe $H_3(X,\mathbb{R})$.
[3] Par construction de $X$, il existe une section canonique $s$ de la fibration de Lefschetz $f$. Quand nous écrivons de « la classe fondamentale de la base $\mathbb{P}^1(\mathbb{C})$ », il s’agit en fait de l’image de cette classe par $s_*$.