
|
> Homologie > L’homologie "à la Poincaré" > Comparaison entre homologie à la Poincaré et homologie singulière > Homologie à la Poincaré, homologie des simplexes plongés, homologie (...) Homologie à la Poincaré, homologie des simplexes plongés, homologie non-singulière, homologie singulière |
Dans toute la suite, on considère une variété (lisse sans bord) orientée $X$. Le but de cet article est de construire une chaîne de morphismes reliant l’homologie à la Poincaré à l’homologie singulière de $X$. Pour ce faire, on définira les groupes d’homologie singulière, d’homologie non-singulière, et d’homologie des simplexes plongés de $X$, puis des morphismes entre ces groupes.
Simplexes singuliers, non-singuliers et plongés
Dans un espace affine $E$, on appelle $p$-simplexe géométrique affine l’enveloppe convexe de n’importe quel $(p+1)$-uplet de points affinement indépendants de $E$. Pour tout $p$ et tout $i\leq p$, nous noterons $v_p^i$ le point de $\mathbb{R}^p$ dont toutes les coordonnées sont nulles, sauf la $i^{eme}$ qui estt égale à $1$. Le $p$-simplexe géométrique standard, traditionnellement noté $\Delta_p$, est l’enveloppe convexe, dans $\mathbb{R}^{p+1}$, des points $v^1_{p+1},\dots,v^{p+1}_{p+1}$. L’orientation standard de $\Delta_p$ est celle pour laquelle $\left(v_{p+1}^2-v_{p+1}^1,v_{p+1}^3-v_{p+1}^1,\dots,v_{p+1}^{p+1}-v_{p+1}^1\right)$ est une base directe.
Un $p$-simplexe singulier à valeurs dans $X$ est une application continue $\sigma:\Delta_p\to X$. Dans le cas où $\sigma:\Delta_p\to X$ est un plongement lisse [1], nous dirons que $\sigma$ est une $p$-simplexe non-singulier à valeurs dans $X$. Si $\sigma:\Delta_p\to X$ est un $p$-simplexe non-singulier, nous dirons que son image $V=\sigma(\Delta_p)\subset X$ est un $p$-simplexe plongé dans $X$, et nous dirons que $\sigma$ est un paramétrage du simplexe plongé $V$. Si $V$ est muni d’une orientation, et si cette orientation coïncide avec l’image par $\sigma$ de l’orientation standard de $\Delta_p$, alors nous dirons que $\sigma$ est un paramétrage direct de $V$.
Si $X$ est un espace affine, on pourra parler de $p$-simplexes singuliers non-singuliers affines à valeurs dans $X$ : ce sont les plongement affines de $\Delta_p$ dans $X$. Remarquons que les images des $p$-simplexes non-singuliers affines à valeurs dans $X$ sont alors exactement les $p$-simplexes géométriques affines de $X$ (on rappelle qu’un $p$-simplexe géométrique affine de $X$ est l’enveloppe convexe de $p+1$ points affinement indépendants).
Pour chaque $p\in\mathbb{N}$, nous noterons :
- $C_p^{Sing}(X)$ le $\mathbb{Z}$-module libre engendré par les $p$-simplexes singuliers à valeurs dans $X$ ;
- $C_p^{NonSing}(X)$ le sous-module de $C_p^{Sing}(X)$ engendré par les simplexes non-singuliers ;
- $C_p^{Plonges}(X)$ le $\mathbb{Z}$-module libre engendré par les $p$-simplexes plongés orientés dans $X$, quotienté par la relation qui identifie $-V$ à $V$ muni de l’orientation opposée.
Rappelons que $C_p^\square(X)$ désigne le $\mathbb{Z}$-module libre engendré par les sous-variétés polyédrales orientées de dimension $p$ de $X$, quotienté par la relation d’équivalence qui identifie $-V$ à $V$ munie de l’orientation opposée. On remarque que tout $p$-simplexe plongé dans $X$ est une sous-variété polyédrale de dimension $p$ de $X$. Ainsi $C_p^{Plongés}(X)$ s’injecte naturellement dans $C_p^\square(X)$.
Les éléments de $C_p^{Sing}(X)$, $C_p^{NonSing}(X)$, $C_p^{Plonges}(X)$ et $C_p^\square(X)$ seront appelés respectivement $p$-chaînes singulières, $p$-chaînes non-singulières, $p$-chaînes plongées et $p$-chaînes à la Poincaré.
Facettes, faces et bord
Soit $\Delta$ un $p$-simplexe géométrique affine dans un espace affine $E$. Par définition, $\Delta$ est l’enveloppe convexe de $p+1$ points affinement indépendants de $E$, que l’on appelle sommets de $\Delta$. Pour $0\leq q\leq p$, on appelle $q$-facette de $\Delta$ l’enveloppe convexe de $q+1$ de ces sommets. En particulier, les $0$-facettes de $\Delta$ sont ses sommets, et la seule $p$-facette de $\Delta$ est $\Delta$ lui-même. Les $(p-1)$-facettes sont parfois simplement appelées faces.
Considérons maintenant le cas particulier du $p$-simplexe géométrique standard $\Delta_p$. Rappelons que les sommets de $\Delta_p$ sont numérotés $v_{p+1}^1,\dots,v_{p+1}^{p+1}$. Toute $q$-facette de $\Delta_p$ est bien sûr en bijection affine avec le $q$-simplexe géométrique standard $\Delta_q$. De plus, la numérotation des sommets permet de choisir une bijection affine privilégiée. Plus précisément, si $F$ est une $q$-facette de $\Delta_p$, alors il existe $i_1 < \dots < i_{q+1}$ tels que
$$F=\mathrm{Conv}\left(v^{i_1}_{p+1},\dots,v^{i_{q+1}}_{p+1}\right).$$
On appellera paramétrage affine standard de $F$ la bijection affine $\theta_F:\Delta_q\to F$ qui envoie les points $v^{1}_{q+1},\dots,v^{q+1}_{q+1}$ sur les points $v^{i_1}_{p+1},\dots,v^{i_{q+1}}_{p+1}$ dans cet ordre.
L’image par ce paramétrage standard de l’orientation standard de $\Delta_q$ munit $F$ d’une orientation, que nous appellerons... orientation standard de $F$ !
Si $\sigma:\Delta_p\to X$ est un $p$-simplexe singulier, une $q$-facette de $\sigma$ est la composée de la restriction de $\sigma$ à une $q$-facette $F$ du simplexe géométrique standard $\Delta_p$ et du paramétrage affine standard de $F$. C’est donc un $q$-simplexe singulier à valeurs dans $X$. Dans le cas particulier où $\sigma$ est un simplexe non-singulier, ses $q$-facettes sont des $q$-simplexes non-singuliers.
Soit maintenant $V$ un $p$-simplexe plongé dans $X$. Par définition, $V$ est l’image d’un $p$-simplexe non-singulier $\sigma:\Delta_p\to X$. Une $q$-facette de $V$ est l’image d’une $q$-facette de $\sigma$, munie de l’image de l’orientation de $\Delta_q$. De manière équivalente, une $q$-facette de $V$ est l’image de la restriction de $\sigma$ à une $q$-facette de $\Delta_p$. Si $V$ est orienté, et si son orientation est l’image par $\sigma$ de l’orientation standard de $\Delta_p$, alors les $q$-facettes de $V$ seront munies des images par les $q$-facettes de $\sigma$ de l’orientation standard de $\Delta_q$. Clairement, les $q$-facettes de $V$ ne dépendent que de $V$, et pas du choix du paramétrage $\sigma$ (on utilise ici le fait que $\sigma$ est un plongement, est non pas une simple application continue). Si $V$ est orienté et si $\sigma$ est un paramétrage direct de $V$, alors on munit chaque $q$-facette de $V$ de l’image de l’orientation standard de $\Delta_q$ par la $q$-facette de $\sigma$ correspondante. On vérifie que cette orientation ne dépend que de l’orientation de $V$, et non pas du choix de $\sigma$. On appelle intérieur de $V$ l’image par $\sigma$ de l’intérieur (au sens topologique) du $p$-simplexe géométrique standard $\Delta_p$. Autrement dit, l’intérieur de $V$, c’est $V$ privé de l’union de ses faces (c’est-à-dire de ses $(p-1)$-facettes).
Nous avons remarqué ci-dessus qu’un $p$-simplexe plongé dans $X$ (orienté) est une sous-variété polyédrale de dimension $p$ de $X$ (orientée). Nous avons défini ici une notion de $q$-facette (orientée) pour les sous-variétés polyédrales. Si $V$ est un $p$-simplexe plongé dans $X$, on vérifiera facilement que les $q$-facettes (orientées) de $\Delta$ en tant que $p$-simplexe plongé (orienté) coïncident avec ses $q$-facettes (orientées) en tant que sous-variété polyédrale (orientée) de $X$.
Les faces (i.e. les $(p-1)$-facettes) du $p$-simplexe standard $\Delta_p$ sont naturellement ordonnées : pour $1\leq i\leq p+1$, la $i^{eme}$ face de $\Delta_p$ est l’enveloppe des sommets $v^{1}_{p+1},\dots,v^{i-1}_{p+1},v^{i+1}_{p+1},\dots,v^{p+1}_{p+1}$. Ceci permet de définir une notion de $i^{eme}$ face pour un simplexe singulier, non-singulier ou plongé.
Ainsi, si $\sigma:\Delta_p\to X$ est un $p$-simplexe (non-)singulier, la $i^{ème}$ face de $\sigma$ est, par définition, la composée de la restriction de $\sigma$ à la $i^{eme}$ face de $\Delta_p$ et du paramétrage affine standard de cette dernière ; on la notera $\partial^i_p \sigma$.On étend alors par linéarité pour définir un opérateur de $i^{eme}$ face
$$\partial^i_p : C_p^{Sing}(X) \to C_{p-1}^{Sing}(X).$$
On définit alors un opérateur de bord
$$\partial_p : C_p^{Sing}(X) \to C_{p-1}^{Sing}(X)$$
en posant
$$\partial_p:=\sum_{i=1}^{p+1} (-1)^i \partial^i_p.$$
Nous laissons au lecteur le soin de vérifier que l’on a alors
$$\partial_{p-1}\circ\partial_p=0.$$
Comme les faces d’un $p$-simplexe non-singulier sont des $(p-1)$-simplexes non-singuliers, les opérateurs ci-dessus induisent par restriction des opérateurs
$$\partial^i_p : C_p^{NonSing}(X) \to C_{p-1}^{NonSing}(X)$$
et
$$\partial_p : C_p^{NonSing}(X) \to C_{p-1}^{NonSing}(X)$$
On définit maintenant un opérateur de bord
$$\partial_p : C_p^{Plonges}(X) \to C_{p-1}^{Plonges}(X)$$
comme suit. Si $V$ est un $p$-simplexe plongé dans $X$ orienté, si $\sigma:\Delta_p\to X$ est un paramétrage direct de $V$, alors $\partial_p V$ sera par définition l’image de $\Delta_q$ par $\partial_p\sigma$, muni de l’image de l’orientation standard de $\Delta_q$ par $\partial_p\sigma$. On vérifie que cette définition ne dépend pas du choix de $\sigma$. En fait, on vérifie que $\partial_p V$ n’est autre que la somme des faces de $V$ munie de leurs orientations comme bord de la variété topologique orientée à bord $V$. Il ne reste alors plus qu’à étendre $\partial_p$ à $C_p^{Plonges}(X)$ par linéarité. Bien entendu, on a ainsi $\partial_{p-1}\circ\partial_p=0.$
Notons qu’on ne peut pas définir d’opérateur de $i^{eme}$ face sur $C_p^{Plonges}(X)$. En effet, il n’y a pas d’ordre bien défini (i.e. indépendant du paramétrage) sur les faces d’un simplexe plongé.
Rappelons qu’on a également défini ici un opérateur de bord
$$\partial_p : C_p^{\square}(X) \to C_{p-1}^{\square}(X).$$
Rappelons également une nouvelle fois que $C_*^{Plongés}(X)$ s’injecte naturellement dans $C_*^\square(X)$ puisqu’un simplexe plongé est une sous-variété polyédrale. Cette injection commute avec les opérateurs de bord : si $V$ est un $p$-simplexe plongé dans $X$ orienté, le bord $V$ est le même selon qu’on voit $V$ comme simplexe plongé ou comme sous-variété polyédrale.
Bissections
Comme nous l’avons fait pour les sous-variétés polyédrales, nous devons maintenant définir une notion de subdivision pour les simplexes singuliers, non-singuliers et plongés. Par souci de simplicité, nous nous limiterons à des subdivisions particulières : celles obtenues par une suite de bissections.
Considérons des entiers $1\leq i < j\leq p+1$, et un point $v$ situé sur l’arête $[v_{p+1}^i,v_{p+1}^j]$ du simplexe géométrique standard $\Delta_p$. Pour éviter un cas particulier trivial, nous supposons que $v$ n’est pas l’une des deux extrémités de l’arête. Considérons alors les $p$-simplexes géométriques affines
$$\Delta^-:=\mathrm{Conv}(v_{p+1}^1,\dots,v_{p+1}^{j-1},v,v_{p+1}^{j+1},\dots,v_{p+1}^{p+1})$$
et
$$\Delta^+:=\mathrm{Conv}(v_{p+1}^1,\dots,v_{p+1}^{i-1},v,v_{p+1}^{i+1},\dots,v_{p+1}^{p+1}).$$
On remarque que $\Delta^-$ et $\Delta^+$ sont obtenus en coupant le simplexe standard $\Delta_p$ le long de l’hyperplan passant par $v$ et par les $p-1$ sommets de $\Delta_p$ différents de $v_{p+1}^i$ et $v_{p+1}^j$.
Nous appellerons paramétrage affine standard de $\Delta^-$ la bijection affine de $\Delta_p$ sur $\Delta^-$ qui fixe les $p$ sommets communs à $\Delta_p$ et $\Delta^-$ (c’est-à-dire qui fixe $v_{p+1}^k$ pour $k\neq j$) et qui envoie $v_{p+1}^j$ sur $v$. De même, nous appellerons paramétrage affine standard de $\Delta^+$ la bijection affine de $\Delta_p$ sur $\Delta^+$ qui fixe les $p$ sommets communs à $\Delta_p$ et $\Delta^+$ (c’est-à-dire qui fixe $v_{p+1}^k$ pour $k\neq i$) et qui envoie $v_{p+1}^i$ sur $v$.
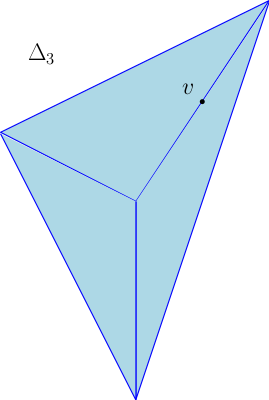
- Le $3$-simplexe géométrique standard, et un point $v$ sur une arête de ce $3$-simplexe
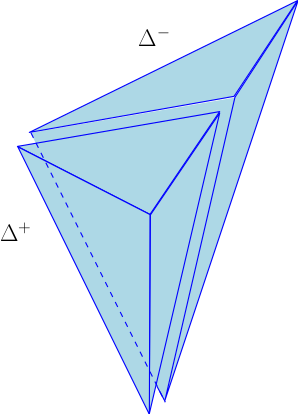
- La bissection de $\Delta_3$ associée au point $v$
Soit $\sigma:\Delta_p\to X$ un $p$-simplexe singulier. Notons $\sigma^-:\Delta_p\to X$ (resp. $\sigma^+:\Delta_p\to X$) le $p$-simplexe singulier obtenu par composition du paramétrage affine standard de $\Delta^-$ (resp. $\Delta^+$) et de la restriction de $\sigma$ à $\Delta^-$ (resp. $\Delta^+$). Nous dirons que la somme formelle $\sigma^-+\sigma^+\in C_p^{Sing}(X)$ est une bissection linéaire du simplexe singulier $\sigma$. Plus précisément, c’est la bissection associée au point $v$.
Dans le cas particulier où $\sigma$ est un $p$-simplexe non-singulier, alors $\sigma^-$ et $\sigma^+$ sont eux aussi des $p$-simplexes non-singuliers. La bissection $\sigma^-+\sigma^+$ appartient alors à $C_p^{NonSing}(X)$.
Il devrait être clair pour le lecteur qu’une bissection d’un simplexe singulier est engendrée par une bissection d’une arête de celui-ci, et que, réciproquement, toute bissection d’une arête d’un simplexe singulier engendre une bissection de ce dernier. Nous précisons tout cela dans le bloc déroulant ci-dessous, qui peut-être omis en première lecture.
Soit $\sigma:\Delta_q\to X$ un $q$-simplexe, et $\sigma':=\sigma^-+\sigma^+$ une bissection de $\sigma$. Par définition, cette bissection est associée à un point $v$ situé sur une arête $A$ du simplexe géométrique standard $\Delta_q$. Notons $\theta_A:\Delta_1\to A$ le paramétrage affine standard de cette arête $A$, et considérons le point $\hat v:=\theta_A^{-1}(v)\in \Delta_1$. Le $1$-simplexe $\epsilon:=\sigma_{|A}\circ\theta_A:\Delta_1\to X$ est une arête (i.e. une $1$-facette) du simplexe singulier $\sigma$. Soit $\epsilon'=\epsilon^-+\epsilon^+$ la bissection de $\epsilon$ associée au point $\hat v$. L’arête $\epsilon$ et la bissection $\epsilon'$ de cette arête sont uniquement déterminées par la bissection $\sigma'$ du $q$-simplexe $\sigma$. Réciproquement, connaissant $\sigma$ et $\epsilon$, la bissection $\sigma'$ est entièrement déterminée par le point $\hat v$, et donc entièrement déterminée par la bissection $\epsilon'$. Nous dirons donc que la bissection de $\sigma'$ du $q$-simplexe $\sigma$ est engendrée de la bissection $\epsilon'$ de l’arête $\epsilon$.
Considérons maintenant une $p$-chaîne $\gamma$, une $q$-facette $\sigma$ de $\gamma$ et une bissection $\sigma'$ de $\sigma$. Comme nous venons de l’expliquer, cette bissection est engendrée par une bissection $\epsilon'$ d’une arête $\epsilon$ de $\sigma$. Considérons maintenant la $p$-chaîne $\gamma'$ obtenue à partir de $\gamma$ par la procédure suivante : pour tout $p$-simplexe $\tau$ de $\gamma$, si $\epsilon$ est une arête de $\tau$, alors on remplace $\tau$ par la bissection $\tau'$ de $\tau$ engendrée par la bissection $\epsilon'$ de $\epsilon$. Nous dirons que la $p$-chaîne $\gamma'$ est la bissection complète de $\gamma$ engendrée par la bissection $\sigma'$ de $\sigma$.
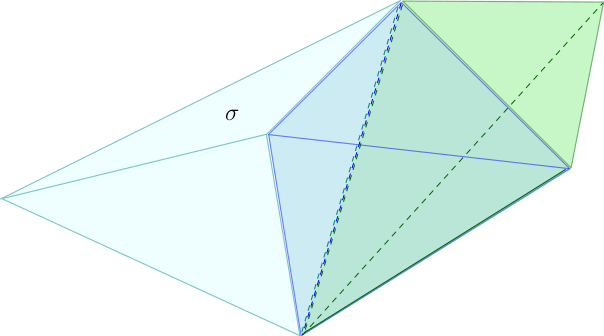
- Une $3$-chaîne $\gamma$ (constituée de trois $3$-simplexes) et une $2$-facette $\sigma$ de cette $3$-chaîne
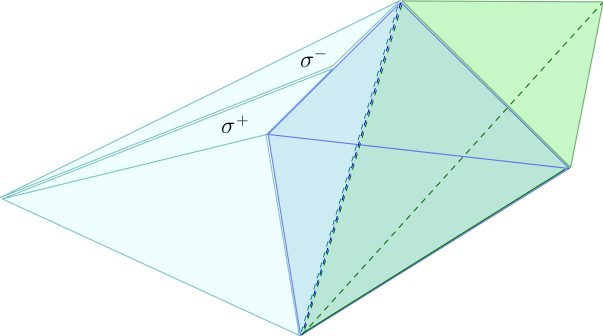
- Une bissection $\sigma^-+\sigma^+$ de la $2$-facette $\sigma$
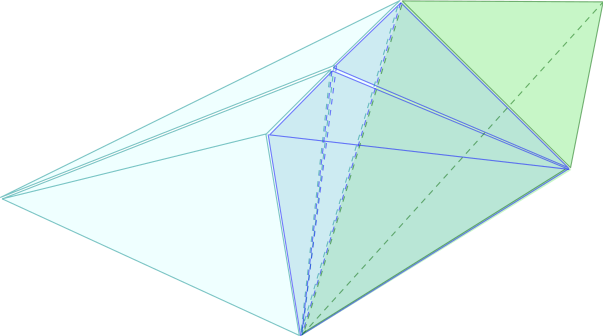
- La bissection complète de $\gamma$ engendrée par la bissection $\sigma^-+\sigma^+$ de $\sigma$
Cette notion de « bissection complète engendrée » se comporte bien vis-à-vis de l’opérateur bord. Plus précisément, elle satisfait la propriété suivante, dont nous laissons la preuve au lecteur :
Soient $\alpha$ une $p$-chaîne singulière et $\beta=\partial_p\alpha$. Soient $\sigma$ une $q$-facette de $\beta$ (donc aussi de $\alpha$), et $\sigma'$ une bissection de $\sigma$. On note $\alpha'$ (resp. $\beta'$) la bissection complète de $\alpha$ (resp. $\beta$) engendrée par la bissection $\sigma'$ de $\sigma$. Alors $\beta'=\partial_p \alpha'$.
Soit maintenant $V$ un $p$-simplexe plongé dans $X$. Soit $w$ un point d’une arête de $V$ qui ne soit pas une des deux extrémités de cette arête. Soit $\sigma:\Delta_p\to X$ un paramétrage non-singulier de $V$ et $v:=\sigma^{-1}(w)$. Par définition, $\sigma$ est un simplexe non-singulier et $v$ est un point situé sur une arête du simplexe standard $\Delta_p$. On peut donc considérer la bissection $\sigma^-+\sigma^+$ de $\sigma$ associée au point $v:=\sigma^{-1}(w)$, comme définie ci-dessus. On pose alors $V^-=\sigma^-(\Delta_p)$ et $V^+=\sigma^+(\Delta_p)$. et on dit que la somme formelle $V^-+V^+\in C_p^{Plonges}(X)$ est la bissection linéaire de $V$ associée au paramétrage $\sigma$ et au point $v$.
Notons que, si $V^-+V^+$ est une bissection linéaire du simplexe plongé $V$, alors $V^-$ et $V^+$ sont deux $p$-simplexes plongés, d’intérieurs disjoints, qui s’intersectent le long d’une face commune, et dont l’union est égale à $V$.
Soient $\alpha,\alpha'$ deux $p$-chaînes singulières (respectivement non-singulières, plongées), c’est-à-dire deux éléments du $\mathbb{Z}$-module $C_p^{Sing}(X)$ (respectivement $C_p^{NonSing}(X)$, et $C_p^{Plonges}(X)$). On notera
$$\alpha'\preceq \alpha$$
si $\alpha'$ est obtenu par une suite de bissections des simplexes de $\alpha$. Attention, il ne s’agit pas d’une relation d’ordre : le lemme ci-dessous montre en effet que $\preceq$ n’est pas anti-symétrique. Par contre $\preceq$ est clairement compatible avec les combinaisons linéaires.
Nous utiliserons le lemme technique suivant :
Si $\alpha,\alpha_1,\alpha_2\in C_p^{Sing}(X)$ sont telles que $\alpha_1\preceq\alpha$ et $\alpha_2\preceq\alpha$, alors il existe $\alpha'$ tel que $\alpha'\preceq\alpha_1$ et $\alpha'\preceq\alpha_2$.
Informellement, ce lemme signifie que, si $\alpha_1$ et $\alpha_2$ sont deux « subdivisions par bissections successives » de $\alpha$, alors une troisième « subdivision par bissections successives » de $\alpha$ qui raffine à la fois $\alpha_1$ et $\alpha_2$. Vue notre définition des bissections, la preuve du lemme se déroule entièrement au niveau du simplexe géométrique standard $\Delta_p$. Il s’agit essentiellement de montrer que, si on a deux bissections de $\Delta_p$, alors on peut trouver une subdivision par bissections successives de $\Delta_p$ qui raffine ces deux bissections. Nous laissons les détails au lecteurs.
Il est important de remarquer que l’analogue du lemme ci-dessus pour les simplexes plongés est faux. En effet, dans ce cas, les bissections qui permettent de construire $\alpha_1$ et $\alpha_2$ peuvent provenir de paramétrages différents des simplexes de $\alpha$, et on ne peut pas nécessairement « réconcilier » ces bissections.
Nous aurons également besoin d’un second lemme technique, dans le même goût que celui ci-dessus :
Pour comprendre ce lemme, commençons par remarquer que la relation $\alpha\preceq 0$ n’implique pas nécessairement que $\alpha$ soit nul. On peut par exemple considérer un $p$-simplexe singulier $\sigma$, une bissection $\sigma^-+\sigma^+$ de $\sigma$, et la $p$-chaîne singulière $\alpha=\sigma^-+\sigma^+-\sigma$. Cette $p$-chaîne n’est pas nulle. Pourtant, on a
$$\alpha=(\sigma^-+\sigma^+)-\sigma\preceq \sigma-\sigma=0.$$
Mais on remarque alors que l’on a aussi
$$0=(\sigma^-+\sigma^+)-(\sigma^-+\sigma^+)\preceq (\sigma^-+\sigma^+)-\sigma =\alpha.$$
Nous laissons le lecteur généraliser cet exemple pour construire une preuve du lemme ci-dessus.
Nous considérons maintenant la relation d’équivalence $\sim$ sur le $\mathbb{Z}$-module $C_p^{Sing}(X)$ (respectivement $C_p^{NonSing}(X)$, et $C_p^{Plonges}(X)$) engendrée par la relation $\preceq$ : on a $\alpha\sim \alpha'$ s’il existe une suite $\alpha=\alpha_0,\alpha_1,\dots,\alpha_2k=\alpha'$ tel que
$$\alpha=\alpha_0\succeq \alpha_1 \preceq \alpha_2 \succeq \alpha_3\preceq \dots \succeq \alpha_{2k-1}\preceq \alpha_{2k}=\alpha'.$$
Grâce au lemme ci-dessus, on obtient une caractérisation plus simple de la relation $\sim$ sur
$C_p^{Sing}(X)$ et $C_p^{NonSing}(X)$ : si $\alpha,\alpha'\in C_p^{Sing}(X)$ (resp. $C_p^{NonSing}(X)$), on a $\alpha\sim \alpha'$ s’il existe $\alpha''$ tel que
$$\alpha\succeq\alpha''\preceq\alpha'.$$
Enfin, nous considérons les $\mathbb{Z}$-modules quotients
$$\begin{eqnarray*} \overline{C}{}_p^{Sing}(X) & := & C_p^{Sing}(X)/\sim \\ \overline{C}{}_p^{NonSing}(X) & := & C_p^{NonSing}(X)/\sim \\ \overline{C}{}_p^{Plonges}(X) & := & C_p^{Plonges}(X)/\sim \end{eqnarray*}$$
L’opérateur de bord défini sur $C_p^{Sing}$ (voir ci-dessus) passe au quotient en un opérateur de bord
$$\overline{\partial}_p : \overline{C}{}_p^{Sing}(X) \to \overline{C}{}_{p-1}^{Sing}(X).$$
Celui-ci envoie bien entendu le sous-module $\overline{C}_p^{NonSing}(X)$ dans $\overline{C}{}_{p-1}^{NonSing}(X)$. On obtient ainsi un opérateur de bord
$$\overline{\partial}_p : \overline{C}{}_p^{NonSing}(X) \to \overline{C}{}_{p-1}^{NonSing}(X).$$
Enfin, l’opérateur de bord défini sur $C_p^{Plongés}$ (ici) passe au quotient en un opérateur de bord
$$\overline{\partial}_p : \overline{C}{}_p^{Plonges}(X) \to \overline{C}{}_{p-1}^{Plonges}(X).$$
Groupes d’homologie singulière, non-singulière, plongée
Nous sommes maintenant prêts à définir des groupes d’homologie. Pour tout $p\in\mathbb{N}$, on définit le $p^{ème}$ groupe d’homologie singulière de $X$
$$\small{\overline{H}{}_p^{Sing}(X):=\ker\left(\overline{\partial}_p: \overline{C}{}_p^{Sing}(X) \to \overline{C}{}_{p-1}^{Sing}(X)\right)\left /\mathrm{im}\left(\overline{\partial}_{p+1}: \overline{C}{}_{p+1}^{Sing}(X) \to \overline{C}{}_{p}^{Sing}(X)\right)\right..}$$
On définit de même le $p^{ème}$ groupe d’homologie non-singulière de $X$
$$\scriptsize{\overline{H}{}_p^{NonSing}(X):=\ker\left(\overline{\partial}_p: \overline{C}{}_p^{NonSing}(X) \to \overline{C}{}_{p-1}^{NonSing}(X)\right)\left /\mathrm{im}\left(\overline{\partial}_{p+1}: \overline{C}{}_{p+1}^{NonSing}(X) \to \overline{C}{}_{p}^{NonSing}(X)\right)\right.,}$$
ainsi que le $p^{ème}$ groupe d’homologie des simplexes plongés de $X$
$$\scriptsize{\overline{H}{}_p^{Plonges}(X):=\ker\left(\overline{\partial}_p: \overline{C}{}_p^{Plonges}(X) \to \overline{C}{}_{p-1}^{Plonges}(X)\right)\left /\mathrm{im}\left(\overline{\partial}_{p+1}: \overline{C}{}_{p+1}^{Plonges}(X) \to \overline{C}{}_{p}^{Plonges}(X)\right)\right..}$$
On rappelle également que nous avons définit ici un $p^{ème}$ groupe d’homologie à la Poincaré $\overline{H}_p^{\square}(X)$, construit à partir de la notion sous-variété polyédrale de $X$.
Notre but, à partir de maintenant, est de définir des morphismes « naturels » entre les différents groupes d’homologies définis ci-dessus, puis de démontrer que ces morphismes sont bijectifs, au moins en petit degré.
Avant cela, il nous faut faire une mise au point concernant notre définition de l’homologie singulière de $X$. La définition que nous avons donnée ci-dessus du $p^{eme}$ groupe d’homologie singulière de $X$ diffère de la définition classique. Habituellement, on définit ce groupe sans quotienter le complexe de chaînes par la relation d’équivalence induite par les bissections [2]. Autrement dit, on considère d’habitude le groupe d’homologie singulière
$$\small{H_p^{Sing}(X):=\ker\left(\partial_p: C_p^{Sing}(X) \to C_{p-1}^{Sing}(X)\right)\left /\mathrm{im}\left(\partial_{p+1}: C_{p+1}^{Sing}(X) \to C_{p}^{Sing}(X)\right)\right.,}$$
(voir, par exemple, notre cours sur l’homologie singulière). Heureusement les deux définitions conduisent à des groupes isomorphes :
La projection de $C_*^{Sing}(X)$ sur $\overline{C}{}_*^{Sing}(X)$ induit un isomorphisme entre les groupes d’homologie singulière $\overline{H}{}_*^{Sing}(X)$ et $H_*^{Sing}(X)$.
Commençons par un lemme technique. On peut donner deux sens différents à l’expression « $\alpha$ est un $p$-cycle modulo bissections », selon qu’on effectue des bissections de $\alpha$ avant de prendre le bord de la $p$-chaîne ainsi obtenue, ou qu’on prend d’abord le bord de $\alpha$ et qu’on effectue ensuite des bissections de cette $(p-1)$-chaîne. Le lemme suivant nous dit que ces deux définitions possibles sont en fait équivalentes :
Soit $\alpha\in C_p^{Sing}(X)$ une $p$-chaîne singulière. On suppose que $0\preceq \partial\alpha$. Alors il existe une $p$-chaîne $\alpha'$, telle que $\alpha'\preceq\alpha$, et telle que $\partial_p \alpha'=0$.
Preuve.
Nous utilisons la notion de bissection complète d’une $p$-chaîne engendrée par une bissection d’une facette introduite dans ce bloc déroulant.
Notons $\beta:=\partial_p \alpha$. Par hypothèse, $0\preceq\beta$, c’est-à-dire que la $(p-1)$-chaîne nulle est obtenue par une suite de bissections successives de certains simplexes de $\beta$. Soit alors $\beta'$ la $(p-1)$-chaîne obtenue par les « bissections complètes de $\beta$ engendrées par cette suite de bissections ». On vérifie que $\beta’=0$. En effet, $\beta'$ est une bissection complète de la $(p-1)$-chaîne nulle. Une bissection de la chaîne nulle n’est pas toujours nulle (parce que, si on écrit $0=\sigma-\sigma$, on peut bissecter la première copie de $\sigma$ et pas la deuxième) ; par contre, une bissection complète de la chaîne nulle est toujours nulle (parce que, si on a $\sigma-\sigma$, on bissecte les deux copies de la même manière par définition d’une bissection complète).
Maintenant, on note $\alpha’$ la bissection complète de $\alpha$ engendrée par la même suite de bissections. On a bien sûr $\alpha’\preceq \alpha$ (par définition de $\alpha’$). Par ailleurs, d’après le fait sur les bissections engendrées et le bord, on a $\partial_p \alpha’=\beta’$ (le bord d’une bissection complète est la bissection complète du bord). Donc $\partial_p\alpha’=0$ et le lemme est démontré.
C.Q.F.D.
Nous aurons également besoin du lemme suivant, qui est l’analogue dans notre cadre d’un résultat classique utilisé pour démontrer le théorème des petites chaînes (le résultat classique concerne les subdivisions barycentriques, alors qu’on a utilisé ici des bissections) :
Si $\alpha,\alpha'$ sont deux $p$-cycles singuliers, c’est-à-dire deux éléments de $C_p^{Sing}(X)$ tels que $\partial_p(\alpha)=\partial_p(\alpha')=0$, et si $\alpha'\preceq\alpha$, alors $\alpha-\alpha'$ est un bord : il existe $\beta\in C_{p+1}^{Sing}$ tel que $\alpha-\alpha'=\partial_{p+1}(\beta)$.
Preuve. C’est essentiellement la même que celle de ce lemme, en remplaçant les subdivisions barycentriques par des bissections.
C.Q.F.D.
Nous sommes maintenant prêts à commencer la preuve de la proposition proprement dite. Notons $\pi_q$ la projection de $C_q^{Sing}(X)$ sur $\overline{C}_q^{Sing}(X)$.
Considérons une $p$-chaîne $\alpha\in C_p^{Sing}(X)$, et supposons que $\pi_p(\alpha)\in \ker(\overline{\partial}_p)$. Si on note $\beta:=\partial_p(\alpha)$, comme $\overline{\partial}_p\circ\pi_p=\pi_{p-1}\circ\partial_p$, on a donc $\pi_{p-1}(\beta)=0$, c’est-à-dire $\beta\sim 0$ dans $C_{p-1}^{Sing}(X)$. Nous avons vu ci-dessus que ceci équivaut à l’existence d’une chaîne $\beta'\in C_{p-1}^{Sing}(X)$ tel que $\beta\succeq\beta'\preceq 0.$ D’après le lemme sur les bissections de $0$, ceci implique que $0\preceq \beta'$. Par suite, $0\preceq \beta$. En utilisant le lemme sur les cycles modulo bissections, on en déduit qu’il existe $\alpha'' \in C_p^{Sing}(X)$, tel que $\alpha''\preceq\alpha$ (donc $\pi_p(\alpha) = \pi_p(\alpha'')$) et tel que $\partial_p^{Sing}(\alpha'')=0$, c’est-à-dire $\alpha''\in\ker\left(\overline{\partial}_p\right)$.
Ceci prouve que la projection $\pi_p$ envoie $\ker\left(\partial_p\right)$ surjectivement sur $\ker\left(\overline{\partial}_p\right)$. Par suite, $\pi_p$ induit un morphisme surjectif $(\pi_p)_*:H_p^{Sing}(X)\to \overline{H}{}_p^{Sing}(X)$.
Il reste à voir que ce morphisme est également injectif. Pour ce faire, considérons $\beta\in \ker\left(\partial_p\right)$, et supposons que (la classe de) $\pi_p(\beta)$ est nulle dans $\overline{H}{}_p^{Sing}(X)$. Ceci signifie qu’il existe $\beta'\in C_p^{Sing}(X)$ et $\alpha'\in C_{p+1}^{Sing}(X)$ tels que $\pi_p(\beta')=\pi_p(\beta)$ (autrement dit $\beta'\sim\beta$) et $\partial_{p+1}\alpha'=\beta'$. Comme nous l’avons vu ci-dessus, l’équivalence $\beta'\sim\beta$ signifie qu’il existe $\beta''$ tel que $\beta'\succeq\beta''\preceq\beta$. A priori, on n’a pas nécessairement $\partial_p\beta''=0$. Cependant, on peut bien sûr remplacer $\beta''$ par n’importe quel $\beta'''$ tel que $\beta'''\preceq\beta''$. Par ailleurs, $\partial_p\beta''$ s’obtient par bissection de $\partial_p\beta=0$. Donc $\partial_p\beta''$ est nul à une suite de bissections près. Et en utilisant à nouveau le lemme sur les cycles modulo bissections, on en déduit que l’on peut trouver $\beta'''\preceq\beta''$ tel que $\partial_p\beta'''=0$. On applique maintenant le lemme sur les bissections des cycles aux deux couples $\beta,\beta'''$ et $\beta',\beta'''$. On obtient deux $(p+1)$-chaînes $\alpha_1$ et $\alpha_2$ telle que $\partial_{p+1}(\alpha_1)=\beta-\beta'''$ et $\partial_{p+1}(\alpha_2)=\beta'-\beta'''$. On a donc
$$\partial_{p+1}(\alpha'-\alpha_2+\alpha_1)=\beta'-\beta'+\beta'''+\beta-\beta'''=\beta.$$
Ainsi, la classe de $\beta$ dans $H_p^{Sing}(X)$ est nulle, on a prouvé l’injectivité de $(\pi_p)_*$, et la proposition est démontrée.
C.Q.F.D.
L’analogue de la proposition ci-dessus, où on remplace les bissection par des subdivisions barycentriques, est faux. Le problème est que l’on n’a pas d’analogue, pour les subdivisions barycentriques, de la notion de « bissection complète engendrée par une bissection de face ». Plus précisément, on pourrait définir un analogue, mais celui-ci se comporterait mal vis-à-vis du bord.
[1] Notons $\Pi$ l’hyperplan affine de $\mathbb{R}^{n+1}$ contenant le simplexe géométrique $\Delta_p$. Une application $\sigma:\Delta_p\to X$ est un plongement lisse si elle se prolonge en une immersion lisse injective définie sur un voisinage de $\Delta_p$ dans $\Pi$.
[2] Bien sûr, le passage au quotient par les bissections dans notre définition des groupes d’homologie singulière est motivée par notre volonté de relier homologie singulière et homologie à la Poincaré.
