Définition de l’homologie à la Poincaré

Nous avons déjà décrit dans l’article précédent l’idée intuitive qui semble avoir guidé Poincaré dans sa définition de l’homologie.

On veut mesurer la complexité de la topologie d’une variété $X$ en comptant, pour chaque entier $p$ entre $0$ et $\mathrm{dim}(X)$, le nombre maximal de sous-variétés fermées de dimension $p$ que l’on peut « faire entrer » dans $X$, sans que certaines de ces sous-variétés, correctement orientées, ne forment le bord orienté d’un « morceau » de $X$ de dimension $p+1$.

Nous avons également montré, sur un exemple, qu’il convient :

• d’interpréter le terme « morceau » de $X$ en autorisant au moins des « sous-variétés » dont le bord présente de faces, d’arrêtes, et des coins ; ceci nous conduira à la notion de sous-variété polyédrale.
• de s’autoriser à subdiviser les sous-variété polyédrale.

Il est temps maintenant de mettre au point des définitions formelles.

Sous-variétés polyédrales

Rappelons tout d’abord qu’un demi-espace vectoriel fermé de $\mathbb{R}^p$ est l’adhérence d’une des deux composantes connexes du complémentaire, dans $\mathbb{R}^p$, d’un hyperplan vectoriel. Nous appellerons demi-cône vectoriel polyédral une intersection finie de demi-espaces vectoriels fermés de $\mathbb{R}^p$ (cette intersection peut être vide : par convention, $\mathbb{R}^p$ est aussi un demi-cône vectoriel polyédral). Un demi-cône polyédral est non-dégénéré s’il est d’intérieur non-vide. Si $P$ est un demi-cône vectoriel polyédral non-dégénéré dans $\mathbb{R}^p$, nous appellerons indice de $P$ la dimension du plus gros sous-espace vectoriel de $\mathbb{R}^p$ contenu dans $P$ ; c’est un entier compris au sens large entre $0$ et $p$.

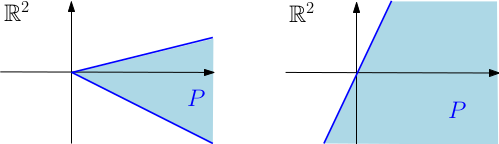
Deux demi-cônes vectoriels polyédraux non-dégénérés dans $\mathbb{ R }^2$, d’indices respectifs $0$ et $1$

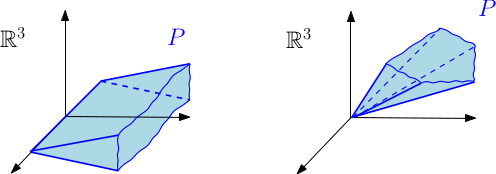
Deux demi-cônes vectoriels polyédraux non-dégénérés dans $\mathbb{R}^3$, d’indices respectifs $1$ et $0$

Par exemple, si $P$ est un polytope [2] d’intérieur non-vide dans $R^p$, alors $W:=P\times\{0_{\mathbb{R}^{n-p}}\}$ est une sous-variété polyédrale de dimension $p$ de $\mathbb{R}^n=\mathbb{R}^p\times \mathbb{R}^{n-p}$.

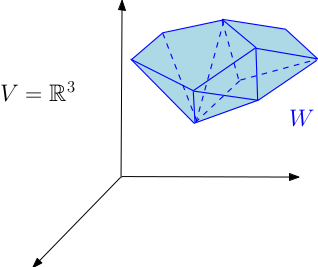
Une sous-variété polyédrale $W$ de dimension 2 dans une variété $V$ de dimension 2

Une sous-variété polyédrale de dimension 3 dans $\mathbb{R}^3$

L’indice $q$ du demi-cône $P$ qui apparait dans la définition ci-dessus dépend de la sous-variété $W$ et du point $x$, mais pas du voisinage $O$ et de la carte $\phi$. C’est une conséquence immédiate de l’invariance de l’indice d’un demi-cône vectoriel polyédral de $\mathbb{R}^p$ par difféomorphisme dans $\mathbb{R}^p$. Nous dirons que cet entier $q$ est l’indice du point $x$.

Par exemple, si $W$ est une sous-variété à bord « classique » de dimension $p$, alors $W$ n’a aucune $q$-facette pour $k\leq p-2$, et les $(p-1)$-facettes de $W$ sont ses composantes de bord. Si $W$ est un polytope dans $\mathbb{R}^n$, alors les $q$-facettes de $W$ au sens classique (pour les polytopes) coïncident exactement avec les $q$-facettes de $W$ vues comme sous-variété polyédrale.

Nous laissons le lecteur le soin de démontrer le lemme suivant en guise d’exercice :

Comme pour les sous-variétés et les sous-variétés à bords classiques, on peut définir une notion d’orientation pour les sous-variétés polyédrales. De plus, les faces (i.e. les $(p-1)$-facettes) d’une sous-variété polyédrale orientée de dimension $p$ héritent d’une orientation naturelle, définie exactement comme l’orientation naturelle du bord d’une sous-variété à bord.

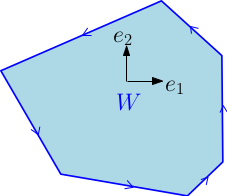
Orientation des $1$-faces d’une variété polyédrale de dimension 2

Subdivisions des variétés polyédrales

Comme expliqué précédemment, nous devons nous autoriser à « découper les sous-variétés en morceaux ». La notion de sous-variété polyédrale nous permet de donner facilement un sens à cette expression. On fixe une variété $X$ de dimension $n$.

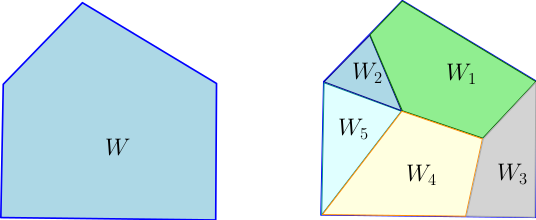
Une sous-variété polyédrale de dimension 2 dans $\mathbb{R}^2$ et une subdivsion de cette sous-variété

Dans la définition de l’homologie « à la Poincaré » que nous donnons ci-dessous, nous nous autorisons à remplacer une sous-variété polyédrale $W$ par n’importe quelle subdivision $W_1+\dots+W_\ell$ de $W$. Nous expliquerons ci-dessous, pourquoi cela est absolument nécessaire si on veut obtenir une théorie homologique raisonnable.

On considère une sous-variété polyédrale orientée $W$ de dimension $p$ de $X$, et une subdivision $W_1+\dots+W_\ell$ de $W$. Une face de la subdivision $W_1+\dots+W_\ell$, c’est-à-dire une face de l’une des sous-variétés $W_1,\dots,W_\ell$, est dite :

• extérieure si c’est une face d’une seule des sous-variétés $W_1,\dots,W_\ell$ ;
• intérieure si c’est une face d’au moins deux des sous-variétés $W_1,\dots,W_\ell$.

La preuve du lemme suivant (qui est évident sur un dessin ; voir la figure ci-dessus) est laissée au lecteur :

Définition des groupes d’homologie à la Poincaré

Comme expliqué dans l’introduction de la rubrique, Riemann et Betti avaient déjà imaginé mesurer la complexité de la forme d’une variété $X$ en cherchant le nombre maximal $b_p(X)$ de sous-variétés fermées de dimension $p$ de $X$ qui ne forment le bord d’aucune sous-variété à bord de dimension $p+1$. C’est pourquoi l’entier $b_p(X)$ s’appelle le $p^\mathrm{ième}$ nombre de Betti de $X$. Les esquisses de définitions de l’entier $b_p(X)$ par Riemann et Betti restaient cependant très vagues. Poincaré a réussi élaborer une définition formelle essentiellement correcte de $b_p(X)$. Mais il est aussi compris qu’on pouvait ainsi associer à la variété $X$ beaucoup plus qu’un simple entier. Il considère l’ensemble des combinaisons linéaires de sous-variétés de dimension $p$ modulo les bords de sous-variétés de dimension $p+1$. On obtient ainsi un $\mathbb{Z}$-module associée à la variété $X$. Poincaré ne sait pas définir formellement cet objet algébrique, car il ne dispose pas du concept d’ensemble quotient qui ne se banalisera qu’au milieu du XXème siècle. Cela ne l’empêche pas d’en décrire entièrement la structure (partie libre, partie de torsion,...) dans son Second Complément à l’Analysis Situs (voir également nos commentaires). L’entier $b_p(X)$ recherché n’est autre que le rang de ce $\mathbb{Z}$-module.

Aujourd’hui, il est devenu naturel de formaliser les idées de Poincaré comme suit.

Soit $X$ une variété de dimension $n$. Pour tout entier $p\in\{0,\dots,n\}$, on note $C_p^\square(X)$ le $\mathbb{Z}$-module libre engendré par toutes les sous-variétés polyédrales orientées connexes de dimension $p$ de $X$, quotienté afin que $-W$ et $W$ représentent la même sous-variété munie de deux orientations opposées [3]. On étend cette définition aux valeurs de $p$ supérieures à $n$ en posant $C_p^\square(X)=\{0\}$ pour $p>n$ (c’est naturel puisqu’une sous-variété de $X$ est nécessairement de dimension inférieure ou égale à $n=\mathrm{dim}(X)$).Les éléments de $C_p^\square(X)$ sont donc des combinaisons linéaires formelles, à coefficients entiers, de sous-variétés polyédrales orientées de $V$.

On peut alors définir, pour $p$, un opérateur de bord

$$\partial_p : C_p^\square(X) \longrightarrow C_{p-1}^\square(X)$$

comme suit :

• l’image par $\partial_p$ d’une sous-variété orientée $W$ de dimension $p$ est la somme formelle des faces de $W$ (munies de leur orientation naturelle) ;
• on étend alors $\partial_p$ à $C_p^\square(X)$ par linéarité.

Il nous faut tenir compte des subdivisions. On considère la relation d’équivalence $\sim$ sur $C_p^\square(X)$ la moins fine telle que :

• $W\sim W_1+\dots+W_\ell$ pour toute subdivision $W_1+\dots+W_\ell$ de $W$,
• $\sim$ est compatible avec les opérations de combinaisons linéaires.
• On considère alors le quotient

  $$\overline{C}{}_p^\square(X):=C_p^\square(X)/\sim.$$

Puisque $\sim$ est compatible avec les opérations de combinaisons linéaires, c’est encore un $\mathbb{Z}$-module. Mais ce $\mathbb{Z}$-module n’a aucune raison d’être libre [4].

Du lemme sur les faces d’une subdivision, on déduit immédiatement que l’opérateur de bord $\partial_p : C_p^\square(X) \longrightarrow C_{p-1}^\square(X)$ passe au quotient en un opérateur de bord

$$\overline{\partial}_p : \overline{C}{}_p^\square(X) \longrightarrow \overline{C}{}_{p-1}^\square(X).$$

Les éléments de $\overline{C}{}_p^\square(X)$ sont appelés des $p$-chaînes. On dit qu’une $p$-chaîne $C$ est :

• un cycle si son bord est nul, c’est-à-dire si elle appartient à $\ker\overline{\partial}_p$ ;
• un bord si elle est le bord d’une $p+1$-chaîne, c’est-à-dire si elle appartient à $\mathrm{im}(\overline{\partial}_{p+1})$.

En utilisant le lemme sur les faces d’une subdivision, on montre facilement :

Ceci nous permet de définir des groupes d’homologies :

L’entier $b_p^\square(X)$ est donc le cardinal maximal d’une famille de combinaisons linéaires sans bords de sous-variétés polyédrales orientées de dimension $p$ qui n’est pas --- à subdivision près --- le bord d’une combinaison linéaire de sous-variétés polyédrales orientée de dimension $p+1$. On peut donc considérer cet entier $b_p^\square(X)$ comme la mesure de la complexité de la topologie de la variété $X$ évoquée dans l’idée intuitive au début de cet article.

Pourquoi est-il nécessaire de s’autoriser à subdiviser ?

Comme nous l’avons signalé dans nos commentaires, Poincaré n’évoque jamais la nécessité de « quotienter par l’opération de subdivision » (même si nous pensons qu’il le fait tacitement). De fait, on aurait très bien pu définir des groupes d’homologies sans quotienter au préalable les modules $C_p^\square(X)$ par la relation de subdivision $\sim$. Autrement dit, on aurait pu considérer, pour tout $p$ ; le module

$$H_p^\square(X):=\ker\left(\partial_p : C_p^\square(X) \longrightarrow C_{p-1}^\square(X)\right)\left/\mathrm{im}\left(\partial_{p+1} : C_{p+1}^\square(X) \longrightarrow C_{p}^\square(X)\right)\right..$$

au lieu du module

$$\overline{H}_p^\square(X):=\ker\left(\overline{\partial}_p : \overline{C}{}_p^\square(X) \longrightarrow \overline{C}{}_{p-1}^\square(X)\right)\left/\mathrm{im}\left(\overline{\partial}_{p+1} : \overline{C}{}_{p+1}^\square(X) \longrightarrow \overline{C}{}_{p}^\square(X)\right)\right..$$

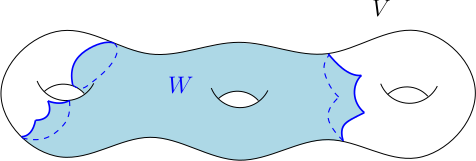
Cette définition plus simple est d’autant plus tentante que, dans de nombreuses situations, les subdivisions « se font naturellement sans qu’on soit obligé de les forcer à apparaître ». Considérons, par exemple, une courbe fermée simple $C$ dans le tore $\mathbb{T}^2$, et une subdivision $A_1,A_2,A_3$ de $C$ (les $A_i$ sont des arcs). La figure ci-dessous montre comment trouver des sous-variétés polyédrales $S,S_1,\dots,S_3$ de dimension deux de $\mathbb{T}^2$, tel que

$$\begin{eqnarray*} && \partial_2\left(S-\left(S_1+S_2+S_3\right)\right) \\ & =& C-A_1'-A_2'-A_3'-\left(\left(A_1-A_1'\right)+\left(A_2-A_2'\right)+\left(A_3-A_3'\right)\right) \\ & = & C-(A_1+A_2+A_3). \end{eqnarray*}$$

Ainsi, la courbe $C$ est égale à $A_1+A_2+A_3$ dans le module $H_1^\square\left(\mathbb{T}^2\right)$ (alors même qu’on n’a pas tenu compte des subdivisions pour définir $H_1^\square(\mathbb{T}^2)$). On en déduit que $H_1^\square\left(\mathbb{T}^2\right)=\overline{H}{}_1^\square\left(\mathbb{T}^2\right)$.

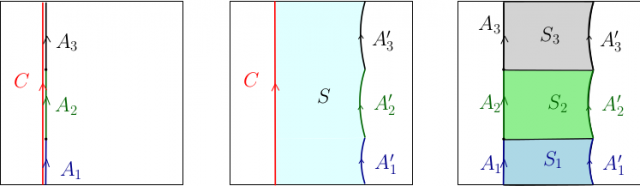
Homologie entre une courbe fermée simple et une subdivision de cette courbe

La même construction fonctionne dans n’importe quelle variété $X$. On a donc $H_1^\square(X)=\overline{H}{}_1^\square(X)$. pour toute variété $X$. Nous laissons le lecteur montrer, par une construction similaire, que l’on a également $H_{n-1}^\square(X)=\overline{H}{}_{n-1}^\square(X)$ si $\mathrm{dim}(X)=n$. Notons que cela implique que, si $\mathrm{dim}(X)\leq 3$, alors on a $H_{p}^\square(X)=\overline{H}{}_{p}^\square(X)$ pour tout $p$, sauf peut-être $p=\mathrm{dim}(X)$ (qui n’est certainement pas la valeur de $p$ qui nous intéresse le plus).

Hélas... hélas... ça se gâte quand on considère des variétés de dimension supérieure. Si on ne tient pas compte des subdivisions dans la définition de l’homologie, on trouve une complexité infinie même pour certaines variétés parmi les plus simples ! Par exemple, si $p$ de la forme $2^s$ et si $X$ est une variété de dimension $4p-1$, le groupe d’homologie $H_p^\square(X)$ n’est pas dénombrablement engendré. En particulier, $H_p^\square\left(\mathbb{R}^{4p-1}\right)$ n’est pas dénombrablement engendré ! (alors que le groupe d’homologie à la Poincaré $\overline{H}_p^\square\left(\mathbb{R}^n\right)$ est trivial, pourvu que $p<7$, voir ici).

Considérons une sous-variété compacte sans bord $W$ de dimension $p$ d’une variété $X$. En particulier, $W$ est un élément $C_p(X)$ de bord nul (i.e. un $p$-cycle). Supposons que $W$ est homologue, dans $H_p^\square(X)$, à un autre $p$-cycle $W'$. Alors $W$ sera une face d’une sous-variété polyédrale $V$ de dimension $p+1$. Quitte à munir $X$ d’une métrique riemannienne, on peut alors considérer, en tout point de $W$, le vecteur unitaire tangent à $V$, normal à $W$, dirigé vers l’extérieur de $V$. Ceci fournit un champ de vecteur le long de $W$, normal à $W$, et qui ne s’annule pas (autrement dit, une section du fibré normal à $W$ qui ne s’annule pas).

Or on sait que :

• si on a un plongement de l’espace projectif complexe $\mathbb{CP}^{p}$ dans une variété (réelle) de dimension (réelle) $4p-1$, alors toute section du fibré normal à ce plongement s’annule (voir [5]) ;
• si $p$ est de la forme $2^s$, on peut plonger l’espace projectif complexe $\mathbb{CP}^{p}$ dans $\mathbb{R}^{4p-1}$ (voir [6]).

Pour $p=2^s$, considérons l’image $W$ d’un plongement $\mathbb{CP}^{p}$ dans $\mathbb{R}^{4p-1}$. D’après ce qui précède, toute section du fibré normal de $W$ s’annule, et ceci implique que $W$ n’est homologue, dans $H_p^\square(\mathbb{R}^{4p-1})$, à aucun autre $p$-cycle. Bien sûr, l’image de $W$ par n’importe quel difféomorphisme de $\mathbb{R}^{4p-1}$ vérifiera la même propriété. Comme l’ensemble des difféomorphismes de $\mathbb{R}^{4p-1}$ qui ne fixent pas $W$ est évidemment de cardinal non-dénombrable, on en déduit que le groupe d’homologie $H_p^\square\left(\mathbb{R}^{4p-1}\right)$ au sens défini ci-dessus sera de rang non-dénombrable !

De plus, comme le fibré normal d’une sous-variété $W$ ne dépend que d’un voisinage de $W$ dans la variété ambiante, et comme tout variété de dimension $n$ est localement difféomorphe à $\mathbb{R}^n$, on en déduit que, pour $p=2^s$, le groupe d’homologie $H_p^\square(X)$ n’est dénombrablement engendré pour aucune variété $X$ de dimension $4p-1$.