
|
> Homologie > L’homologie "à la Poincaré" > Comparaison entre homologie à la Poincaré et homologie singulière > Trivialité de l’homologie de l’espace affine II Trivialité de l’homologie de l’espace affine II |
Dans notre article précédent, on a ramené la trivialité des groupes d’homologie de $\mathbb{R}^n$ en degré plus petit que $7$ à la proposition suivante :
Un $p$-cycle non-singulier $\omega$ à valeurs dans $\mathbb{R}^n$ étant fixé, pour tout $p$-cycle non-singulier $\omega'$ ayant les mêmes relations d’incidence que $\omega$, et suffisamment proche de $\omega$, la différence $\omega'-\omega$ est le bord d’une $(p+1)$-chaîne non-singulière.
Nous allons maintenant démontrer cette proposition. La preuve consiste à pousser chaque facette de $\omega'$ vers la facette correspondante dans $\omega$, en commençant par les $0$-facettes (les sommets), puis les $1$-facettes, etc., jusqu’aux $p$-facettes (les $p$-simplexes constituant $\sigma$). Pour réaliser cette opération, on introduit une déformation des simplexes.
Déformations de simplexes
Étant donné un $p$-simplexe non-singulier $\sigma$ à valeurs dans $\mathbb{R}^n$, une $q$-facette $\eta$ de $\sigma$, et un $q$-simplexe non-singulier $\eta'$ proche de $\eta$, nous allons définir une déformation $\sigma'=\Phi_{\eta}^{\eta'}(\sigma)$ du $p$-simplexe $\sigma$ telle que $\eta'$ soit une $q$-facette de $\sigma'$. On veut que l’opération de déformation qui à $\sigma$ et $\eta'$ associe le simplexe $\sigma'$ possède certaines propriétés, en particulier qu’elle « commute avec l’opérateur de bord ». Autrement dit, on veut que les facettes du simplexe déformé $\sigma'$ coïncide avec les déformations des facettes de $\sigma$.
Pour définir précisément l’opération de déformation des simplexes, on a besoin d’introduire quelques notations. Soit $\Delta$ un $p$-simplexe géométrique affine (dans un espace affine $E$), et $\delta$ une $q$-facette de $\Delta$, avec $q < p$. Rappelons que cela signifie que $\Delta$ est l’enveloppe convexe de $p+1$ points affinement indépendants de $E$, et que $\delta$ est l’enveloppe convexe de $q+1$ de ces points. Notons $\hat\delta$ la $(p-q)$-facette de $\Delta$ opposée à $\delta$, autrement dit, l’enveloppe convexe des sommets de $\Delta$ qui ne sont pas des sommets de $\delta$. On a alors projection naturelle $\pi_{\Delta,\delta}:\Delta\setminus\hat\delta\to\delta$ : le projeté d’un point $x$ est l’unique point d’intersection de la facette $\delta$ avec le $(p-q+1)$-plan affine engendré par $\hat\delta$ et $x$. De même, on a une projection naturelle $\pi_{\Delta,\hat\delta}:\Delta\setminus\delta\to\hat\delta$. De plus, pour tout $x\in\Delta\setminus(\delta\cup\hat\delta)$, il existe un unique réel $t_{\Delta,\delta}(x)\in [0,1]$ tel que
$$x=t_{\Delta,\delta}(x).\pi_{\Delta,\delta}(x)+(1-t_{\Delta,\delta}(x)).\pi_{\Delta,\hat\delta}(x).$$
On prolonge la fonction $t_{\Delta,\delta}$ à $\Delta$ en posant $t_{\Delta,\delta}(x)=1$ si $x\in\delta$ et $t_{\Delta,\delta}(x)=0$ si $x\in\hat\delta$.
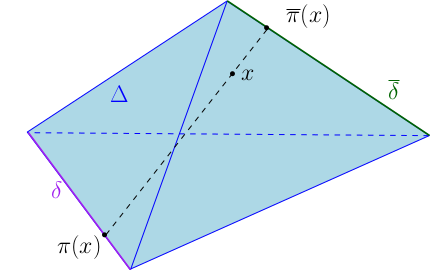
- Projections d’un $3$-simplexe géométrique $\Delta$ sur une de ses facettes $\delta$, et sur la facette opposée $\bar\delta$
L’opérateur $(\Delta,\delta)\mapsto t_{\Delta,\delta}$ est compatible avec l’opérateur de bord : si $\Delta'$ est une facette de $\Delta$ qui rencontre $\delta$ et $\hat\delta$, alors la restriction de $t_{\Delta,\delta}$ à $\Delta'$ n’est autre que la fonction $t_{\Delta',\Delta'\cap\delta}$.
On choisit une fois pour toute une fonction $\varphi:[0,1]\to [0,1]$, lisse, croissante, égale à $0$ sur un voisinage de $0$, et égale à $1$ sur un voisinage de $1$.
Considérons un $p$-simplexe non-singulier $\sigma$ à valeurs dans $\mathbb{R}^n$, une $q$-facette $\eta$ de $\sigma$, et un $q$-simplexe non-singulier $\eta'$ proche de $\eta$, avec $q < p$. Rappelons que $\sigma$ est un plongement du $p$-simplexe géométrique standard $\Delta_p$, et qu’il existe une $q$-facette géométrique $\delta$ de $\Delta_p$ tel que $\eta$ est la composée de la restriction de $\sigma$ à $\delta$ de $\Delta_p$ et du paramétrage affine canonique de $\delta$ [1]. On définit alors un $p$-simplexe singulier
$$\sigma'=\Phi_{\eta}^{\eta'}(\sigma):\Delta_p\to\mathbb{R}^n$$
par la formule :
$$\Phi_{\eta}^{\eta'}(\sigma)(x)=\sigma(x)+\varphi\left(t_{\Delta_p,\delta}(x)\right).(\eta'-\eta)\left(\pi_{\Delta_p,\delta}(x)\right).$$
Cette application est un plongement — et donc un $p$-simplexe non-singulier — dès lors que $\eta'$ est assez proche de $\eta$ ; dans la suite, nous supposerons que c’est le cas. On dira que $\sigma'$ est obtenu par déformation de $\sigma$ en poussant $\eta$ sur $\eta'$.
Dans les figures ci-dessous, et toutes celles qui suivent, pour représenter un $p$-simplexe non-singulier $\sigma:\Delta_p\to\mathbb{R}^n$, on ne dessinera que l’image $\sigma(\Delta_p)\subset\mathbb{R}^n$ de ce simplexe (à défaut de pouvoir faire mieux). Et, pour alléger les figures, on écrira simplement $\sigma$ au lieu $\sigma(\Delta_p)$.
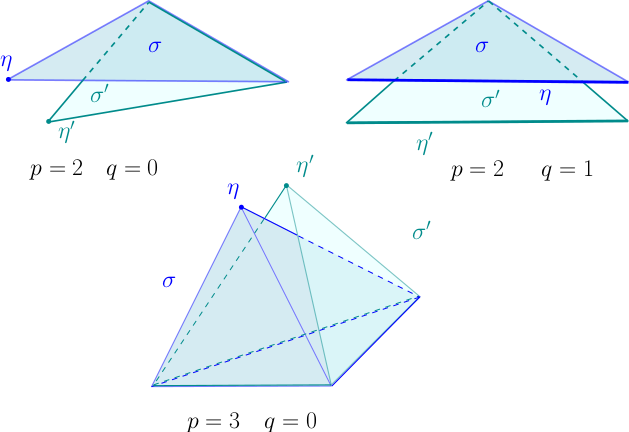
- La déformation de $\sigma$ en $\sigma':=\Phi_\eta^{\eta'}(\sigma)$ pour différentes valeurs de $p=\mathrm{dim}(\sigma)=\mathrm{dim}(\sigma')$ et $q=\mathrm{dim}(\eta)=\mathrm{dim}(\eta')$
Nous avons besoin de définir une déformation $\sigma'=\Phi_{\eta}^{\eta'}(\sigma)$ dans une situation plus générale que celle considérée ci-dessus.
Considérons un $p$-simplexe non-singulier $\sigma$ et un $q$-simplexe non-singulier $\eta$, tous deux à valeurs dans $\mathbb{R}^n$. On suppose que $\sigma$ et $\eta$ soit n’ont aucune facette commune, soit s’intersectent le long d’une $r$-facette commune $\theta$ (voir la définition), avec $r < p$. On considère un $q$-simplexe non-singulier $\eta'$ proche de $\eta$. Nous allons définir un $p$-simplexe singulier
$$\sigma'=\Phi_{\eta}^{\eta'}(\sigma):\Delta_p\to\mathbb{R}^n.$$
- Dans le cas où $\sigma$ et $\eta$ n’ont aucune facette commune, on pose simplement $\sigma':=\sigma$.
- Dans le cas où $\theta=\eta$, c’est-à-dire où $\eta$ est une $q$-facette de $\sigma$, le $p$-simplexe $\sigma'$ a déjà été défini ci-dessus.
- Dans le cas général, on note $\theta'$ la $r$-facette de $\eta'$ correspondant à $\theta$ (voir la définition). Puisque $\theta$ est une $r$-facette de $\sigma$, la déformation $\Phi_{\theta}^{\theta'}(\sigma)$ a déjà été définie ci-dessus. On peut donc poser
$$\sigma'=\Phi_\eta^{\eta'} (\sigma):=\Phi_{\theta}^{\theta'}(\sigma).$$
Le $p$-simplexe $\sigma'$ est non-singulier dès lors que $\eta'$ est suffisamment proche de $\eta$ ; dans la suite, nous supposerons toujours que c’est le cas. Comme précédemment, on dira que $\sigma'$ est obtenu par déformation de $\sigma$ en poussant $\eta$ sur $\eta'$.
Avec les notations ci-dessus, $\theta'$ est une $r$-facette du simplexe déformé $\sigma'=\Phi_{\eta}^{\eta'}(\sigma)$. Par ailleurs, les $(p-r)$-facettes de $\sigma$ et $\sigma'$ opposées respectivement aux facettes $\theta$ et $\theta'$ coïncident. Notons également que le simplexe $\Phi_{\eta}^{\eta'}(\sigma)$ dépend continûment de $\eta'$ et coïncide avec $\sigma$ si $\eta'=\eta$.
On étend maintenant l’opérateur de déformations aux chaînes.
On étend l’opérateur $\Phi_{\eta}^{\eta'}$ aux $p$-chaînes par linéarité : si $\omega=\sum \lambda_i.\sigma_i$ est une $p$-chaîne non-singulière telle que, pour chaque $i$, la déformation $\sigma_i':=\Phi_{\eta}^{\eta'}(\sigma_i)$ est bien définie, on pose
$$\Phi_{\eta}^{\eta'}(\omega):=\sum \lambda_i.\Phi_{\eta}^{\eta'}(\sigma_i).$$
La propriété ci-dessous indique que « l’opération de déformation commute avec l’opérateur de bord ». Elle jouera un rôle crucial dans la suite. Elle découle de la définition de l’opérateur de déformation et de la remarque sur l’opérateur $(\Delta,\delta)\mapsto t_{\Delta,\delta}$.
Soit $\sigma$ un $p$-simplexe non-singulier, $\eta$ un $q$-simplexe non-singulier, et $\eta'$ un $q$-simplexe non-singulier proche de $\eta$, tous trois à valeurs dans $\mathbb{R}^n$. Soit $\tau$ une $s$-facette du $p$-simplexe $\sigma$, et $\tau'$ la $s$-facette correspondante du simplexe déformé $\Phi_{\eta}^{\eta'}(\sigma)$. On pose $\theta:=\tau\cap\eta$, et on suppose que $\tau$ n’est pas contenue dans $\theta$.
- Si $\tau$ ne rencontre pas $\eta$, alors $\tau'=\tau=\Phi_{\eta}^{\eta'}(\tau)$.
- Si $\tau$ rencontre $\eta$, alors $\theta=\tau\cap\eta$ est une facette de $\eta$. Notons $\theta'$ la facette correspondante dans $\eta'$. Alors on a $\tau'=\Phi_{\theta}^{\theta'}(\tau)=\Phi_\eta^{\eta'}(\tau)$.
Par conséquent, pour toute $p$-chaîne $\omega$, la $p$-chaîne $\Phi_{\eta}^{\eta'}(\omega)$ a les mêmes relations d’incidence que $\omega$. En particulier, on a $\partial \Phi_{\eta}^{\eta'}(\omega)=\Phi_{\eta}^{\eta'}(\partial\omega)$.
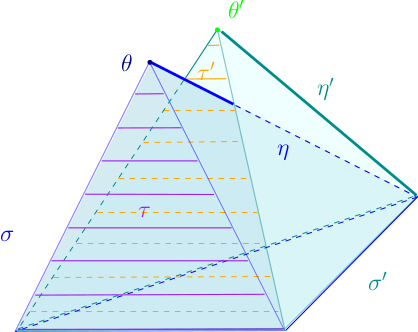
- Illustration de la propriété 1
La propriété ci-dessous (qui découle directement de la définition de l’opérateur de déformation) permet d’effectuer plusieurs déformations de simplexes successives :
Si $\eta$ est une $q$-facette d’un $p$-simplexe non-singulier $\sigma$ à valeurs dans $\mathbb{R}^n$ avec $q < p$, et si $\eta',\eta''$ sont deux $q$-simplexes non-singuliers proches de $\eta$, alors
$$\Phi_{\eta}^{\eta''}(\sigma)=\Phi_{\eta'}^{\eta''}(\Phi_{\eta}^{\eta'}(\sigma)).$$
Chaînes étoilées
Pour démontrer la Proposition clé, on sera amené à effectuer une suite d’opérations du type suivant. On considérera une $p$-chaîne non-singulière $\omega=\sum \sigma_j$, une $q$-facette $\eta$ de $\omega$ (c’est-à-dire une $q$-facette d’un des simplexes $\sigma_1,\sigma_2,\dots$), et un $q$-simplexe non-singulier $\eta'$ proche de $\eta$. On voudra alors déformer $\sigma$ en poussant $\eta$ sur $\eta'$ (à l’aide de l’opérateur de déformation défini ci-dessus).
Afin de rester dans un cadre où ce type de déformation est bien défini, nous devrons nous intéresser à des $p$-chaînes non-singulières constituées de simplexes qui ont une $q$-facette $\eta$ en commun, que nous nommerons chaînes étoilées [2].
Soient $p,q$ deux entiers tels que $0\leq q\leq p\leq n$, et $\eta$ un $q$-simplexe non-singulier. Une $p$-chaîne non-singulière étoilée de centre $\eta$ est une $p$-chaîne non-singulière $\zeta=\sum_{j} \sigma_j$ telle que $\eta$ est une $q$-facette de $\sigma_j$ pour tout $j$. Une $p$-chaîne non-singulière étoilée $\zeta$ de centre $\eta$ est dite enveloppante si $\eta$ n’est pas une facette de la $(p-1)$-chaîne $\partial \zeta$.
Dans le cas particulier où $q=p$, les seules $p$-chaînes non-singulières étoilées de centre $\eta$ sont les multiples du $p$-simplexe $\eta$. Bien sûr, si $\omega$ est une $p$-chaîne non-singulière et $\eta$ est une $q$-facette de $\sigma$, alors l’étoile de $\eta$ dans $\omega$ (c’est-à-dire la somme des $p$-simplexes de $\omega$ dont $\eta$ est une facette) est une $p$-chaîne non-singulière étoilée de centre $\eta$. De plus, si $\sigma$ est un cycle, alors cette $p$-chaîne non-singulière étoilée est enveloppante.
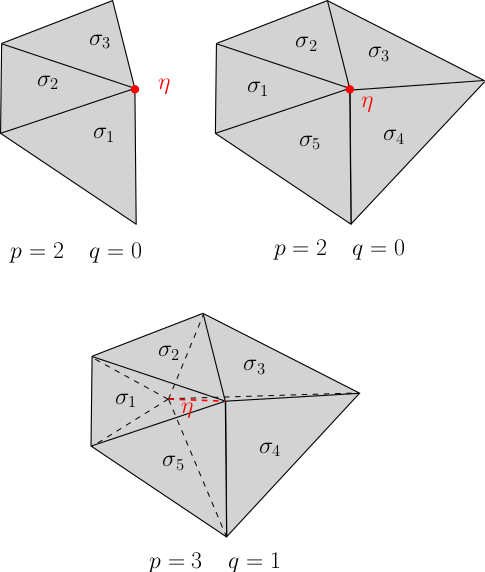
- Des $p$-chaînes étoilées dont le centre est un $q$-simplexe $\eta$ pour différentes valeurs de $p$ et $q$. La première n’est pas enveloppante. La deuxième et la troisième le sont.
Soient $p,q$ deux entiers tels que $0 \leq q \leq p < n$. Soient $\eta$ un $q$-simplexe non-singulier, $\zeta$ une $p$-chaîne non-singulière étoilée de centre $\eta$, et $\xi$ une $(p+1)$-chaîne non-singulière étoilée de centre $\eta$. On dit que $\zeta$ est la base de $\xi$ relativement à $\eta$, si $\eta$ n’est pas une $q$-facette de la $p$-chaîne $\partial_{p+1}\xi-\zeta$.
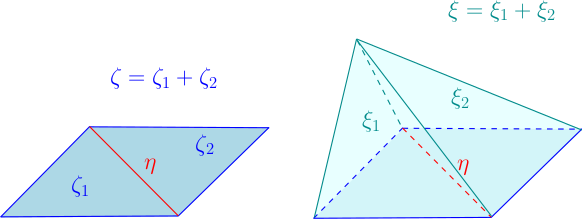
- Un $1$-simplexe $\eta$, une $2$-chaîne étoilée $\zeta$ de centre $\eta$, base d’une $3$-chaîne étoilée $\xi$ de centre $\eta$
Remarquons que cela implique que $\zeta$ est une sous-chaîne du bord de $\xi$. Remarquons aussi qu’une $p$-chaîne non-singulière étoilée qui est la base d’une $(p+1)$-chaîne non-singulière étoilée est nécessairement enveloppante [3]. La propriété « être la base d’une $(p+1)$-chaîne non-singulière étoilée » est une généralisation de la propriété « être la base d’un cône ». En effet, si $\zeta$ est une $p$-chaîne affine non-singulière étoilée de centre $\eta$, et si $x$ est un point de $\mathbb{R}^n$ tel que le cône de sommet $x$ et de base $\zeta$ est constitué de simplexes non-singuliers [4], alors ce cône est une $(p+1)$-chaîne non-singulière étoilée, de centre $\eta$, et de base $\zeta$ relativement à $\eta$. L’avantage de cette généralisation est qu’elle est compatible avec les combinaisons linéaires :
La notion de base est compatible avec les combinaisons linéaires. Si $\zeta_1,\dots,\zeta_\ell$ sont des $p$-chaînes non-singulières étoilées de même centre $\eta$, et si $\xi_1,\dots,\xi_\ell$ sont des $(p+1)$-chaînes non-singulières étoilées de centre $\eta$ et de bases respectives $\zeta_1,\dots,\zeta_\ell$ relativement à $\eta$, alors $\xi_1+\dots+\xi_\ell$ est une $(p+1)$-chaîne non-singulière étoilée de centre $\eta$ et de base $\zeta_1+\dots+\zeta_\ell$ relativement à $\eta$.
Par ailleurs, la propriété « être la base d’une $(p+1)$-chaîne non-singulière étoilée de centre $\eta$ » est une sorte d’analogue pour les $p$-chaînes non-singulières étoilées de centre $\eta$, de la propriété « être le bord d’une $(p+1)$-chaîne non-singulière » pour les $p$-cycles non-singuliers.
On notera aussi que la propriété « être la base d’une $(p+1)$-chaîne relativement à $\eta$ » est d’autant plus difficile à remplir que la dimension de $\eta$ est petite. En effet, considérons une $p$-chaîne non-singulière étoilée $\zeta$ de centre $\eta$, et supposons que $\zeta$ est la base, relativement à $\eta$, d’une $(p+1)$-chaîne non-singulière étoilée $\xi$. Considérons une $r$-facette $\theta$ de $\eta$. Alors $\zeta$ peut aussi être vue comme une $p$-chaîne étoilée de centre $\theta$ et $\xi$ comme une $(p+1)$-chaîne étoilée de centre $\theta$. Mais $\zeta$ vue comme chaîne étoilée de centre $\theta$ n’est pas nécessairement la base de $\xi$ relativement à $\theta$ : il est possible que $\theta$ soit une $r$-facette de la $p$-chaîne $\partial\xi-\zeta$, sans que $\eta$ soit une $q$-facette de $\partial\xi-\zeta$. C’est par exemple le cas sur la figure ci-dessus, si $\theta$ est l’une des extrémités de l’arête $\eta$.
Les notions définies ci-dessus se comportent bien par rapport à l’opérateur de déformation :
Soit $\eta$ un $q$-simplexe non-singulier, $\zeta$ une $p$-chaîne non-singulière étoilée de centre $\eta$, et $\eta'$ un $q$-simplexe non-singulier proche de $\eta$, tous trois à valeurs dans $\mathbb{R}^n$. Alors :
- $\zeta':=\Phi_{\eta}^{\eta'}(\zeta)$ est une $p$-chaîne non-singulière étoilée de centre $\eta'$ ;
- Si $\zeta$ est enveloppante, alors $\zeta'$ l’est aussi ;
- Si $\xi$ est une $(p+1)$-chaîne non-singulière étoilée de centre $\eta$ et si $\zeta$ est la base de $\xi$ relativement à $\eta$, alors $\xi':=\Phi_{\eta}^{\eta'}(\xi)$ est une $(p+1)$-chaîne non-singulière étoilée de centre $\eta'$ et $\zeta'$ est la base de $\xi'$ relativement à $\eta'$.
Démonstration. L’opérateur de déformation des simplexes a été défini de telle sorte que, si $\eta$ est une facette du simplexe $\sigma$, alors $\eta'$ est une facette du simplexe déformé $\Phi_\eta^{\eta'}(\sigma)$. La première assertion en découle immédiatement.
Nous avons vu par ailleurs que l’opérateur de déformation des simplexes commute avec l’opérateur de bord (propriété 1). Ainsi, on a $\partial_p\Phi_\eta^{\eta'}(\zeta)=\Phi_{\eta}^{\eta'}(\partial_p\zeta)$. Si $\zeta$ est enveloppante, alors $\eta$ n’est pas une facette de $\partial_p\zeta$, donc $\eta'$ n’est pas une facette de $\Phi_{\eta}^{\eta'}(\partial_p\zeta)=\partial_p(\Phi_\eta^{\eta'}(\zeta))$, donc $\Phi_\eta^{\eta'}(\zeta)$ est enveloppante. La deuxième assertion est ainsi démontrée.
Si $\xi$ est une $(p+1)$-chaîne non-singulière étoilée de centre $\eta$, la première assertion (déjà démontrée) implique que $\xi':=\Phi_{\eta}^{\eta'}(\xi)$ est une $(p+1)$-chaîne non-singulière étoilée de centre $\eta'$. Si $\zeta$ est la base de $\xi$ relativement $\eta$, alors $\eta$ n’est pas une facette de $\partial_{p+1}\xi-\zeta$. En utilisant la commutation des opérateurs de déformation et de bord, on a
$$\partial_{p+1}\xi'-\zeta' = \partial_{p+1} \Phi_{\eta}^{\eta'}(\xi) - \Phi_{\eta}^{\eta'}(\zeta) = \Phi_{\eta}^{\eta'}(\partial_{p+1}\xi-\zeta).$$
Or $\eta$ n’est pas une facette de $\partial_{p+1}\xi-\zeta$, donc $\eta'$ n’est pas une facette de $\Phi_{\eta}^{\eta'}(\partial_{p+1}\xi-\zeta)$. Par conséquent, $\zeta'$ est une base de $\xi'$ relativement à $\eta'$, et la troisième assertion est démontrée.
C.Q.F.D.
Nous avons déjà dit que la condition est une propriété « être la base d’une $(p+1)$-chaîne reltaivement à $\eta$ » est un analogue pour les $p$-chaînes non-singulières étoilées de centre $\eta$ de la propriété « être le bord d’une $(p+1)$-chaîne non-singulière » pour les $p$-cycles non-singuliers. Si $\omega$ est une $p$-chaîne non-singulière et $\eta$ une $q$-facette de $\omega$, montrer que « l’étoile de $\eta$ dans $\omega$ est la base d’une $(p+1)$-chaîne relativement à $\eta$ » revient en quelque sorte à montrer que « $\omega$ est localement le bord d’une $(p+1)$-chaîne non-singulière au voisinage de $\eta$ ». La proposition suivante est donc une étape importante de la preuve de la Proposition clé :
Pour tout entier $q\in\{0,\dots,p\}$ et tout $q$-simplexe non-singulier $\theta$, toute $p$-chaîne non-singulière étoilée enveloppante de centre $\theta$ est la base, relativement à $\theta$, d’une $(p+1)$-chaîne non-singulière.
Nous allons admettre provisoirement cette proposition, et expliquer comment elle permet de terminer la preuve de la Proposition clé (et donc de la trivialité des groupes d’homologie de l’espace affine).
Fin de la preuve de la Proposition clé en admettant que les $p$-chaînes étoilées sont des bases
Notre Proposition clé repose sur la Proposition ci-dessus, qui affirme que les chaînes étoilées sont des bases, ainsi que sur le lemme important suivant :
Soit $\eta$ un $q$-simplexe non-singulier, $\zeta$ une $p$-chaîne non-singulière étoilée de centre $\eta$, et $\eta'$ un $q$-simplexe non-singulier proche de $\eta$, tous à valeurs dans $\mathbb{R}^n$. On suppose que :
- les $q$-simplexes $\eta$ et $\eta'$ ont le même bord.
- $\zeta$ est la base, relativement à $\eta$, d’une $(p+1)$-chaîne non-singulière étoilée.
Alors la $p$-chaîne non-singulière $\Phi_{\eta}^{\eta'}(\zeta)-\zeta$ est le bord d’une $(p+1)$-chaîne non-singulière.
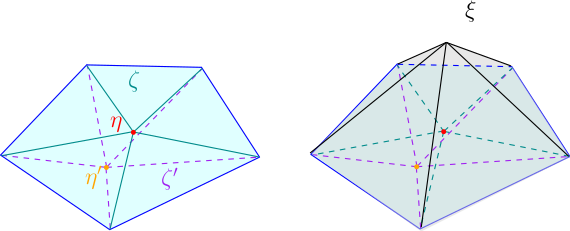
- Ilustration de la preuve : si la $2$-chaîne étoilée $\zeta$ est la base d’une $3$-chaîne étoilée, et si $\zeta’$ est une déformation de $\zeta$, alors $\zeta’-\zeta$ est un bord
Démonstration du lemme important. C’est une conséquence de la commutation de l’opérateur de déformation des simplexes et de l’opérateur de bord (propriété 1). Par hypothèse, $\zeta$ est la base, relativement à $\eta$, d’une $(p+1)$-chaîne non-singulière étoilée $\xi$. Ceci signifie que $\eta$ n’est pas une facette de la $p$-chaîne $\delta:=\partial_{p+1}\xi-\zeta$. D’après la propriété 1, on a
$$\partial_{p+1}\left(\Phi_{\eta}^{\eta'}(\xi)-\xi\right) = \Phi_{\eta}^{\eta'}(\partial_{p+1}\xi)-\partial_{p+1}\xi = \left(\Phi_{\eta}^{\eta'}(\delta)-\delta\right)+\left(\Phi_{\eta}^{\eta'}(\zeta)-\zeta\right).$$
Nous allons montrer que $\Phi_{\eta}^{\eta'}(\delta)=\delta$.
Pour ce faire, considérons maintenant un $p$-simplexe $\tau$ de la $p$-chaîne $\delta$. Alors $\tau$ est une $p$-facette d’un $(p+1)$-simplexe $\kappa$ de la $(p+1)$-chaîne $\xi$. Notons que $\eta$ est une $q$-facette de $\kappa$ (puisque $\xi$ est étoilée de centre $\eta$). Ainsi, $\tau$ et $\eta$ sont deux facettes d’un même simplexe non-singulier $\kappa$. Par conséquent, $\tau$ et $\eta$ :
- soit n’ont pas de facette commune, on a alors immédiatement $\Phi_{\eta}^{\eta'}(\tau)=\tau$ ;
- soit s’intersectent le long d’une $r$-facette commune $\theta$. Dans ce cas, par définition de l’opérateur de déformation des simplexes, on a $\Phi_{\eta}^{\eta'}(\tau)=\Phi_{\theta}^{\theta'}(\tau)$, où $\theta'$ désigne la facette de $\eta'$ correspondant à $\theta$. Mais on remarque que $\theta$ n’est pas égal à $\eta$ tout entier, puisque $\eta$ n’est pas une facette de $\delta$. Et, comme nous avons supposé que les bords des simplexes $\eta$ et $\eta'$ coïncident, on a donc $\theta'=\theta$. Et, par suite, $\Phi_{\eta}^{\eta'}(\tau)=\Phi_{\theta}^{\theta'}(\tau)=\tau$. Comme cette égalité est valable pour chaque $p$-simplexe $\tau$ de $\delta$, on obtient l’égalité $\Phi_{\eta}^{\eta'}(\delta)=\delta$ comme annoncé.
En reprenant l’égalité obtenue au début de la preuve, on en déduit
$$\partial_{p+1}\left(\Phi_{\eta}^{\eta'}(\xi)-\xi\right) = \Phi_{\eta}^{\eta'}(\zeta)-\zeta.$$
Ainsi, la $p$-chaîne $\Phi_{\eta}^{\eta'}(\zeta)-\zeta$ est le bord de la $(p+1)$-chaîne non-singulière $\Phi_{\eta}^{\eta'}(\xi)-\xi$.
CQFD
Démonstration de la Proposition clé. La preuve consiste à déformer $\omega$ vers $\omega'$, en poussant une à une les facettes de $\omega$ vers celles de $\omega'$, par dimension croissante. Notons $\eta_1,\dots,\eta_m$ les facettes du $p$-cycle $\omega$, ordonnées par dimension croissante : $\eta_1$ est un sommet et $\eta_m$ un $p$-simplexe. Notons $\eta_1',\dots,\eta_m'$ les facettes correspondantes dans le $p$-cycle $\omega'$. Nous allons construire par récurrence une suite de $p$-cycles non-singuliers $\omega^0,\dots,\omega^m$, tous proches de $\omega$, et ayant tous les mêmes relations d’incidence que $\omega$. Nous noterons $\eta_j^i$ la facette de $\omega^i$ correspondant à $\eta_j$ (cette définition a bien un sens dès lors que $\omega^i$ sera proche de $\omega$). La suite de $p$-cycles $\omega^0,\dots,\omega^m$ satisfera :
- $\omega^0=\omega$ ;
- pour tout $i\geq 1$, les $i$ premières facettes $\eta_1^i,\dots,\eta_i^i$ de $\omega^i$ coïncident avec les $i$ premières facettes $\eta_1',\dots,\eta_i'$ de $\omega'$ ;
- pour tout $i\geq 1$, $\omega^i-\omega^{i-1}$ est le bord d’une $(p+1)$-chaîne.
La deuxième propriété ci-dessus implique en particulier que $\omega^m=\omega'$. La troisième implique que $\omega^m-\omega^0=\omega'-\omega$ est le bord d’une $(p+1)$-chaîne non-singulière. La construction de cette suite de $p$-cycles conclura donc la preuve de la proposition.
Supposons $\omega^i$ construit. On obtient $\omega^{i+1}$ par déformation de $\omega^i$ en poussant $\eta_{i+1}^{i}$ sur $\eta_{i+1}'$. Autrement dit, on pose
$$\omega^{i+1}:=\Phi_{\eta_{i+1}^i}^{\eta_i'}(\omega^i).$$
Remarquons que $\omega^{i+1}$ est bien défini et est proche de $\omega$, pourvu que $\omega^i$ soit proche de $\omega$. Ceci montre que l’on peut effectivement construire la suite par récurrence. D’autre part, $\omega^{i+1}$ a les mêmes relations d’incidence que $\omega^i$, donc que $\omega$. Vérifions que $\omega^{i+1}$ satisfait les propriétés souhaitées.
Par définition de l’opérateur de déformation, la $(i+1)^{eme}$ facette de $\omega^{i+1}$ est égale à $\eta_{i+1}'$. Par ailleurs, puisque les $i$ premières facettes de $\omega^{i}$ coïncidaient déjà avec des facettes de $\omega'$, elles ne bougent pas quand on pousse $\eta_{i+1}^i$ sur $\eta_{i+1}'$. Par conséquent, les $(i+1)$ premières facettes $\eta_1^i,\dots,\eta_{i+1}^{i+1}$ de $\omega^{i+1}$ coïncident avec les $(i+1)$ premières facettes $\eta_1',\dots,\eta_{i+1}'$ de $\omega'$.
Notons $\zeta_{i+1}$ l’étoile de la facette $\eta_{i+1}^{i}$ dans $\omega^{i}$. Puisqu’on pousse les facettes par dimension croissante, le bord de $\eta_{i+1}^i$ coïncide avec celui de $\eta_i'$. On en déduit que l’opérateur de déformation $\Phi_{\eta_{i+1}^i}^{\eta_i'}$ laisse invariant tous les simplexes qui « ne contiennent pas $\eta_{i+1}^i$ » (c’est-à-dire dont $\eta_{i+1}^i$ n’est pas une facette). On a donc
$$\omega^{i+1}-\omega^i=\Phi_{\eta_{i+1}^i}^{\eta_i'}(\zeta_{i+1})-\zeta_{i+1}.$$
Par définition, $\zeta_{i+1}$ est une $p$-chaîne étoilée de centre $\eta_{i+1}^{i}$. Cette $p$-chaîne étoilée est de plus enveloppante, puisque $\omega$ (et donc aussi $\omega^{i}$) est un cycle. D’après la proposition qui affirme que les les chaînes étoilées sont des bases, $\zeta_{i+1}$ est donc la base, relativement à $\eta_{i+1}^i$, d’une $(p+1)$-chaîne étoilée. Par ailleurs, nous avons déjà remarqué que le bord de la $q$-facette $\eta_{i+1}^i$ coïncide avec le bord de $\eta_{i+1}'$. On peut donc appliquer le lemme important ci-dessus, et en déduire que $\omega^{i+1}-\omega^i=\Phi_{\eta_{i+1}^i}^{\eta_i'}(\zeta_{i+1})-\zeta_{i+1}$ est le bord d’une $(p+1)$-chaîne non-singulière. Le $p$-cycle $\omega^{i+1}$ satisfait donc les propriétés souhaitées.
Ceci termine la preuve de la Proposition clé (et donc de la trivialité des groupes d’homologie de l’espace affine, sous réserve de la Proposition qui affirme que les les chaînes étoilées sont des bases).
CQFD
Les $p$-chaînes étoilées sont des bases
Il nous reste à prouver la Proposition qui affirme que les les chaînes étoilées sont des bases. La preuve se fait par récurrence descendante sur l’entier $q$, c’est-à-dire sur la dimension du centre de la chaîne étoilée considérée. Le cœur de la preuve reprend la même stratégie que celle utilisée ci-dessus pour démontrer la Proposition clé : on déforme la $p$-chaîne étoilée en poussant ses facettes une à une, par dimension croissante [5] Au cours de la preuve, nous aurons besoin de deux lemmes. Le premier est, en quelque sorte, une version faible du Lemme de Whitehead pour les chaînes étoilées. Il s’agit cependant d’un résultat beaucoup plus facile que le lemme de Whitehead, car on s’autorise à bouger le bord de la chaîne étoilée considérée :
Soient $\theta$ un $q$-simplexe non-singulier, et $\zeta$ une $p$-chaîne non-singulière étoilée de centre $\theta$, tous deux à valeurs dans $\mathbb{R}^n$, avec $0\leq q\leq p\leq n$. On suppose que le $q$-simplexe $\theta$ est affine. Alors on peut trouver un chemin continu $(\zeta_t)_{t\in [0,1]}$ de $p$-chaînes non-singulières étoilées de centre $\theta$, tel que :
- $\zeta_0=\zeta$,
- pour tout $t$, la $p$-chaîne $\zeta_t$ a les mêmes relations d’incidence relatives à $\theta$ que $\zeta$,
- les simplexes non-singuliers constituant la $p$-chaîne $\zeta_1$ sont affines.
La démonstration de ce lemme est assez technique, et peut (doit ?) être omise en première lecture.
Considérons un $p$-simplexe non-singulier $\sigma$ admettant $\theta$ comme $q$-facette. Nous allons expliquer comment « redresser » $\sigma$, i.e. comment construire une famille continue $(\sigma_t)_{t\in [0,1]}$ de $p$-simplexes non-singuliers admettant $\theta$ comme facette, joignant $\sigma_0=\sigma$ à un $p$-simplexe non-singulier affine $\sigma_1$.
Notations. Commençons par introduire quelques notations. Par définition, $\sigma$ est un plongement du $p$-simplexe géométrique standard $\Delta=\Delta_p$ dans l’espace affine $\mathbb{R}^n$. Dire que $\theta$ est une $q$-facette, c’est dire que $\theta$ est la composée de la restriction de $\sigma$ à une $q$-facette $\delta$ de $\Delta$ et du paramétrage affine canonique de $\delta$ (qui, rappelons-le, est une bijection affine entre le $q$-simplexe géométrique standard $\Delta_q$ et $\delta$, voir cet article). Par hypothèse, $\theta$ est affine, autrement dit la restriction de $\sigma$ à $\delta$ est affine. On notera $b$ l’isobarycentre de $\delta$. On notera $\bar\delta$ la $(p-q)$-facette de $\Delta$ opposée à $\delta$ (c’est-à-dire l’enveloppe convexe des sommets de $\Delta$ qui ne sont pas des sommets de $\delta$). On notera
$$\pi:\Delta\setminus\bar\delta\to\delta$$
la projection affine de $\Delta$ sur $\delta$ : l’image du point $x$ par $\pi$ est l’intersection de $\delta$ avec l’espace affine engendré par $x$ et $\bar\delta$.
On notera
$$\bar\pi:\Delta\setminus\delta\to\bar\delta$$
la projection affine de $\Delta$ sur $\hat\delta$. Pour tout $x\in(\Delta\setminus(\delta\cup\bar\delta)$, on notera $t(x)$ l’unique réel de $]0,1[$ tel que
$$x=(1-t(x)).\pi(x)+t(x).\bar\pi(x).$$
On peut alors prolonger continûment la fonction $x\mapsto t(x)$ à $\Delta$ tout entier, en posant $t(x)=0$ si $x\in\delta$ et $t(x)=1$ si $x\in\bar\delta$.
Pour $\epsilon>0$, on considérera l’ensemble
$$V_\epsilon:=\{x\in \Delta\mbox{ tel que }t(x)\leq \epsilon\}.$$
C’est un voisinage de $\delta$ dans $\Delta$.
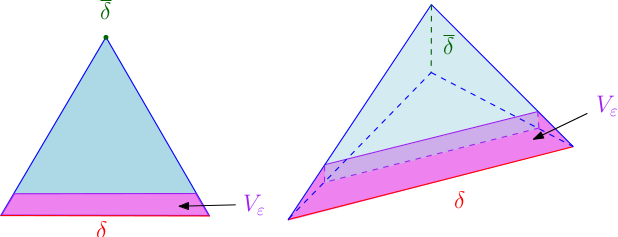
- Le voisinage $V_\epsilon$
Détorsion. Nous allons « détordre $\sigma$ le long de $\delta$ ». Plus précisément, nous allons définir une famille continue de $p$-simplexes singuliers $(\sigma_s')_{s\in [0,1]}$ joignant $\sigma_0'=\sigma$ à un $p$-simplexe $\sigma_1'=\sigma'$ dont la différentielle le long de $\delta$ sera constante.
On considère l’application $\sigma':\Delta_p\to\mathbb{R}^n$ définie par (rappelons que $b$ est l’isobarycentre de $\delta$)
$$\sigma'(x):=\sigma((1-t(x)).b+t(x).\bar\pi(x))+(1-t(x)).(\sigma(\pi(x))-\sigma(b)).$$
C’est un $p$-simplexe singulier, c’est-à-dire une application continue (et même lisse) de $\Delta_p$ dans $\mathbb{R}^n$ ; par contre, ce n’est pas a priori un $p$-simplexe non-singulier (il n’y a aucune raison pour que $\sigma'$ soit injectif). Ce $p$-simplexe singulier ne dépend que de sa restriction au $q$-simplexe géométrique $\delta$ et de sa restriction au $(p-q+1)$-simplexe géométrique $\mathrm{Conv}(b,\bar\delta)$. Le point important (qui découle de la formule ci-dessus, et du fait que $\sigma$ est affine en restriction à $\delta$) est que la différentielle de $\sigma'$ est constante le long de $\delta$ :
Propriété 1. Pour tout $x\in\delta$, on a $d\sigma'(x)=d\sigma(b)$.
Il est bien sûr sous-entendu qu’on identifie les espaces tangent à $\Delta_p$ en $x$ et $b$, ainsi que les espaces tangents à $\mathbb{R}^n$ en $\sigma'(x)$ et $\sigma'(b)$, en utilisant les structures affines de $\Delta_p$ et $\mathbb{R}^n$.
Pour joindre $\sigma$ à $\sigma'$, on considère la famille continue de $p$-simplexes singuliers $(\sigma'_s)_{s\in [0,1]}$ définie par
$$\scriptsize{\sigma'_s(x):=\sigma((1-t(x)).(s.b+(1-s)\pi(x))+t(x).\bar\pi(x))+s.(1-t(x)).(\sigma(\pi(x))-\sigma(b)).}$$
On vérifie immédiatement que $\sigma'_0=\sigma$ et $\sigma'_1=\sigma'$. Par ailleurs, on remarque que, pour tout $s\in [0,1]$ et tout $x\in\delta$, la différentielle de $\sigma'_s$ au point $x$ est égale à la différentielle de $\sigma$ au point $s.b+(1-s).\pi(x)$. En particulier, puisque $\sigma$ est un plongement, la différentielle de $\sigma_s'$ est de rang maximal en tout point de $x\in\delta$. Par un avatar classique du théorème d’inversion locale, il en résulte que
Propriété 2. Il existe $\epsilon'>0$ tel que, pour tout $s\in [0,1]$, le $p$-simplexe $\sigma'_s$ est un plongement en restriction au voisinage $V_{\epsilon'}$ de $\delta$.
Aplatissement. Nous allons maintenant « aplatir » $\sigma'$, c’est-à-dire l’écraser sur son application affine tangente le long de $\delta$. Soit $\sigma'':\Delta\to\mathbb{R}^n$ le $p$-simplexe affine (plongé) défini par
$$\sigma''(x):=\sigma(b)+d\sigma(b).(x-b).$$
D’après la Propriété 1, $\sigma''$ est l’application affine tangente au $p$-simplexe singulier $\sigma'$ en n’importe quel point de $\delta$ (bien sûr, on identifie le $p$-plan affine contenant $\Delta_p$ avec l’espace tangent à $\Delta_p$ en n’importe quel point de $\Delta_p$). Pour joindre $\sigma'$ à $\sigma''$, on considère simplement la famille de $p$-simplexes singuliers $(\sigma''_s)_{s\in [0,1]}$ définie par
$$\sigma''_s:=s.\sigma'' + (1-s).\sigma'.$$
Pour tout $s$, l’application affine tangente à $\sigma''_s$ en chaque point de $\delta$ n’est autre que $\sigma''$ ; en particulier, elle est de rang maximal. On en déduit
Propriété 3. Il existe $\epsilon''>0$ tel que, pour tout $s\in [0,1]$, le $p$-simplexe $\sigma''_s$ est un plongement en restriction au voisinage $V_{\epsilon''}$ de $\delta$.
Rétraction. Il nous reste maintenant à modifier les $p$-simplexes singuliers $\sigma'_s$ et $\sigma''_s$ afin de les transformer en $p$-simplexes non-singuliers. Pour ce faire, nous allons simplement les composer à la source par une bijection affine qui envoie le $p$-simplexe standard $\Delta_p$ dans un voisinage suffisamment petit de la $q$-facette $\delta$, et utiliser les propriétés 2 et 3 ci-dessus.
Pour tout $r\in [0,1]$, on considère l’application affine $\rho_r:\Delta_p\to\Delta_p$ définie par
$$\rho_r(x)=(1-r).\pi(x)+r.(t(x).\pi(x)+(1-t(x)).\bar\pi(x)).$$
Cette application est une bijection sur son image pour $r\in [0,1[$. Par construction, on a
$$t\left(\rho_r(x)\right)=r.(1-t(x))\leq r$$
En particulier, l’application $\rho_r$ envoie le $p$-simplexe standard $\Delta_p$ dans le voisinage $V_{r}$ de la $q$-facette $\delta$.
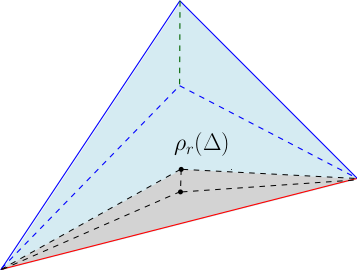
- L’image de la rétraction $\rho_r$
On pose $\epsilon:=\mathrm{min}(\epsilon',\epsilon'')$ où $\epsilon'$ et $\epsilon''$ sont donnés par les Propriétés 2 et 3 ci-dessus. Puis, on définit une famille à un paramètre de $p$-simplexes $(\sigma_t)_{t\in [0,1]}$ comme suit :
- pour $t\in [0,1/3]$, $\sigma_t=\sigma\circ\rho_{(1-3.(1-\epsilon).t)}$,
- pour $t\in [1/3,2/3]$, $\sigma_t=\sigma’_{3t-1}\circ\rho_\epsilon$,
- pour $t\in [2/3,1]$, $\sigma_t=\sigma’'_{3t-2}\circ\rho_\epsilon$. On a bien sûr $\sigma_0=\sigma$. Par ailleurs, $\sigma_1=\sigma''\circ\rho_\epsilon$ est la composée de deux applications affines ; c’est donc un $p$-simplexe affine. On remarque également que $\sigma_t$ coïncide avec $\sigma$ en restriction à $\delta$ pour tout $t$ ; ainsi, $\theta$ est une facette de $\sigma_t$ pour tout $t$. Enfin :
Propriété 4. Pour tout $t\in [0,1]$, $\sigma_t$ est un $p$-simplexe non-singulier.
Cette propriété est clairement vérifiée pour $t\in [0,1/3]$ puisque $\sigma_t$ est alors la composée du $p$-simplexe non-singulier $\sigma$ avec $\rho_{(1-3.(1-\epsilon).t)}$ qui est une application affine injective. Pour $t\in [1/3,1]$, elle découle des Propriétés 2 et 3, et du fait que l’image de $\rho_\epsilon$ est contenue dans la voisinage $V_\epsilon$.
Fin de la preuve du Lemme.
Étant donné un $p$-simplexe non-singulier $\sigma$ admettant $\theta$ comme facette, nous avons donc construit une déformation $(\sigma_t)_{t\in [0,1]}$ joignant continûment $\sigma$ à un $p$-simplexe affine $\sigma_1$, au sein de l’ensemble des $p$-simplexes non-singuliers admettant $\theta$ comme facette. Nous laissons le lecteur vérifier que cette déformation préserve les relations d’incidence relatives à $\theta$. Autrement dit, si $\sigma^1$ et $\sigma^2$ sont deux $p$-simplexes non-singuliers admettant une $r$-facette $\eta$ en commun avec $q\leq r\leq p$, telle que $\theta$ est une $q$-facette de $\eta$, alors les $p$-simplexes déformés $\sigma^1_t$ et $\sigma^2_t$ ont encore une $r$-facette en commun pour tout $t\in [0,1]$.
Soit maintenant $\xi=\sum_i \lambda_i.\sigma^i$ est une $p$-chaîne non-singulière étoilée de centre $\theta$, comme dans l’énoncé du lemme. On considère la famille de $p$-chaînes $(\xi_t)_{t\in [0,1]}$ définie par $\xi_t:=\sum_i\lambda_i.\sigma^i_t$ où $(\sigma^i_t)_{t\in [0,1]}$ est la déformation du $p$-simplexe $\sigma^i$ définie ci-dessus. Il s’agit d’une famille continue de $p$-chaînes non-singulières étoilées de centre $\theta$ avec les même relations d’incidence relatives à $\theta$ que $\xi$, comme souhaité.
CQFD
Le second lemme est une version relative du Lemme important :
Soient $p,q,r$ trois entiers tels que $0\leq r < q < p < n$. Soient $\eta$ un $q$-simplexe non-singulier, $\zeta$ une $p$-chaîne non-singulière étoilée de centre $\eta$, et $\eta'$ un $q$-simplexe non-singulier proche de $\eta$. On suppose que :
- il existe une $r$-facette $\theta$ de $\eta$ qui est encore une facette de $\eta'$,
- $\zeta$ est la base, relativement à $\eta$, d’une $(p+1)$-chaîne non-singulière étoilée.
Alors $\Phi_{\eta}^{\eta'}(\zeta)-\zeta$ est une $p$-chaîne non-singulière étoilée de centre $\theta$, et est de plus la base, relativement à $\theta$, d’une $(p+1)$-chaîne non-singulière étoilée.
Ce lemme est non-trivial et intéressant parce que la dimension de $\theta$ est strictement plus petite que celle de $\eta$. Nous avons expliqué précédemment que la condition « être la base, relativement à $\eta$, d’une $(p+1)$-chaîne non-singulière étoilée » est d’autant plus difficile à satisfaire que la dimension de $\eta$ est petite. Dans l’énoncé du lemme important (version relative), on fait l’hypothèse qu’une $p$-chaîne non-singulière étoilée est la base d’une $(p+1)$-chaîne non-singulière étoilée relativement à $\eta$ (ce qui est une condition relativement facile à satisfaire), et on conclut qu’une autre $p$-chaîne non-singulière étoilée est la base d’une $(p+1)$-chaîne non-singulière étoilée relativement à $\theta$ (ce qui est une condition a priori plus difficile à satisfaire car la dimension de $\theta$ est strictement plus petite que celle de $\eta$).
Démonstration du lemme important (version relative).
Comme $\zeta$ est une $p$-chaîne non-singulière étoilée de centre $\eta$, la $p$-chaîne non-singulière $\zeta':=\Phi_{\eta}^{\eta'}(\zeta)$ est étoilée de centre $\eta'$. L’hypothèse i. implique en particulier que $\theta$ est une $r$-facette commune à $\eta$ et $\eta'$. Par conséquent, $\zeta$ et $\zeta'$ peuvent toutes deux être vues comme des $p$-chaînes non-singulières étoilées de centre $\theta$. Ainsi, $\zeta'-\zeta$ est bien une $p$-chaîne non-singulière étoilée de centre $\theta$.
Pour montrer que $\zeta'-\zeta$ est la base d’une $p$-chaîne non-singulière étoilée de centre $\theta$, on suit la même stratégie que dans la preuve du Lemme important. Par hypothèse, on sait que $\zeta$ est la base d’une $(p+1)$-chaîne étoilée $\xi$, relativement à $\eta$. On considère la $p$-chaîne $\delta:=\partial_{p+1}\xi-\zeta$. On a
$$\partial_{p+1}\left(\Phi_{\eta}^{\eta'}(\xi)-\xi\right) = \Phi_{\eta}^{\eta'}(\partial_{p+1}\xi)-\partial_{p+1}\xi = \left(\Phi_{\eta}^{\eta'}(\delta)-\delta\right)+\left(\Phi_{\eta}^{\eta'}(\zeta)-\zeta\right)$$
Pour conclure la démonstration, il suffit donc de montrer $\theta$ n’est pas une facette de la $p$-chaîne $\Phi_{\eta}^{\eta'}(\delta)-\delta$. Cela découle des mêmes arguments que dans la preuve du Lemme important.
C.Q.F.D.
Démonstration de la proposition « Les chaîne étoilées sont des bases ». La démonstration se fait par récurrence descendante sur l’entier $q$, de $q=p$ à $q=0$.
Pour $q=p$, la proposition est essentiellement triviale. En effet, si $\theta$ est un $p$-simplexe non-singulier, alors toute $p$-chaîne non-singulière étoilée de centre $\theta$ est un multiple $\lambda.\theta$ de $\theta$. Si $\xi$ est un $(p+1)$-simplexe non-singulier dont $\theta$ est l’une des facettes, alors $\lambda.\xi$ une $(p+1)$-chaîne non-singulière étoilée de centre $\theta$ et de base $\lambda.\theta$ relativement à $\theta$. Pour montrer la proposition dans le cas $q=p$, il nous suffit donc de montrer que tout $p$-simplexe non-singulier $\theta$ est une facette d’un $(p+1)$-simplexe non-singulier $\xi$. C’est très facile : dans une carte qui trivialise un voisinage tubulaire de $\theta$, on définit $\xi$ comme étant un cône de base $\theta$.
Fixons maintenant un entier $q_0$, et supposons donc dorénavant la proposition démontrée pour $q=p,p-1,\dots,q_0+1$. Fixons un $q_0$-simplexe non-singulier $\theta$. Nous devons démontrer que toute $p$-chaîne non-singulière étoilée enveloppante de centre $\theta$ est la base d’une $(p+1)$-chaîne non-singulière étoilée relativement à $\theta$. Le point clé est l’affirmation suivante :
Soit $\omega$ une $p$-chaîne non-singulière étoilée enveloppante de centre $\theta$. Si $\omega'$ est une $p$-chaîne non-singulière étoilée de centre $\theta$, suffisamment proche de $\omega$, et ayant les mêmes relations d’incidence que $\omega$, alors $\omega'-\omega$ est la base d’une $(p+1)$-chaîne non-singulière étoilée, relativement à $\theta$.
Cette affirmation doit être vue comme une version relative (au simplexe $\theta$) de la Proposition clé. La stratégie de la preuve est exactement la même que celle de la Proposition clé. Par commodité, on dira qu’une facette $\eta$ de $\omega$ « contient » $\theta$, si $\theta$ est une facette de $\eta$. On considère toutes les facettes de $\omega$, de dimensions comprises entre $q_0+1$ et $p$, « contenant » $\theta$. Notons $\eta_1,\dots,\eta_m$ ces facettes ordonnées par dimension croissantes (ainsi $\eta_1$ est une $(q_0+1)$-facette et $\eta_m$ une $p$-facette). Pour $j\in \{1,\dots,m\}$, on note $\eta_j'$ la facette de $\omega'$ correspondant à $\eta_j$. Comme dans la preuve de la Proposition clé, nous allons construire par récurrence une suite de $p$-chaînes non-singulières étoilées $\omega^0,\dots,\omega^m$ de centre $\theta$, avec les mêmes relations d’incidence que $\omega$, et proches de $\omega$. Pour $i,j\in \{1,\dots,m\}$, on note $\eta_j^i$ l’unique facette de $\omega^i$ proche de $\eta_j$. La suite de $p$-chaînes non-singulières étoilées $\omega^0,\dots,\omega^m$ satisfera $\omega^0=\omega$ et, pour tout $i\in\{1,\dots,m\}$ :
- les $i$ premières facettes $\eta_1^i,\dots,\eta_i^i$ de $\omega^i$ coïncident avec les facettes $\eta_1',\dots,\eta_i'$ de $\omega'$ ;
- la $p$-chaîne non-singulière étoilée $\omega^i-\omega^{i-1}$ est la base d’une $(p+1)$-chaîne non-singulière étoilée de centre $\theta$.
La première propriété ci-dessus implique en particulier que $\omega^m=\omega'$, et la seconde implique que $\omega^m-\omega^0=\omega'-\omega$ est la base d’une $(p+1)$-chaîne non-singulière étoilée relativement à $\theta$. La construction d’une suite de $p$-chaînes non-singulières étoilées satisfaisant ces propriétés conclura donc la preuve de l’affirmation.
Supposons $\omega^i$ construite. On obtient $\omega^{i+1}$ par déformation de $\omega^i$ en poussant la facette $\eta_{i+1}^i$ sur $\eta_{i+1}'$. Autrement dit, on pose
$$\omega^{i+1}:=\Phi_{\eta_{i+1}^i}^{\eta_{i+1}'}(\omega^i).$$
Comme dans la preuve de la Proposition clé, $\omega^{i+1}$ est bien défini et est proche de $\omega$, pourvu que $\omega^i$ soit proche de $\omega$. Ceci montre que l’on peut effectivement construire la suite par récurrence. De plus, $\omega^{i+1}$ a les mêmes relations d’incidence que $\omega^i$, donc que $\omega$. Vérifions que $\omega^{i+1}$ satisfait les propriétés souhaitées.
Par définition de $\omega^{i+1}$, la facette $\eta_{i+1}^{i+1}$ coïncide avec $\eta_{i+1}'$. Par ailleurs, puisque les facettes de $\eta_1^{i},\dots,\eta_{i}^{i}$ de $\omega^i$ coïncidaient déjà avec des facettes de $\omega'$, elles ne bougent pas quand on pousse $\eta_{i+1}^i$ sur $\eta_{i+1}'$ de $\omega'$. Par conséquent, les facettes $\eta_1^{i+1},\dots,\eta_{i+1}^{i+1}$ de $\omega^{i+1}$ coïncident avec les facettes correspondantes de $\omega'$.
Notons $\zeta_{i+1}$ l’étoile de la facette $\eta_{i+1}^{i}$ dans $\omega^{i}$ (c’est-à-dire la somme des simplexes de $\omega^{i}$ qui admettent $\eta_{i+1}^i$ comme facette).
Puisqu’on pousse les facettes « contenant » $\theta$ par dimension croissante, les facettes de $\eta_{i+1}^i$ qui « contiennent » $\theta$ (et sont différentes de $\eta_{i+1}^i$ tout entier) coïncident avec les facettes correspondantes de $\eta_i'$. On en déduit que l’opérateur de déformation $\Phi_{\eta_{i+1}^i}^{\eta_i'}$ laisse invariant tous les $p$-simplexes de $\omega^i$ qui « contiennent » $\theta$, mais ne contiennent pas $\eta_{i+1}^i$. Puisque $\omega^i$ est une chaîne non-singulière étoilée de centre $\theta$, tous les $p$-simplexes de $\omega^i$ contiennent $\theta$. Ainsi l’opérateur de déformation $\Phi_{\eta_{i+1}^i}^{\eta_i'}$ laisse invariant tous les $p$-simplexes de $\omega^i$ qui ne sont pas dans l’étoile $\zeta_{i+1}$ de $\eta_{i+1}^{i}$. On a donc
$$\omega^{i+1}-\omega^i=\Phi_{\eta_{i+1}^i}^{\eta_i'}(\zeta_{i+1})-\zeta_{i+1}.$$
Par définition, $\zeta_{i+1}$ est une $p$-chaîne non-singulière étoilée de centre $\eta_{i+1}^{i}$. Cette $p$-chaîne non-singulière étoilée est enveloppante : en effet, si $\eta_{i+1}^i$ était une facette du bord de $\zeta_{i+1}$, alors ce serait aussi une facette du bord de $\omega^i$ (car $\zeta_{i+1}$ est l’étoile de $\eta_{i+1}^{i}$ dans $\omega^i$), donc $\theta$ serait a fortiori une facette du bord de $\omega^i$, et donc aussi du bord de $\omega$ (par commutation des opérateurs de déformation avec l’opérateur bord), ce qui n’est pas la cas puisque $\omega$ est une chaîne étoilée de centre $\theta$ enveloppante. Comme $r=\mathrm{dim}(\eta_{i+1}^i)=\mathrm{dim}(\eta_{i+1})\geq q_0+1$, notre hypothèse de récurrence affirme que $\zeta_{i+1}$ est la base d’une $(p+1)$-chaîne non-singulière étoilée, relativement à $\eta_{i+1}^{i}$. Par ailleurs, nous avons déjà dit que les facettes de $\eta_{i+1}^i$ (différentes du simplexe $\eta_{i+1}^i$ lui-même) « contenant » $\theta$ coïncident avec celles de $\eta_i'$. On peut donc appliquer le Lemme important (version relative), et en déduire que $\omega^{i+1}-\omega^i=\Phi_{\eta_{i+1}^i}^{\eta_i'}(\zeta_{i+1})-\zeta_{i+1}$ est la base d’une $(p+1)$-chaîne non-singulière. Par conséquent, $\omega^{i+1}$ vérifie les propriétés annoncées, et l’affirmation est démontrée.
Terminons la preuve de la Proposition. Considérons une $p$-chaîne non-singulière étoilée $\zeta$ de centre $\theta$. D’après le lemme de linéarisation des $p$-chaînes non-singulières étoilées, il existe un chemin continu $(\zeta_t)_{t\in [0,1]}$ parmi les $p$-chaînes non-singulières étoilées de centre $\theta$ ayant les mêmes relations d’incidence que $\zeta$, qui part de $\zeta_0=\zeta$ et aboutit en une $p$-chaîne non-singulière étoilée $\zeta_1$ affine dans une certaine carte. D’après l’affirmation, pour tout $t\in [0,1]$, il existe $\epsilon>0$ tel que $\zeta_t-\zeta_{t+\epsilon}$ est la base d’une $(p+1)$-chaîne non-singulière étoilée de centre $\omega$. Par compacité de $[0,1]$, et d’après la Remarque sur les bases de $p$-chaînes étoilées, on en déduit que $\zeta_1-\zeta_0$ est la base d’une $(p+1)$-chaîne non-singulière étoilée de centre $\omega$. Mais, par ailleurs, comme dans la preuve du Lemme sur les cycles affines, le cône affine (dans la carte où $\zeta_1$ est affine) de base $\zeta_1$ et de sommet un point générique est une $(p+1)$-chaîne non-singulière étoilée de centre $\theta$, et de base $\zeta_1$ relativement à $\theta$. Par conséquent (en utilisant à nouveau la Remarque sur les bases de $p$-chaînes étoilées), $\zeta_0$ est la base d’une $(p+1)$-chaîne non-singulière étoilée, relativement à $\theta$. Ceci termine la preuve de la Proposition, et donc aussi de la Proposition clé, et par suite de la trivialité des groupes d’homologie de l’espace affine.
C.Q.F.D.
[1] Rappelons qu’il s’agit d’une bijection affine privilégiée, entre le $q$-simplexe géométrique standard $\Delta_q$ et le $q$-simplexe géométrique affine $\delta$. Voir ici.
[2] Cette terminologie fait bien sûr référence à la notion plus classique d’étoile d’un simplexe. Rappelons que, si $\omega$ est une $p$-chaîne, et si $\eta$ est un $q$-simplexe, alors l’étoile de $\eta$ dans $\omega$ est la somme des $p$-simplexes de $\omega$ admettant $\eta$ comme $q$-facette.
[3] Remarquer que si $\eta$ n’est pas une $q$-facette de la $p$-chaîne $\partial_{p+1}\xi-\zeta$, alors $\eta$ n’est pas non plus une $q$-facette de la $p-1$-chaîne $\partial_p\partial_{p+1}\xi-\partial_p\zeta = -\partial_p\zeta$.
[4] Pour ce faire, il faut et il suffit que $x$ ne soit pas dans l’union des $p$-plans engendrés par les images des simplexes constituant $\zeta$
[5] À tel point que l’on aurait pu, à la suite de Cerf, faire apparaître la Proposition clé comme un cas particulier de la Proposition qui affirme que les les chaînes étoilées sont des bases, en remarquant que tout $p$-cycle admet une subdivision qui peut être considérée formellement comme une $p$-chaîne étoilée de centre vide. Cette astuce formelle nous a semblé peu intuitive, et nous avons préféré ne pas y avoir recours, quitte à rallonger un peu la preuve.
