Revêtements

On rappelle ici les notions de théorie des revêtements nécessaires pour la présentation du groupe fondamental par les lacets. Vous pouvez également consulter cet article sur le même sujet.

Tous les espaces topologiques considérés ici sont raisonnables, c’est à dire des variétés ou des CW-complexes.

On dit que $p : Y \to X$ est un revêtement si $p$ est surjectif et que tout point $x \in X$ possède un voisinage ouvert $U \subset X$ dont l’image réciproque $p^{-1}(U)$ est la réunion disjointe d’une collection d’ouverts $(V_i)_{i\in I}$ de $Y$, tels que la restriction de $p$ à chaque $V_i$ soit un homéomorphisme. Un ouvert $U$ possédant cette propriété est appelé ouvert trivialisant (du revêtement $p$).

On représente souvent l’image réciproque d’un ouvert trivialisant de la façon suivante. En référence à cette image, on dit parfois que les ouverts $(V_i)_{i\in I}$ forment une pile d’assietttes au dessus de $U$.

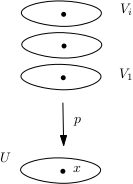
L’image réciproque d’un point $x$ par la projection $p$ est appelée la fibre de $p$ au-dessus $x$. On la notera parfois $F_x$.

Commençons par quelques propriétés des revêtements.

• Les ouverts $V_i$ étant disjoints, la fibre $F_x \subset Y$ est un espace discret.
• L’application qui à un point $x$ associe le cardinal de la fibre $F_x$ de $x$ est localement constante. En particulier, si $X$ est connexe, le cardinal d’une fibre est constant. C’est le degré du revêtement. Si celui-ci est un nombre entier $n$, on dit aussi que $p$ est un revêtement à $n$ feuillets.
• Si $p :Y\to X$ est un revêtement et si $X$ est connexe alors la restriction de $p$ à toute composante connexe de $Y$ est encore un revêtement.
• Un revêtement d’un CW-complexe ou d’une variété est encore un CW complexe ou une variété.

Un revêtement $p : Y \to X$ est dit connexe si $Y$ est connexe. Remarquons que cela entraîne la connexité de $X$.

Pour plus de commodité on appellera revêtement pointé $p : (Y, y_0) \to (X, x_0)$ la donnée d’un revêtement $p : Y \to X$ et de deux points-base $x_0 \in X$, $y_0 \in Y$ tels que $p(y_0) = x_0$.

Revêtements et action de groupe

Les actions de groupes sur les variétés fournissent des exemples naturels de revêtements.

Soit $\Gamma$ un groupe agissant continûment sur $Y$. On dit que l’action de $\Gamma$ sur $Y$ est topologiquement libre (on dit aussi libre et proprement discontinue) si tout point $y \in Y$ admet un voisinage $U$ tel que dont les images par les éléments de $\Gamma$ sont deux à deux disjointes :

$$( g_1\cdot U) \cap ( g_2\cdot U) = \emptyset\mbox{ si } g_1\neq g_2.$$

La proposition suivante est alors quasiment immédiate ; nous la laissons en exercice :

Notons que, dans la situation de la proposition, la fibre $F_{p(y)}$ du point $p(y)$ n’est rien d’autre que l’orbite $\Gamma\cdot y$ de $y$.

Nous avons maintenant de nombreux exemples de revêtements à notre disposition.

• L’action de $\mathbb Z^n$ sur $\mathbb R^n$ par translation est topologiquement libre. On obtient ainsi un revêtement du tore $\mathbb T^n = \mathbb Z^n \backslash \mathbb R^n = \left( \mathbb Z \backslash \mathbb R \right)^n = (S^1)^n$

  $$\begin{array}{cccc} p:&\mathbb R^n &\longrightarrow &\mathbb T^n\\ &(x_i)_{i=1}^n&\longmapsto& ([x_i]_1)_{i=1}^n. \end{array}$$

• L’involution $x \mapsto -x$ définie sur la sphère unité $S^n \subset \mathbb R^{n+1}$ définit une action topologiquement libre du groupe cyclique $\mathbb Z/2\mathbb Z$ dont le quotient s’identifie à l’espace projectif $\mathbb R P^n$, c’est-à-dire à l’ensemble des droites vectorielles de $\mathbb R^{n+1}$. L’application $S^n \to \mathbb R P^n$ est donc un revêtement à deux feuillets.
• Le bouquet de $n$ cercles est le quotient d’un arbre $2n$-valent régulier par le groupe libre $L_n$.

Si $\Gamma$ est un groupe d’action topologiquement libre sur $Y$ et si $\Lambda$ est un sous-groupe de $\Gamma$, tout se passe bien et l’application

$$\begin{array}{cccc} p:& \Lambda\backslash Y&\longrightarrow &\Gamma\backslash Y\\ &\Lambda\cdot y&\longmapsto& \Gamma\cdot y \end{array}$$

est un revêtement dont la fibre s’identifie aux orbites de $\Gamma$ sous l’action de $\Lambda$ par multiplication à gauche.
On obtient le diagramme suivant

$$ \xymatrix{ Y \ar[dr] \ar[r]& \Lambda\backslash Y \ar[d] \\ & \Gamma\backslash Y }$$

Morphismes de revêtements

Soit $p : Y \to X$ et $p' : Y \to X$ deux revêtements de $X$. Un morphisme (de revêtements) est la donnée d’une application continue $f : Y \to Y'$ telle que $p' \circ f = p$.

$$ \xymatrix{ Y \ar[dr]_{p} \ar[rr]^f&& Y' \ar[dl]^{p'} \\ & X & }$$

Soit $p : (Y, y_0) \to (X, x)$ et $p' : (Y', y'_0) \to (X, x)$ deux revêtements pointés de $(X, x)$. Un morphisme (de revêtements pointés) est la donnée d’une application continue $f : Y \to Y'$ telle que $p' \circ f = p$ et $f(y_0) = y'_0$.
Lorsque $f$ est un homéomorphisme, on parle d’isomorphisme de revêtements.

On note $\mathrm{Aut}(p)$ les groupe des automorphismes du revêtement $p$. L’étude de ce groupe est intimement liée à l’étude du groupe fondamental. Lorsque $p :Y\to X$ est le « plus grand » revêtement connexe de $X$ (on parle alors de revêtement universel), le groupe fondamental de $X$ s’identifie à $\mathrm{Aut}(p)$. Cette propriété est le point de départ de la définition de groupe fondamental par les revêtements

Les éléments de $\mathrm{Aut}(p)$ ont des propriétés très particulières.

Démonstration

Considérons un automorphisme $f:Y\to Y$ du revêtement $p$, et supposons que cet automorphisme fixe un point de $Y$. Soit $A$ l’ensemble des points de $y$ qui sont fixés par $f$. Par hypothèse, $A$ n’est pas vide. Par ailleurs, $A$ est fermé car $f$ est continue. Enfin, $A$ est ouvert. En effet, si $y$ est un point de $A$, on peut trouver un ouvert trivialisant $U$ contenant le point $p(y)$, et noter $V$ la composante connexe de $p^{-1}(U)$ contenant $y$. Alors $p:V\to U$ est un homéomorphisme. Comme $p\circ f=p$, et comme $f$ fixe un point de $V$, on en déduit que $f_{\vert V}=\mathrm{Id}$. Ainsi $V\subset A$, ce qui montre que $A$ est ouvert.

Nous avons montré que l’ensemble $A$ est ouvert, fermé et non-vide ; il est donc égal à $Y$ tout entier. Autrement dit, $f$ fixe tous les points $Y$ : c’est l’identité !

C.Q.F.D.

Il existe également une définition plus générale de morphisme de revêtements lorsque les revêtements n’ont pas la même base.