Groupe fondamental d’un quotient

Bien souvent, un espace $X$ apparait naturellement comme le quotient d’un espace topologiquement très simple ($\mathbb{R}^d$, le disque $\mathbb{D}^2$,..) par l’action d’un groupe $\Gamma$. On pensera par exemple au tore $\mathbb{T}^d$ qui apparait comme le quotient de $\mathbb{R}^d$ par son sous-groupe $\mathbb{Z}^d$, ou bien aux surfaces de Riemann qui peuvent presque toutes êtres décrites comme des quotient du disque de Poincaré par un sous-groupe discret de $\mathrm{PSL}(2,\mathbb{R})$ agissant par isométries hyperboliques,... Nous allons maintenant démontrer que le groupe fondamental d’un tel espace $X$ n’est autre que le groupe $\Gamma$. Ce fait, évident quand on construit le groupe fondamental « par les revêtements », ne l’est nullement quand on définit --- comme nous le faisons ici --- le groupe fondamental « par les lacets ».

Rappelons que nous qualifions de $1$-connexe un espace connexe par arcs dans lequel tout lacet est homotope à un lacet constant. Nous allons montrer que le groupe fondamental du quotient d’un espace $1$-connexe sous l’action topologiquement libre d’un groupe $\Gamma$ s’identifie à $\Gamma$.

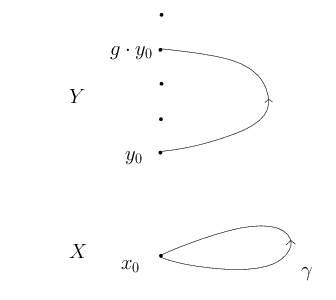
Démonstration. Soit $p : Y \to X$ la surjection canonique (dont on a vu ici qu’elle était un revêtement). On choisit un point-base $y_0 \in Y$ et son image $x_0 = p(y_0) \in X$. On définit alors l’application

$$ \widetilde{\phi} : \Omega(X, x_0) \to \Gamma$$

de la façon suivante : si $\gamma$ est un lacet tracé sur $X$, basé en $x_0$, il existe un unique relevé $\widetilde{\gamma} : I \to Y$ issu de $y_0$ par le théorème de relèvement des homotopies.

Par construction, l’extrémité $\widetilde{\gamma}(1)$ de ce relevé appartient à la fibre de $\gamma(1) = x_0$. Il s’écrit donc $g\cdot y_0$, pour un certain élément $g \in \Gamma$. Comme l’action de $\Gamma$ sur $Y$ est libre, cet élément $g$ est bien déterminé par $\gamma$, ce qui permet de poser $\widetilde{\phi}(\gamma) = g$.

L’élément $\widetilde{\phi}(\gamma)$ ne dépend en fait que de la classe d’homotopie de $\gamma$ par le théorème de relèvement des homotopies. On obtient donc une application

$$ \phi : \pi_1(X,x_0) \to \Gamma.$$

C’est un morphisme, en effet

• $\phi(c_{x_0})=e$ car $\widetilde{c}_{x_0}=c_{y_0}$ ;
• Soit $[\gamma]\in\pi_1(X,x_0)$, on note $\widetilde{\gamma}$ le relevé de $\gamma$ issu de $y_0$ et $g=\phi([\gamma])$. Le chemin $t\mapsto g^{-1}\cdot\widetilde{\gamma}(1-t)$ de $Y$ est issu de $y_0$ et se projette sur $\overline{\gamma}$. Par conséquent, $\phi([\gamma]^{-1})=\phi([\overline{\gamma}])=g^{-1}$ ;
• Soit $[\gamma_1]$ et $[\gamma_2]$ deux éléments de $\pi_1(X,x_0)$. On note $\widetilde{\gamma}_1$ et $\widetilde{\gamma}_2$ leurs relevés issus de $y_0$. Le chemin $\widetilde{\gamma}_1*(\phi([\gamma_1])\cdot\widetilde{\gamma}_2)$ est un relevé de $\gamma_1*\gamma_2$ issu de $y_0$. Par conséquent, $\phi([\gamma_1*\gamma_2])=\phi([\gamma_1])\cdot\phi([\gamma_2])$. L’application $\phi$ est surjective car $Y$ est connexe par arcs et injective car tout lacet de $X$ qui se relève en un lacet de $Y$ est contractile par $1$-connexité de $Y$.

C.Q.F.D.

L’application directe du théorème ci-dessus permet de déterminer les groupes fondamentaux de nombreux espaces usuels.