|
> Groupe fondamental > Groupe fondamental par les lacets > Définition du groupe fondamental "par les lacets" Définition du groupe fondamental "par les lacets" |
La présentation du groupe fondamental à l’aide des lacets commence ici.
La définition du groupe fondamental à l’aide des lacets est déjà présente dans l’Analysis Situs même si Poincaré ne dispose pas de la définition formelle d’homotopie (ce qui lui complique un peu la tâche). Les aspects historiques sont développés ici. L’idée est de comprendre la forme générale d’un espace topologique à partir des courbes tracées cet espace et considérées à déformation près. Cette partie comprend la définition et les premières propriétés du groupe fondamental. En particulier, on montre que le groupe fondamental se comporte bien vis-à-vis des fonctions continues
Dans toute cette partie $X$, $Y$ et $Z$ sont des espaces topologiques jolis c’est à dire des variétés ou des CW-complexes et $I$ représente l’intervalle $[0,1]$.
Définitions
Commençons par préciser les notions de lacet tracé sur un espace et de déformation. Comme on travaille avec des espaces topologiques, on ne considère que des applications continues.
Un chemin dans $X$ est une application continue $\gamma : I\to X$. Un lacet de point base $x\in X$ un chemin $\gamma$ tel que $\gamma(0)=\gamma(1)=x$. On note $\Omega(X,x)$ l’ensemble des lacets de $X$ basés en $x$.
Soient $\gamma_0$ et $\gamma_1$ deux chemins tels que $\gamma_0(1)=\gamma_1(0)$. La concaténation $\gamma_0 *\gamma_1$ de $\gamma_0$ et $\gamma_1$ est le chemin défini par
$$ \gamma_0 *\gamma_1(t)= \left\{ \begin{array}{ll} \gamma_0(2t) &\text{ si } t\in\left[0,\frac{1}{2}\right]\\ \gamma_1(2t-1) &\text{ si } t\in\left[\frac{1}{2},1\right]. \end{array} \right. $$
Ce chemin relie $\gamma_0(0)$ à $\gamma_1(1)$ en parcourant $\gamma_0$ puis $\gamma_1$. Deux lacets ayant le même point base peuvent toujours être concaténés.
Si $\gamma$ est un chemin, on note $\overline\gamma$ le chemin parcouru en sens inverse, c’est à dire le chemin $t\mapsto \gamma(1-t)$. Enfin, on note $c_{x}$ le lacet constant de point base $x$.
Les animations suivantes présentent les chemins $\gamma_0 *\gamma_1$ et $\overline\gamma$ en montrant l’évolution du paramètre.
On considère la relation d’homotopie à extrémités fixées sur l’espace des chemins. Deux chemins $\gamma_0,\gamma_1$ ayant les mêmes extrémités sont dits homotopes (à extrémités fixées) s’il existe une application $H:I^2\to X$ telle que :
- $H(0,t)=\gamma_0(t)$ et $H(1,t)=\gamma_1(t)$ pour tout $t$,
- $H(s,0)=\gamma_0(0)=\gamma_1(0)$ et $H(s,1)=\gamma_0(1)=\gamma_1(1)$ pour tout $s$. En posant
$$\gamma_s(t):=H(s,t),$$
on peut penser à $H$ comme à une famille continues $(\gamma_s)_{s\in I}$ de chemins ayant les mêmes extrémités que $\gamma_0$ et $\gamma_1$. On retiendra donc que $\gamma_0$ et $\gamma_1$ sont homotopes (à extrémités fixées) si on peut passer de l’un à l’autre par une famille continue $(\gamma_s)_{s\in I}$ de chemins dans $X$ ayant les mêmes extrémités.
Les opérations définies ci-dessus sont compatibles avec les homotopies :
- Si $\gamma_0$, $\gamma_1$ et $\gamma_2$ sont trois chemins tels que $\gamma_0(1)=\gamma_1(0)$ et $\gamma_2(0)=\gamma_1(1)$ alors les chemins $(\gamma_0*\gamma_1)*\gamma_2$ et $\gamma_0*(\gamma_1*\gamma_2)$ sont homotopes.
- Si les chemins $\gamma_0$ et $\gamma_1$ et les chemins $\delta_0$ et $\delta_1$ sont homotopes et vérifient $\gamma_0(1)=\delta_0(0)$ (et donc $\gamma_1(1)=\delta_1(0)$) alors les chemins $\gamma_0*\delta_0$ et $\gamma_1*\delta_1$ sont homotopes.
- Pour tout chemin $\gamma$, le lacet $\gamma*\overline\gamma$ est homotope au lacet constant $c_{\gamma(0)}$.
- Pour tout chemin $\gamma$, les chemins $c_{\gamma(0)}*\gamma$ et $\gamma*c_{\gamma(1)}$ sont homotopes à $\gamma$.
La preuve est présentée sous forme d’animations.
La relation d’homotopie à extrémités fixées se restreint à l’ensemble des lacets basés en un point donné. Deux lacets $\gamma_0,\gamma_1$ basés en un même point $x$ sont homotopes (à extrémité fixée) si on peut passer de l’un à l’autre par une famille continue $(\gamma_s)_{s\in I}$ de lacets basés en $x$.
Soit $x\in X$. On note respectivement $\pi_1(X,x)$ l’ensemble $\Omega(X,x)$ quotienté par la relation d’équivalence induite par l’homotopie, et $[\gamma]$ la classe d’équivalence du lacet $\gamma$ dans $\pi_1(X,x)$. L’ensemble $\pi_1(X,x)$ est alors muni d’une structure de groupe dont le produit est donné par la concaténation, l’élément neutre par $[c_{x}]$ et l’inverse de $[\gamma]$ par $[\gamma]^{-1}=[\overline\gamma]$.
Le groupe $\pi_1(X,x)$ est appelé groupe fondamental de $X$ en $x$.
- Pour tout $n\geq 1$, $\pi_1(\mathbb R^n,0)=\{0\}$. En effet si $\gamma$ est un lacet de $\mathbb R^n$ basé en $0$ alors
$$\begin{array}{cccc} H :& I\times I&\longrightarrow &\mathbb R^n\\ &(s,t)&\longmapsto&(1-s)\gamma(t) \end{array} $$
est une homotopie reliant $\gamma$ à $c_0$. Donc tout lacet est homotope au lacet constant.
- Plus généralement, si $A\subset \mathbb R^n$ est étoilé par rapport à l’origine alors $\pi_1(A,0)=\{0\}$.
- On verra plus loin que le groupe fondamental du cercle est $\mathbb Z$. L’élément de $\mathbb Z$ associé à un lacet compte le nombre de tours que fait ce lacet autour de l’origine. On peut trouver ici une preuve du théorème de la boule chevelue en dimension $2$ utilisant le groupe fondamental du cercle
Le calcul de groupes fondamentaux non triviaux (comme celui du cercle) n’est pas immédiat avec cette définition. Une façon naturelle d’aborder cette question est d’utiliser les théorèmes de relèvement des chemins et des homotopies. Ces théorèmes permettent de traiter une large classe d’exemples obtenus par quotient d’un espace topologique sous l’action continue d’un groupe discret. Nous reportons donc l’étude du groupe fondamental du cercle, toutefois le lecteur pressé peut consulter [1] pour une preuve qui redémontre les propriétés de relèvement dans ce cas particulier ou [2] pour une preuve utilisant la théorie du degré.
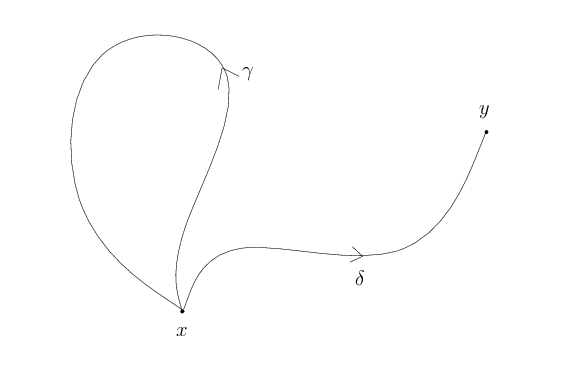
Le groupe fondamental dépend donc du choix d’un point base pour les lacets. Nous allons maintenant voir ce qui se passe si on change ce point base. On suppose que $X$ est connexe par arcs. Soit $x$ et $y$ deux points de $X$ et $\delta$ un chemin reliant $x$ à $y$.
$$ \begin{array}{cccc} \psi_\delta:& \pi_1(X,x)&\longrightarrow &\pi_1(X,y)\\ &[\gamma]&\longmapsto&[\overline{\delta}*\gamma*\delta] \end{array} $$
est un isomorphisme.
Par définition de la concaténation $\psi_\delta$ est un morphisme de groupe. De plus, l’application
$$ \begin{array}{cccc} \psi_{\overline{\delta}}:& \pi_1(X,y)&\longrightarrow &\pi_1(X,x)\\ &[\gamma]&\longmapsto&[\delta*\gamma*[\overline{\delta}] \end{array} $$
est aussi un morphisme de groupe et vérifie $\psi_\delta\circ\psi_{\overline{\delta}}=\mathrm{Id}$ et $\psi_{\overline{\delta}}\circ\psi_\delta=\mathrm{Id}$.
Donc $\psi_\delta$ est un isomorphisme d’inverse $\psi_{\overline{\delta}}$.
Si $X$ est connexe par arcs, le groupe fondamental ne dépend donc pas du choix de point base, on le notera parfois un peu abusivement $\pi_1(X)$.
On dit qu’un espace connexe par arcs est $1$-connexe si son groupe fondamental est trivial, c’est-à-dire si tout lacet de cet epsace est homotope à un lacet constant.
L’espace $\mathbb R^n$ est $1$-connexe.
La terminologie $1$-connexe est peu fréquente ; la plupart des auteurs préfèrent utiliser le syntagme simplement connexe. Nous profitons de ces deux termes pour distinguer (provisoirement) nos deux approches du groupes fondamental :
- nous qualifions de $1$-connexe un espace dans lequel tout lacet est homotope à un lacet constant (c’est-à-dire un espace dont le groupe fondamental « au sens des lacets » est trivial) ;
- nous qualifiions de simplement connexe un espace qui ne possède aucun revêtement connexe non-trivial (voir plus loin) (c’est-à-dire un espace dont le groupe fondamental « au sens des revêtements » est trivial) . Nous montrerons plus tard que ces deux notions coïncident.
Nous allons maintenant voir comment certaines opérations usuelles sur les espaces topologiques transforment le groupe fondamental.
Morphismes induits
Soit $x\in X$ et $f :X\to Y$ une application continue. On définit l’application
$$ \begin{array}{cccc} f_*:& \pi_1(X,x)&\longrightarrow &\pi_1(Y,f(x))\\ &[\gamma]&\longmapsto&[f\circ\gamma] \end{array} $$
L’application $f_*$ est un morphisme de groupes car pour tous lacets $\gamma_0$ et $\gamma_1$, on a $f(\gamma_0*\gamma_1)=f(\gamma_0)*f(\gamma_1)$. Si $f : X\to Y$ et $g : Y\to Z$ sont des applications continues alors $(g\circ f)_*=g_*\circ f_*$ par définition.
Le groupe fondamental est donc invariant par homéomorphisme. On verra un peu plus loin que c’est un invariant bien plus général. Cette invariance permet de montrer que des espaces topologiques ne sont pas homéomorphes.
Groupe fondamental, catégories et foncteurs
En un sens, l’objet de la topologie algébrique est la définition et l’étude de foncteurs entre la catégorie des espaces topologiques et celle des groupes. Ainsi les propriétés des morphismes induits se reformulent de façon plus algébrique en le groupe fondamental définit un foncteur de la catégorie des espaces topologiques pointés dans la catégorie des groupes. L’homologie est un autre exemple fondamental de tel foncteur. Plus formellement, notre foncteur $F : \mathrm{Top}\to \mathrm{Gps}$ est défini par
$$F((X,x_0))=\pi_1(X,x_0)$$
et
$$F(f : (X,x_0)\to(Y,y_0))=f_* :\pi_1(X,x_0)\to \pi_1(Y,y_0).$$
Groupe fondamental d’un produit
Soit $x\in X$ et $y\in Y$. On note $p$ et $q$ les projections de $X\times Y$ sur $X$ et $Y$.
L’application \[(p_*,q_*) : \pi_1(X\times Y, (x,y))\to \pi_1(X,x)\times \pi_1 (Y,y)\] est un isomorphisme.
L’application $\phi=(p_*,q_*)$ est un morphisme de groupes.
Il est injectif car si $\phi([\gamma,\delta])=0$, il existe des homotopies $(\gamma_s)_{s\in[0,1]}$ et $(\delta_s)_{s\in[0,1]}$ reliant $\gamma$ et $\delta$ aux lacets constants $c_x$ et $c_y$. Donc $(\gamma_s,\delta_s)_{s\in[0,1]}$ est une homotopie reliant $(\gamma,\delta)$ au lacet constant $(c_x,c_y)$.
Il est surjectif car $\phi([(\gamma,\delta)])=([\gamma],[\delta])$ pour tous
$(\gamma,\delta)\in\Omega(X,x)\times \Omega(Y,y)$.
Donc $\phi$ est un isomorphisme..
C.Q.F.D
- Le groupe fondamental du tore de dimension $n$, $T^n=S^1\times\dots\times S^1$ est $\mathbb Z^n$.
- Le groupe fondamental du tore plein $D^2\times S^1$ est $\mathbb Z$.
Homotopie et groupe fondamental
Nous avons vu que le groupe fondamental se comporte bien sous l’action des fonctions continues. Nous allons voir que l’effet d’une fonction continue ne dépend que de sa classe d’homotopie.
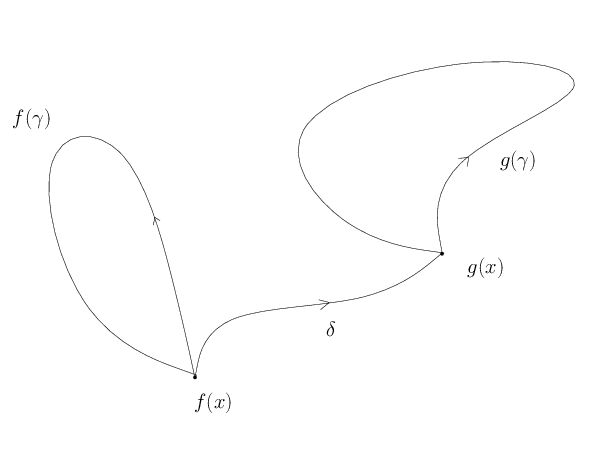
Soit $f:X\to Y$ et $g:X\to Y$ deux applications homotopes et $x\in X$. On note $H$ une homotopie entre $f$ et $g$ et $\delta=H(\cdot,x)$.
Alors
$$g_*=\psi_\delta\circ f_*$$
où $\psi_\delta :\pi_1(Y,f(x))\to\pi_1(Y,g(x))$ est donné ici.
En particulier, si $f$ et $g$ sont homotopes relativement à $x$ alors $f_*=g_*$.
Soit $\gamma$ un lacet de $X$ de point base $x$. On veut montrer que $f(\gamma)$ et $\delta*g(\gamma)*\overline{\delta}$ sont homotopes.
Pour tout $s\in[0,1]$, on pose
$$ \begin{array}{cccc} \delta_s:& [0,1]&\longrightarrow &Y\\ &t&\longmapsto& H(st,x). \end{array} $$
Le chemin $\delta_s$ est un chemin de $Y$ reliant $f(x)$ à $H(s,x)$. En particulier, $\delta_0$ est le lacet constant en $f(x)$ et $\delta_1=\delta$. L’homotopie
$$ \begin{array}{cccc} & [0,1]\times [0,1]&\longrightarrow &Y\\ &(s,t)&\longmapsto& \delta_s*H(s,\gamma(t))*\overline{\delta_s} \end{array} $$
relie $f(\gamma)$ et $\delta*g(\gamma)*\overline{\delta}$.
Cette homotopie est décrite dans l’animation suivante.
Une application continue $f:X\to Y$ est une équivalence d’homotopie s’il existe une application continue $g:Y\to X$ telle $g\circ f$ soit homotope à $I=\mathrm{Id}_X$ et $f\circ g$ soit homotope à $\mathrm{Id}_Y$. On dit alors que $X$ et $Y$ ont le même type d’homotopie.
Si $f:X\to Y$ est une équivalence d’homotopie alors $f_*$ est un isomorphisme. Deux espaces ayant le même type d’homotopie ont donc des groupes fondamentaux isomorphes.
Les rétractions sont un exemple particulier d’équivalence d’homotopie. Soit $A$ une partie de $X$. On dit que $X$ se rétracte par déformation sur $A$ s’il existe une homotopie $H :I\times X\to X$ relative à $A$ reliant $\mathrm{Id}_X$ et une application $r$ telle que $r(X)=A$ ($r$ est alors appelée une rétraction). L’application $r : X\to A$ est alors une équivalence d’homotopie : il suffit de prendre pour application « réciproque » l’inclusion de $A$ dans $X$.
- L’anneau $A=\left\{(x,y)\in\mathbb R^2, \frac{1}{4}\leq x^2+ y^2\leq 4\right\}$ se rétracte par déformation sur le cercle unité. Son groupe fondamental est donc $\mathbb Z$. Par conséquent l’anneau et le disque unité ne sont pas homéomorphes.
- Pour tout $n\geq 1$, $\mathbb R^n\setminus\{0\}$ se rétracte par déformation sur $S^{n-1}$. Par conséquent, $\mathbb R^2\setminus\{0\}$ et $\mathbb R^n\setminus\{0\}$ et donc $\mathbb R^2$ et $\mathbb R^n$ ne sont pas homéomorphes si $n\geq 3$.
- On dit qu’un espace est contractile s’il se rétracte par déformation sur un point. Les espaces contractiles sont $1$-connexes.
- Le ruban de Möbius se rétracte par déformation sur son âme. Son groupe fondamental est donc $\mathbb Z$.
Groupoïde fondamental
On peut « oublier » le point base en définissant un objet plus général appelé groupoïde fondamental. Formellement un groupoïde est une catégorie dont les objets forment un ensemble et dont tous les morphismes sont inversibles. L’espace des classes d’homotopie de chemins à extrémités fixées possède naturellement un structure de groupoïde $\pi X $ :
- les objets sont les points de $X$
- les morphismes de $\pi X(x,y)$ sont les classes d’homotopies de chemins reliant $x$ à $y$ et l’élément neutre est le lacet constant
- la composition est donnée par la concaténation. Ainsi, tous les morphismes sont inversibles et l’inverse est donnée par le chemin inverse.
Toute la théorie peut alors se développer dans le cadre des groupoïdes : une application continue induit un morphisme de groupoïdes, l’approche par les revêtements est bien définie et il existe un théorème de van Kampen. Cette approche est développée dans [3].
L’étude de groupe fondamental par les lacets se poursuit avec les théorèmes de relèvement des chemins et des homotopies.