|
> Groupe fondamental > Groupe fondamental par les lacets > Relèvement des applications Relèvement des applications |
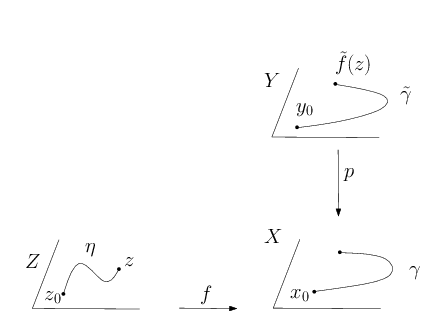
Soit $p : Y\to X$ un revêtement. On a vu dans le théorème de relèvement des chemins que toute application $\gamma : [0,1] \to X$ pouvait se relever à $Y$. En revanche, il n’est pas toujours vrai que le relevé d’un lacet soit fermé. Cela signifie en particulier qu’il n’est pas toujours possible de relever une application $S^1 \to X$. On va donner un critère simple pour déterminer si une application $f : Z \to X$ se relève ou non.
En tout cas, l’unicité (une fois choisi le relevé de l’origine) du relèvement s’étend à ce cadre général et la preuve est identique.
Soit $p : Y \to X$ un revêtement et $f : Z \to X$ une application, avec $Z$ connexe. On suppose qu’il existe deux relevés $\tilde{f}_1, \tilde{f}_2 : Z \to Y$ tels que $f = p \circ \tilde{f}_i$. Alors, si $\tilde{f}_1$ et $\tilde{f}_2$ coïncident en un point de $Z$, on a $\tilde{f}_1=\tilde{f}_2$.
$$\xymatrix{ && Y\ar[d]^{p} \\ Z \ar[rr]_f \ar[urr]^{\tilde{f}_1}_{\tilde{f}_2} && X.}$$
Un revêtement pointé $(Y, y_0) \to (X, x_0)$ définit un sous-groupe
$$ H(p, x_0, y_0) = p_*\left( \pi_1(Y, y_0) \right) \subset \pi_1(X, x_0)$$
isomorphe au groupe fondamental de la base (voir Revêtement et relèvement). S’il n’y a pas de risque de confusion, on pourra abréger la notation en $H(p)$. Ce sous-groupe est l’objet essentiel pour déterminer si une application donnée $f : Z \to X$ se relève en $\tilde{f} : Z \to Y$.
Soit $p : (Y, y_0) \to (X, x_0)$ un revêtement pointé, $Z$ un espace pointé connexe localement connexe par arcs et $f : (Z,z_0) \to (X, x_0)$ une application. Alors $f$ admet un relevé $\tilde{f} : (Z, z_0) \to (Y, y_0)$ si et seulement si
$$ f_*\left[ \pi_1(Z, z_0)\right] \subset p_*\left[\pi_1(Y, y_0)\right].$$
Soit $f : Y \to X$ un revêtement et $f : Z \to X$ une application, avec $Z$ simplement connexe. Alors il existe un relevé $\tilde{f} : Z \to Y$.
Nous allons donner deux preuves du théorème de relèvement des applications. La première est basée sur la théorie du groupe fondamental par les lacets. La seconde, plus abstraite, est dans l’esprit des revêtements.
Première démonstration du théorème de relèvement des applications. Si $f$ admet un relevé $\tilde{f}$ alors $p\circ\tilde{f}=f$ par conséquent $p_*\circ\tilde{f}_*=f_*$ et $f_*\left[ \pi_1(Z, z_0)\right] \subset p_*\left[\pi_1(Y, y_0)\right]$.
Réciproquement, soit $f:Z\to X$ une application continue telle que
$$ f_*\left[ \pi_1(Z, z_0)\right] \subset p_*\left[\pi_1(Y, y_0)\right].$$
On va construire $\tilde{f}$ explicitement. Soit $z \in Z$, on considère un lacet $\eta$ de $Z$ reliant $z_0$ et $z$, $\gamma$ l’image de $\eta$ par $f$ et $\tilde{\gamma}$ le relevé de $\gamma$ issu de $y_0$. On pose alors $\tilde{f}(z)=\tilde{\gamma}(1)$.
L’application $\tilde{f}$ est bien définie. En effet, soit $\eta'$ un autre chemin reliant $z_0$ à $z$, $\gamma'$ l’image de $\eta'$ par $f$ et $\tilde{\gamma'}$ le relevé de $\gamma'$ issu de $y_0$. On a alors
$$ [\gamma\cdot\gamma']=f_*([\eta\cdot\eta'])\in p_*\left[\pi_1(Y, y_0)\right].$$
Ainsi $\tilde{\gamma}(1)=\tilde{\gamma'}(1)$ et $f$ est bien définie. De plus $p(\tilde{f}(z))=\gamma(1)=f(\eta(1))$. Donc $p\circ\tilde{f}=f$.
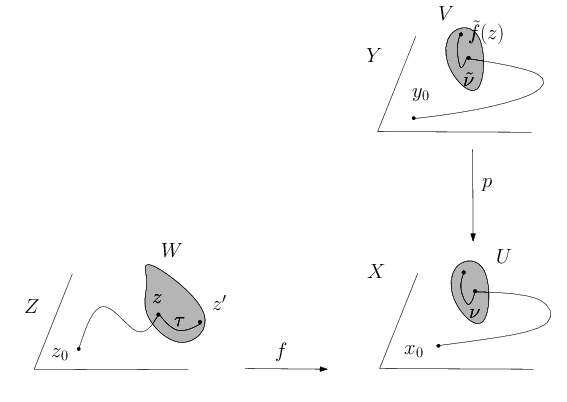
Enfin, $\tilde{f}$ est continue : soit $z\in Z$, $V$ un voisinage de $\tilde{f}(z)$ contenu dans l’image réciproque par $p$ d’un ouvert de trivialisation $U$ et $W$ un voisinage de $z$ connexe par arcs tel que $f(W)\subset U$. Si $z'\in W$, on considère un chemin $\tau$ de $W$ reliant $z$ à $z'$ et on pose $\nu=f(\tau)$. Alors le relevé $\tilde\nu$ de $\nu$ issu de $\tilde{f}(z)$ est contenu dans $V$ et $\widetilde{\gamma\cdot\nu}=\tilde{\gamma}\cdot\tilde{\nu}$. Ainsi $\tilde{f}(z')\in V$ et $f$ est continue. Donc $\tilde{f}$ est un relevé de $f$.
C.Q.F.D.
Seconde démonstration du théorème de relèvement des applications. Elle utilise le revêtement image réciproque. On commence donc par rappeler sa définition
Soit $p : Y\to X$ un revêtement et $f : X'\to X$ une application continue.
$$ \xymatrix{&& Y\ar[d]^{p} \\ X' \ar[rr]^f && X.}$$
On considère
$$Y'=\{(x',y)\in X'\times Y, f(x')=p(y)\}.$$
muni de la topologie induite par la topologie produit et on note $p' : Y'\to X'$ la projection sur la première coordonnée et $g : Y'\to Y$ la projection sur la seconde coordonnée. On obtient alors le digramme suivant
$$\xymatrix{Y'\ar[d]_{p'}\ar[rr]^{g}&& Y\ar[d]^{p} \\ X' \ar[rr]^f && X.}$$
Alors, le diagramme commute et l’application $p'$ est un revêtement. C’est le revêtement image réciproque.
Passons maintenant à la démonstration proprement dite. Si $f:Z\to X$ est une application continue telle que
$$ f_*\left[ \pi_1(Z, z_0)\right] \subset p_*\left[\pi_1(Y, y_0)\right] $$
on considère le revêtement image réciproque de $f$ :
$$ \begin{CD} (Y',(z_0,y_0)) @>g>>(Y,y_0)\\ @Vp'VV @VpVV\\ (Z,z_0) @>f>>(X,x_0) \end{CD} $$
On restreint $p'$ à la composante connexe de $Y'$ contenant $(z_0,y_0)$. Montrons que $p'$ est alors un homéomorphisme ce qui garantit l’existence d’un relevé de $f$. Pour cela, il suffit de montrer que $p'_*$ est surjective (voir Relèvement et revêtement). Soit donc $h \in\pi_1(Z,z_0)$. Comme l’action du groupe fondamental sur la fibre est compatible avec les morphismes de revêtements (voir Action sur la fibre et monodromie), on a
$$g((z_0,y_0)\cdot h)=y_0\cdot f_*(h)=y_0 $$
car $f_*\left[ \pi_1(Z, z_0)\right] \subset p_*\left[\pi_1(Y, y_0)\right]$ et $p_*\left[\pi_1(Y, y_0)\right]$ est le stabilisateur de $y_0$. Par conséquent $(z_0,y_0)\cdot h=(z_0,y_0)$ et $h$ est dans le stabilisateur de $(z_0,y_0)$. Donc $p'_*$ est surjective, $p'$ est un homéomorphisme et $f$ admet un relevé.
C.Q.F.D.