
|
> Homologie > Introduction à l’homologie via le bordisme > Quelques propriétés des groupes de bordisme Quelques propriétés des groupes de bordisme |
Dans cet article, on développe la théorie du bordisme présentée dans Introduction au bordisme. Sa lecture nécessite un peu de familiarité avec l’homologie. On donne ici des exemples de calculs du groupe de bordisme en dimension $2$ ainsi que des propriétés générales des groupes de bordisme.
Rappelons que si $n$ est un entier et $X$ un espace topologique, on appelle $n$-cycle de $X$ une application continue $f: M\to X$ d’une variété fermée orientée de dimension $n$ vers $X$. Deux cycles sont bordants s’il existe une variété à bord $V$ de dimension $n+1$, et une application continue vers $X$ dont la restriction au bord coïncide avec les deux cycles - en changeant l’orientation du deuxième. En passant au quotient, on définit un groupe abélien $\Omega_n(X)$ : le $n$-ème groupe de bordisme de $X$. A titre d’exercice, le lecteur pourra montrer que $\Omega_0(\{p\}) = {\bf Z}$.
Quelques calculs du groupe $\Omega_2(X)$
Deuxième groupe de bordisme d’une surfaces orientée
Commençons par supposer que $X$ est une surface orientée. Si $f : S\to X$ est un cycle, on peut considérer l’image réciproque d’une valeur régulière, qui est une variété compacte orientée de dimension $0$ c’est-à-dire une collection finie de points affectés de signes. On appelle degré de $f$ (en $x$) la somme de ces signes.
Si $f_0$ et $f_1$ sont bordants et $x$ est une valeur régulière pour $f_0$ et $f_1$ alors les degrés de $f_0$ et $f_1$ en $x$ sont les mêmes.
Le degré ne dépend pas du choix de $x$. On parle de degré de $f$.
Le lecteur est encouragé à démontrer ces résultats, par exemple en s’inspirant du cas de la dimension 1.
Le morphisme $\Omega_2(X) \to {\bf Z}$ donné par le degré est un isomorphisme.
La surjectivité est claire : l’identité est de degré 1 !
Pour l’injectivité, on considère $f: S \to X$ de degré nul. On choisit une valeur régulière $x$ de $f$ et on note $u_1,v_1,\ldots,u_n,v_n$ les pré-images de $x$ où les $u_i$ sont affectés du signe + et les $v_i$ du signe -. On recolle alors à $S\times [0,1]$ des cylindres $\mathbb{D}^2\times [0,1]$ en recollant $\mathbb{D}^2\times \{0\}$ sur un voisinage de $u_i$ dans $S\times \{0\}$ et $\mathbb{D}^2\times\{1\}$ sur un voisinage de $v_i$ dans $S\times \{0\}$. On obtient de la sorte une variété $N$ et $f$ se prolonge en une application $f:N\to X$. Le bord de $N$ est $S\amalg S'$ et $f$ restreinte à $S'$ évite un voisinage de $x$.
Le complémentaire d’un voisinage de $x$ dans $X$ est homotopiquement équivalent à un bouquet de cercles $B$ (vu ici comme une partie de $X$). On peut donc supposer que $f$ restreinte à $S'$ est à valeurs dans $B$ et lisse là où cela a du sens.
Prenons un valeur régulière sur chaque arête de $B$. Les images réciproques par $f_{|S'}$ de ces valeurs sont des unions de cercles tracés sur $S'$. Pour chacun de ces cercle, on considère un disque épaissi $\mathbb{D}^2\times [0,1]$ et on recolle le morceau de bord $(\partial\mathbb{D}^2)\times [0,1]$ sur un voisinage de notre cercle dans $S'$. L’application $f$ se prolonge à cette nouvelle variété de bord $S\amalg S''$. L’application $f$ restreinte à $S''$ évite un point sur chaque arête de $B$. Il ne reste alors plus qu’à boucher $S''$ en une 3-variété et à prolonger $f$ (l’idée est la même que pour le prolongement d’une fonction à valeurs dans un intervalle)...
Surfaces non orientables
Le cas non orientable est différent.
Si $X$ est une surface non orientable, $\Omega_2(X) =0$.
Contrairement au cas précédent, l’identité de $X$ n’est plus un 2-cycle puisque par hypothèse, l’espace de départ d’un cycle est orienté ! Plutôt que de démontrer le théorème, regardons simplement un exemple dans le cas $X=\mathbb{P}^2(\mathbb{R})$. Considérons l’application naturelle $p:\mathbb{S}^2\to \mathbb{P}^2(\mathbb{R})$ qui identifie deux points antipodaux et montrons que la classe de bordisme associée est triviale.
Fixons $\epsilon>0$ assez petit, et regardons la sous-variété à bord $M$ de $\mathrm{SO}_3$, constituée des rotations dont l’angle est compris entre $\epsilon$ et $2\pi-\epsilon$. Le bord de $M$ est formé des rotations d’angle $\epsilon$ (on peut renverser l’axe d’une rotation, une rotation d’angle $2\pi-\epsilon$ est donc aussi une rotation d’angle $\epsilon$), et isomorphe à $\mathbb{S}^2$ (une rotation d’angle fixé est décrit par son axe orienté, soit un élément de $\mathbb{S}^2$). La variété $M$ est par ailleurs orientable puisque $\mathrm{SO}_3$ l’est. Considérons alors l’application $f:M\to\mathbb{P}^2(\mathbb{R})$ qui à une rotation associe son axe. Elle prolonge bien la projection $p$ ; par conséquent, le $2$-cycle $p$ est trivial dans $\Omega_2(\mathbb{P}^2(\mathbb{R}))$ !
Un exemple plus élaboré : deuxième groupe de bordisme d’une variété de dimension 3
On se place maintenant dans le cas où $X$ est une variété fermée et orientée de dimension 3. Pour étudier les liens entre $\Omega_1(X)$ et $\Omega_2(X)$ nous allons généraliser la construction de forme d’intersection.
Si $f \in \Omega_1(X)$ et $g\in \Omega_2(X)$ on représente $f$ et $g$ par des cycles différentiables et transverses. Les points d’intersection sont affectés de signes $\pm 1$ et on considère la somme de ces signes : en un point d’intersection, l’espace tangent est la somme directe de l’espace tangent à $f$, qui est orienté, et de l’espace tangent à $g$, également orienté, on associe le signe $+$ à l’intersection si l’orientation obtenue correspond à celle de $X$ et le signe $-$ si les orientations ne correspondent pas.
Ceci définit une forme bilinéaire $\Omega_1(X) \times \Omega_2(X) \to {\bf Z}$.
La preuve est semblable au cas de l’intersection des 1-cycles et donc laissée au lecteur.
La dualité de Poincaré ne consiste pas en l’assertion que cette forme est non dégénérée... Pour s’en assurer, il suffit de considérer les exemples de variétés de dimension 3 pour lesquels $\Omega_1(X) $ possède des éléments de torsion. Si la forme d’intersection était non dégénérée, de tels éléments ne pourraient pas exister. La bonne formulation de la dualité est plus subtile : il faut oublier la torsion.
La forme bilinéaire $\left( \Omega_1(X)\otimes {\bf Q} \right) \times \left( \Omega_2(X) \otimes {\bf Q} \right) \to {\bf Q}$ est non dégénérée.
Pour montrer ce théorème, on veut pouvoir choisir des cycles particuliers.
Toute classe de $\Omega_2(X)$ est représentée par un plongement d’une surface (pas nécessairement connexe) dans $X$.
Par une petite perturbation, on peut supposer la classe représentée par $f: S \to X$ qui ne présente que les singularités suivantes.
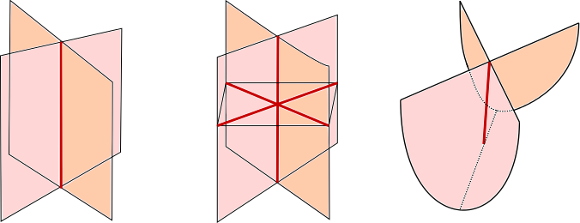
On peut éliminer toutes les singularités en faisant les modifications locales suggérées dans les dessins ci-dessous.
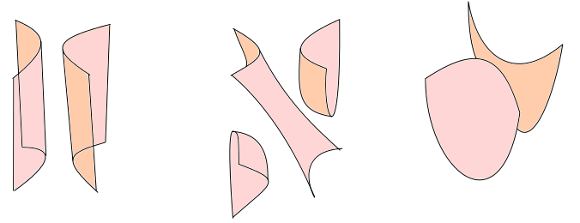
Les côtés rose et saumon indiquent les deux faces de $S$ qu’il faut respecter lors de la modification.
Considérons une classe non nulle de $\Omega_2(X)$ représentée par une surface plongée $f: S \to X$. Il existe une classe $g$ de $\Omega_1(X)$ dont le nombre d’intersection avec $f$ est non nul.
Supposons d’abord $S$ connexe et plongée dans $X$. Si le complémentaire de $S$ dans $X$ est connexe, il est facile de construire une courbe fermée qui ne coupe $S$ qu’une seule fois. Si le complémentaire n’est pas connexe, une composante du complémentaire définit un bordisme et la classe de $f$ est triviale ce qui contredit nos hypothèses.
Si $S$ n’est plus supposée connexe, on peut procéder de la manière suivante. Considérons le bord d’une composante connexe du complémentaire. C’est une surface dont certaines composantes sont orientées positivement par rapport à $S$ et d’autres négativement.
La figure suivante montre qu’en ajoutant des tubes et quitte à remplacer $S$ par un cycle cobordant $S'$, on peut se ramener au cas où chaque composante du complémentaire de $S$ a au plus deux composantes dans son bord.
S’il n’y a qu’une composante de bord, on peut l’éliminer puisqu’elle définit un bordisme. On est donc amené à la situation dans laquelle chaque composante du complémentaire a exactement deux composantes de bord, l’une positive et l’autre négative. Ces composantes sont donc disposées de manière cyclique.
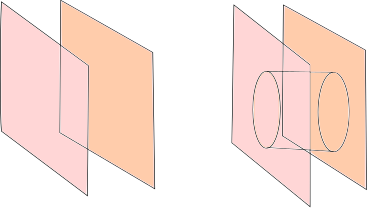
Il est alors facile de construire une courbe (la courbe rouge) qui intersecte $S$ exactement $n$ fois où $n$ est le nombre de composantes connexes de $S$.
Nous venons de voir que le morphisme
$$\Omega_2(X) \to {\rm Hom} (\Omega_1(X), {\bf Z})$$
est injectif. En particulier, on remarque que $\Omega_2(X)$ est sans torsion.
Considérons une classe de $\Omega_1(X)$ qui n’est pas de torsion, représentée par un $1$-cycle $f: C \to X$. Alors, il existe une classe $g$ de $\Omega_2(X)$ dont le nombre d’intersection avec $f$ est non nul.
Considérons un élément de $\Omega_1(X)$ qui n’est pas de torsion. Alors, il existe un morphisme $\Omega_1(X) \to {\bf Z}$ qui envoie notre élément sur un entier non nul. On peut alors voir ce morphisme comme un morphisme $\phi:\pi_1(X)\to {\bf Z}$ d’après ce théorème. Un tel morphisme se représente par une application $f$ de $X$ vers le cercle. Pour le voir, considérons une décomposition cellulaire de $X$ avec un seul sommet $x_0$ et posons $f(x_0)=1\in \mathbb{S}^1$. Chaque arête $e$ représente un élément de $\pi_1(X,x_0)$ et on définit $f$ en restriction comme faisant $\phi(e)$ tours du cercle. On peut alors prolonger $f$ aux autres cellules de $X$ (exercice).
On déforme alors $f$ en une application lisse et on en prend un niveau régulier : cela nous donne la surface que l’on cherche.
Le théorème est démontré !
Un théorème de Hopf
Si $X$ est un espace topologique, on considère l’ensemble des classes d’homotopie d’applications continues $\mathbb{S}^2 \to X$ envoyant un point $N$ fixé sur un point base de $X$ fixé. Cet ensemble, noté $\pi_2(X)$, est muni d’une structure de groupe abélien. Ce groupe (et ses analogues en dimension supérieure) sont présentés dans Groupes d’homotopie supérieurs.
Évidemment, chaque classe d’homotopie ${\bf S}^2 \to X$ définit une classe de bordisme de $\Omega_2(X)$ et on a un morphisme :
$$\pi_2(X) \to \Omega_2(X)$$
qui n’est en général ni surjectif ni injectif. Un théorème fondamental de Hopf, à l’origine de la cohomologie des groupes, montre que le conoyau de ce morphisme ne dépend que du groupe fondamental. Pour l’énoncer, exprimons le groupe fondamental $\pi_1(X)$ comme le quotient d’un groupe libre $L$ par un sous-groupe distingué $R$. C’est ce qu’on obtient lorsqu’on présente le groupe en termes de générateurs et relations. On note $[L,L]$ le sous-groupe normal de $L$ engendré par les commutateurs et $[L,R]$ celui engendré par les commutateurs d’éléments de $L$ et de $R$.
Le quotient de $ \Omega_2(X)$ par l’image de $\pi_2(X)$ est isomorphe à $[L,L] \cap R / [L,R]$.
Par exemple, si $X$ est simplement connexe, l’application est surjective.
Commençons par le cas $X$ simplement connexe. Soit $f : S \to X$ un 2-cycle. Si $S$ n’est pas une sphère, on trace sur $S$ une courbe fermée simple qui ne déconnecte pas. On découpe $S$ et on remplit les bords par des disques puisque $X$ est simplement connexe. On a donc trouvé un cycle $g$ équivalent à $f$ défini sur une surface de genre inférieur. Ceci permet de représenter $f$ par un cycle défini sur une sphère.
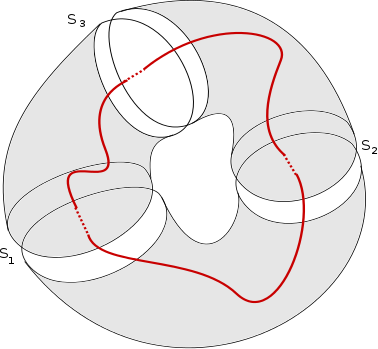
Le cas général, bien qu’un peu plus délicat, est dans le même esprit. Soit $f : S \to X$ un 2-cycle défini sur une surface de genre $g$ et considérons l’application induite au niveau des groupes fondamentaux, par exemple comme dans la figure suivante.
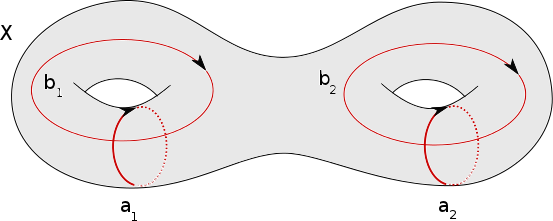
Le produit $[a_1,b_1][a_2,b_2]$ est trivial dans $\pi_1(S)$ donc dans $\pi_1(X)=L/R$.
C’est donc un élément de $R \cap [L,L]$. Il reste à voir que l’application ainsi définie est un isomorphisme, ce qui est laissé au lecteur. [1]
Un peu de généralité : quelques propriétés des groupes de bordismes
Les groupes de bordismes ne vérifient pas exactement ce qu’on attend d’une homologie, néanmoins ces groupes partagent beaucoup de propriétés.
Jusqu’ici tout va bien
La définition des groupes de bordisme se généralise au cas relatif. On se donne un sous-espace $Y \subset X$ de $X$. On appelle $n$-cycle relatif une application continue $f : M \to X$ d’une variété à bord vers $X$ qui envoie le bord dans $Y$. La définition du bordisme s’étend immédiatement, et on obtient des groupes de bordismes relatifs, notés $\Omega_n(X,Y)$.
Il est clair que si $\phi : X_1 \to X_2$ est une application continue, tout cycle de $X_1$ définit par composition avec $\phi$ un cycle de $X_2$. On obtient donc un morphisme $\phi_{\star} : \Omega_n(X_1) \to \Omega_n(X_2)$.
Voici quelques propriétés, dont les preuves sont faciles...
Les définitions précédentes font de $\Omega_n$ un foncteur de la catégorie des espaces topologiques vers celle des groupes abéliens. Mieux encore, deux applications homotopes induisent les mêmes morphismes au niveau des groupes de bordismes. Il s’agit donc d’un foncteur de la catégorie homotopique.
Si $Y \subset X$, on peut restreindre un cycle relatif à son bord, pour obtenir un cycle (absolu) de $Y$ de dimension $n-1$. On obtient ainsi un morphisme naturel $\Omega_n(X,Y) \to \Omega_{n-1}(Y)$.
La suite suivante est exacte.
$$ \cdots \to \Omega_{n}(X,Y) \to \Omega_{n-1}(Y) \to \Omega_{n-1}(X)\to \Omega_{n-1}(X,Y) \to \cdots $$
Soit $Z \subset Y \subset X$ trois variétés emboitées, éventuellement à bord de même dimensions. L’application naturelle $\Omega(X \setminus Z, Y \setminus Z)) $ dans $\Omega(X , Y) $ est un isomorphisme.
Les problèmes commencent
La théorie de l’homologie associe des groupes abéliens à un espace topologique. Il va de soi qu’on n’attend pas grand-chose de la topologie d’un point si bien qu’il est naturel de demander que l’homologie du point soit triviale. La théorie du bordisme ne possède malheureusement pas cette propriété à partir de la dimension 4.
$\Omega_n(\{p\}) = 0$ pour $n=1,2,3$ mais $\Omega_4(\{p\})$ est non trivial.
Nous avons déjà discuté des cas $n=1,2$. Les cas $n=3,4$ ne sont pas faciles et sont discutés ailleurs [2]. Le fait que toute variété fermée orientée de dimension 3 est le bord d’une variété de dimension 4 résulte d’un description des diagrammes de Heegard et d’une discussion du groupe de difféotopies. Le plan projectif complexe est une variété fermée orientée de dimension 4 qui n’est pas un bord. La démonstration n’est pas facile à ce stade puisqu’elle requiert la dualité de Poincaré [3].
On note en général $\Omega_n$ le groupe de bordisme du point, c’est-à-dire l’ensemble des variétés fermées orientées de dimension $n$ modulo la relation de « cobordisme » : $M$ et $M'$ sont cobordantes s’il existe une variété dont le bord est $M\amalg\overline{M'}$, i.e. est constitué de $M$ et de $M'$ avec l’orientation opposée. La somme directe $\Omega=\bigoplus_{n \geq 0}\Omega_n$ est naturellement un anneau gradué. Il suffit d’utiliser le produit cartésien des variétés : si $M$ et $M'$ sont cobordantes, alors $M\times V$ et $M'\times V$ le sont également pour toute variété fermée $V$. La structure de cet anneau est assez bien comprise (voir [4]). Le produit tensoriel $\Omega \otimes {\bf Q}$ est isomorphe à une algèbre de polynômes engendrée par des éléments $x_n$ de degré $4n$.
Bordisme et homologie singulière
Cette section est destinée aux lecteurs ayant appris la définition de l’homologie singulière. Il s’agit de comparer bordisme et homologie.
Il y a bien sûr une application naturelle $\phi: \Omega_n(X) \to H_n(X)$ pour tout espace topologique $X$ et pour tout $n \geq 0$. Nous savons que cette application n’est pas un isomorphisme pour $n=4$ et $X$ un point.
L’application $\phi$ est un isomorphisme pour $n=0,1,2,3$ et une surjection pour $n=4$.
Nous l’avons essentiellement déjà démontré pour $n=0,1$.
Le cas $n=2$ est déjà intéressant. Montrons d’abord que $\phi:\Omega_2(X) \to H_2(X)$ est surjective. Une classe de $H_2(X)$ est représentée par un 2-cycle singulier, lui-même étant une somme d’un certain nombre de 2-simplexes singuliers $\sum_{i=1}^k \sigma_i$. Considérons la réunion disjointe $S$ de $k$ copies du simplexe standard de dimension 2. La donnée des applications $\sigma_i$ permettent de construire une application $f$ de $S$ vers $X$. Le fait que nous considérons un cycle, i.e. que la somme $\sum \partial \sigma_i$ soit nulle, signifie qu’on peut identifier les $3k$ arêtes du bord de $S$ deux par deux de façon compatible avec $f$. Recollons ces arêtes deux par deux pour obtenir un $2$-complexe $\overline{S}$ et une application continue $\bar{f}$ de $\bar{S}$ vers $X$.
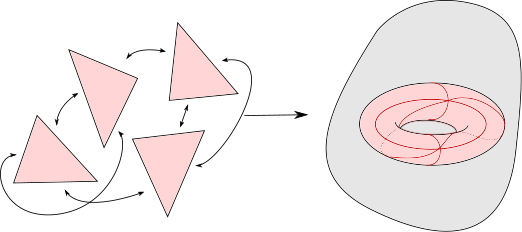
Le $2$-complexe $\bar{S}$ est une surface orientée et on dispose d’une application continue de $\bar{S}$ vers $X$, qui représente la classe d’homologie initiale, ce qui montre bien que $\phi$ est surjective.
Pour la surjectivité de $\phi$ quand $n=3$, on procède de la même manière. On commence donc avec une réunion disjointe de $3$-simplexes dont on recolle les faces deux par deux. Le 3-complexe obtenu n’est pas une $3$-variété à cause du voisinage des sommets. En effet, au voisinage d’un point d’une arête, on obtient un collage de tétraèdres comme sur la figure ci-dessous.
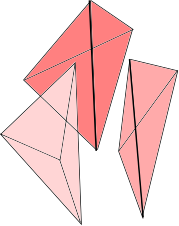
Au voisinage des sommets, on voit le cône sur une surface, qui n’est une 3-variété que s’il s’agit du cône sur une sphère. Mais nous savons que toute surface orientée borde une 3-variété. On remplace donc ce cône par une $3$-variété, recollée le long du bord, pour produire une 3-variété fermée qui représente le $3$-cycle dont on est partis.
Pour $n=4$, en s’aidant du fait que $\Omega_4 ={\bf Z}$, on procède (presque) de la même manière. Exercice !
En ce qui concerne l’injectivité pour $n=1,2,3$, la preuve est presque la même. On dispose d’une classe de bordisme $M \to X$ dont on sait qu’elle est homologiquement triviale (dans l’homologie singulière) et il faut montrer qu’elle borde. Pour cela, on triangule la variété $M$, on exprime le cycle singulier correspondant comme un bord, et on modifie ce bord pour le transformer en une variété en utilisant les mêmes outils que précédemment.
Le lien entre bordisme et homologie dans toutes les dimensions est bien plus compliqué. Il s’exprime en termes d’une suite spectrale $E_{p,q}^r$ dont le terme $E_{p,q}^1(X)$ est $H_p(X) \otimes \Omega_q$ et qui converge vers $\Omega_{p+q} (X)$.
[1] On renvoie à l’exercice 4, p.46 de l’ouvrage Cohomology of Groups de K. Brown
[2] J. W. Milnor and J. D. Stasheff, Characteristic Classes, Princeton University Press, Chapter 17
[3] Il faut pour cela introduire la signature d’une variété de dimension 4 : la dualité de Poincaré montre que toute variété qui borde est de signature 0, tandis que celle de $\mathbb{P}^2(\mathbb{C})$ est égale à 1.
[4] Wall, Determination of the cobordism ring, Ann. of Math. 72 (1960), 292–311
