
|
> Homologie > Introduction à l’homologie via le bordisme > Introduction au bordisme : définition ; étude du premier groupe de (...) Introduction au bordisme : définition ; étude du premier groupe de bordisme |
Cet article présente le bordisme, une théorie à priori plus intuitive que l’homologie et guidée par la même idée : mesurer la complexité de la topologie d’une variété $X$ en comptant, pour chaque entier $p$ entre $0$ et $\mathrm{dim}(X)$, le nombre maximal de sous-variétés fermées de dimension $p$ que l’on peut « faire entrer » dans $X$, sans que certaines de ces sous-variétés, correctement orientées, ne forment le bord orienté d’une sous-variété de dimension $p+1$. On s’intéresse ici principalement aux cas $p=1$ et $p=2$ . Des exemples plus sophistiqués en dimension $2$ (et plus) sont étudiés dans l’article Le bordisme en dimension 2 (et plus).
Définition du premier groupe de bordisme
Soit $X$ un espace topologique. Nous allons lui associer un groupe abélien $\Omega_1(X)$ qui rend compte des courbes dans $X$.
On appelle $1$-cycle dans $X$ la donnée d’une variété fermée (compacte sans bord) orientée $C$ de dimension 1 et d’une application continue $f: C \to X$. Notez que $C$ est la réunion disjointe d’un certain nombre de copies du cercle, si bien que $f$ se résume à la donnée d’un certain nombre de courbes fermées et orientées dans $X$.
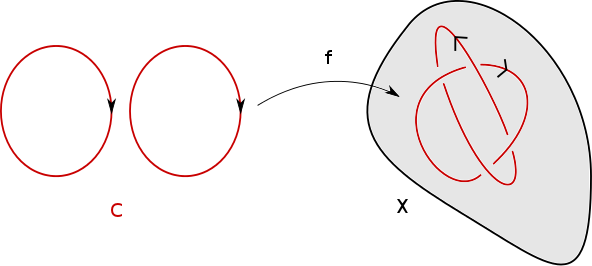
On note $\overline{C}$ ou $-C$ la variété $C$ munie de l’orientation opposée.
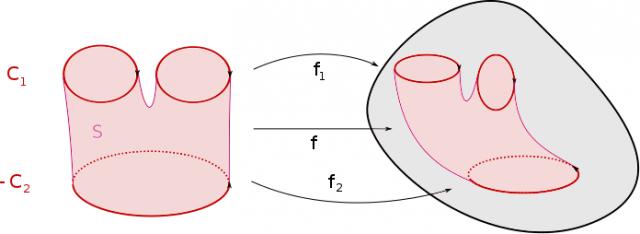
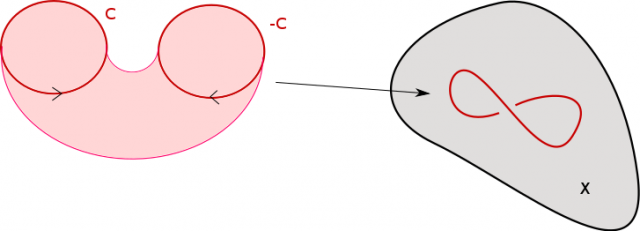
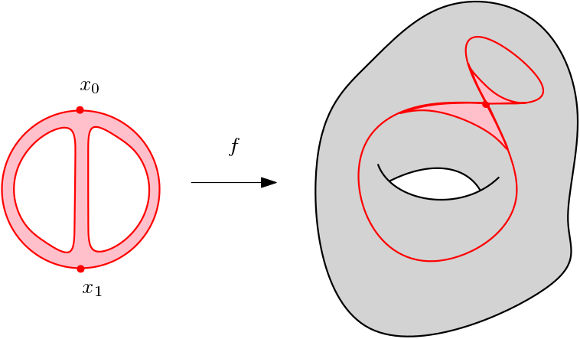
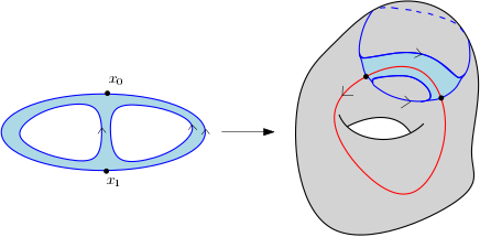
On dit que deux cycles $f_1 : C_1\to X$ et $f_2 : C_2 \to X$ sont bordants s’il existe une surface orientée à bord $S$, dont le bord orienté est la réunion de $C_1$ et $\overline{C}_2$ et une application continue $f : S \to X$ dont la restriction à $C_1,\overline{C}_2$ est égale $f_1,f_2$.
La figure suivante montre un exemple de cycles bordants.
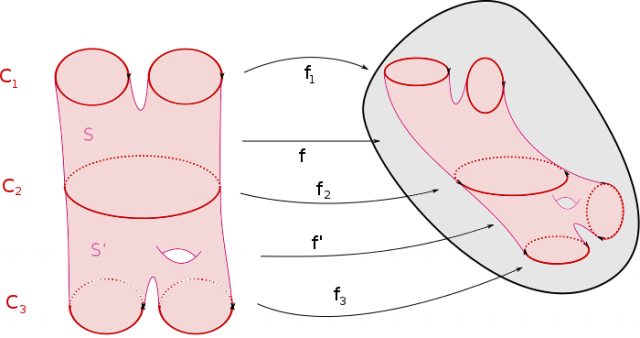
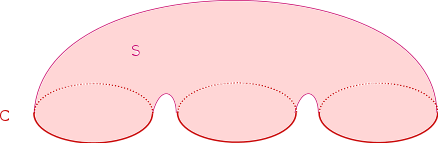
Le bordisme est une relation d’équivalence, comme le montre la figure suivante.
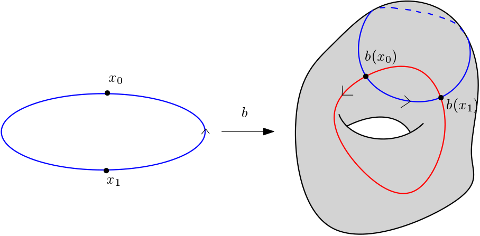
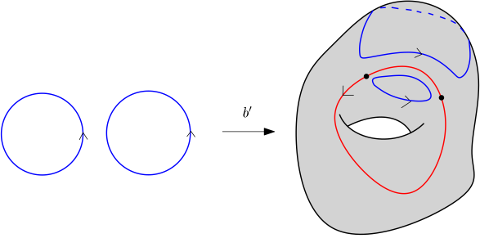
On note $\Omega_1(X)$ l’ensemble des classes de bordismes. Étant donnés deux cycles $f_1 : C_1\to X$ et $f_2 : C_2 \to X$, on peut les « ajouter », c’est-à-dire considérer l’application $f_1\oplus f_2$ définie sur la réunion disjointe de $C_1$ et $C_2$. Cette opération sur les cycles passe au quotient sur $\Omega_1(X)$ comme le montre la figure suivante.
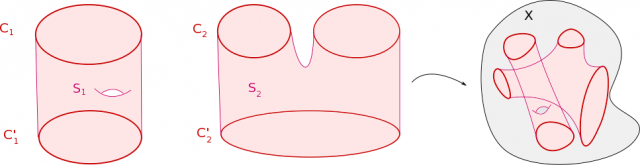
En effet, si $S_1$ rend $C_1$ et $C'_1$ bordants tandis que $S_2$ rend $C_2$ et $C'_2$ bordants, alors $S_1\amalg S_2$ rend $C_1\amalg C_2$ bordant avec $C'_1\amalg C'_2$.
Équipé de cette opération, $\Omega_1(X)$ devient un groupe abélien. L’élément neutre est l’application vide définie sur l’ensemble vide (qui est bien une variété de dimension 1 par convention). L’existence d’un opposé pour le $1$-cycle $f : C\to X$ est justifiée par la figure suivante qui décrit un cobordisme entre $C\amalg\overline{C}$ et l’ensemble vide. La surface reliant $C$ à $\overline{C}$ est difféomorphe à $C\times [0,1]$ et on peut prendre comme cobordisme $F(x,t)=f(x)$ d’image $f(C)$.
Le groupe abélien $\Omega_1(X)$ est le premier groupe de bordisme de la variété $X$.
L’addition de $\Omega_1(X)$ se notera simplement + et on désigne souvent la classe de $f$ simplement par la lettre $f$ s’il n’y a pas de confusion possible. Comme expliqué plus haut, notre but véritable est d’introduire des groupes d’homologie et le bordisme ne sert ici que de motivation. Le lecteur doit cependant savoir que les premiers groupes $\Omega_1(X)$ et $H_1(X, {\bf Z})$ sont isomorphes.
Quelques exemples simples
Le premier groupe de bordisme du point
Commençons par une remarque simple mais importante. Toute variété fermée orientée $C$ de dimension 1 est le bord d’une variété orientée $S$ de dimension 2. C’est clair !
Nous pouvons donc affirmer que le premier groupe de bordisme $\Omega_1(\{p\})$ d’un point $p$ est le groupe trivial ! Toute application constante définie sur $C$ se prolonge à une application (constante !) sur $S$. Elle définit donc la classe de bordisme triviale. Cette observation, triviale en dimension 1, sera la source des difficultés que nous rencontrerons en dimensions supérieures.
Le premier groupe de bordisme du cercle
Nous abordons maintenant la description de $\Omega_1(X)$ dans le cas où $X$ est le cercle ${\bf S}^1$. Nous allons montrer que $\Omega_1({\bf S}^1)$ est isomorphe à $\mathbb Z$ et qu’un isomorphisme est donné par le degré. Pour cela, nous allons commencer par démontrer quelques lemmes dont l’usage s’avérera utile dans des situations bien plus générales.
Choix d’un représentant connexe et lisse
Si $X$ est connexe, toute classe de bordisme est représentée par un cycle défini sur une variété fermée orientée connexe de dimension 1, c’est-à-dire est représentée par une application continue $f: {\bf S}^1 \to X$.
Montrons qu’un cycle $f:C_1\amalg C_2\to X$ (où $C_1$ et $C_2$ sont des cercles) est cobordant à un cycle $g : C_1\# C_2\to X$. Dans le cas général, on conclut par récurrence sur le nombre de cercles.
On choisit $x_1\in C_1$ et $x_2\in C_2$ et on considère un pantalon de bord $C_1\amalg C_2$ et $C_1\# C_2$ comme sur la figure.
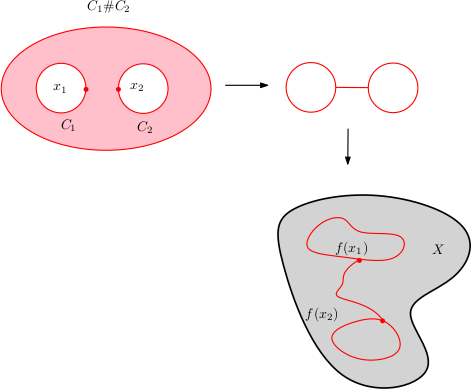
Il nous reste à construire une application continue du pantalon dans $X$ qui prolonge $f$. Pour cela on commence par retracter le pantalon sur les cercles $C_1$ et $C_2$ reliés par un segment et on prolonge $f$ au segment en utilisant un chemin reliant $f(x_1)$ à $f(x_2)$ (un tel chemin existe car $X$ est connexe par arcs).
C.Q.F.D.
Deux cycles homotopes sont cobordants.
Soient $f_0$ et $f_1$ deux cycles reliés par l’homotopie $H:C\times[0,1]\to X$ où $f_0(x)=H(x,0)$ et $f_1(X)=H(x,1)$. On reconnaît là un cas particulier de la relation de bordisme !
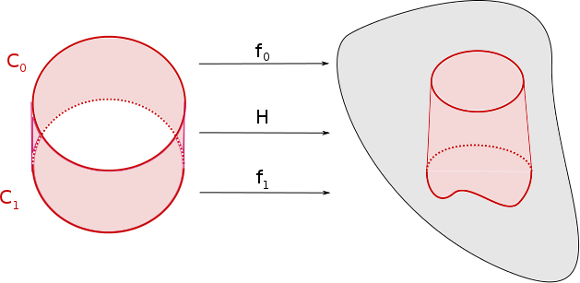
C.Q.F.D.
Soit $f : C \to X$ un cycle. Tout cycle $g : C \to X$ suffisamment proche de $f$ est bordant à $f$. En particulier, tout cycle est bordant à un cycle différentiable.
Les applications lisses sont denses dans les applications continues et l’espace des applications continues est localement connexe par arcs. Par conséquent, toute application continue est homotope à une application lisse. On peut alors appliquer le lemme précédent.
C.Q.F.D.
Degré d’un cycle $f:C \to{\bf S}^1$
Nous définissons ici, de manière élémentaire, le degré d’un $1$-cycle. On trouvera ici une présentation plus générale du degré d’une application, qui nécessite de connaitre les bases de la théorie de l’homologie singulière.
Soit $f : C\to {\bf S}^1$ un cycle lisse. L’image réciproque d’une valeur régulière $x \in {\bf S}^1$ est une variété orientée de dimension 0, c’est à dire un ensemble fini de points. Un choix d’orientation pour une variété de dimension $0$ revient à attribuer un signe à chacun des points de la variété. Notons provisoirement $\mathrm{deg}_x(f)$ la somme de ces signes.
Si $f_1 : C_1 \to {\bf S}^1$ et $f_2 : C_2 \to {\bf S}^1$ sont bordants et si $x$ est une valeur régulière pour $f_1$ et $f_2$ alors $\mathrm{deg}_x(f_1)=\mathrm{deg}_x(f_2)$.
On prend un bordisme $F : S\to X$ prolongeant $f_1$ et $f_2$ et on le perturbe (relativement au bord) pour que $x$ soit une valeur régulière. L’ensemble $F^{-1}(\{x\})$ est alors une sous-variété de dimension $1$, à bord, orientée et plongée dans $S$. En particulier $F^{-1}(\{x\})$ est formé de cercles orientés dans l’intérieur de $S$ et d’arcs orientés reliant les composantes de bord de $S$. Les arcs de $F^{-1}(\{x\})$ étant orientés, on peut associer un signe à leurs extrémités. Comme un arc a toujours deux extrémités, la somme de ces signes est nulle.
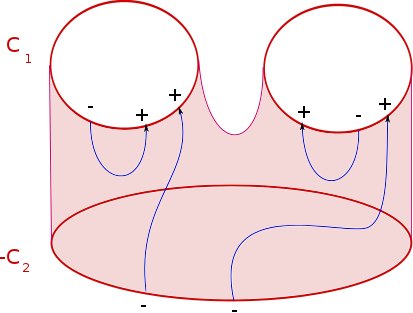
Or, sur $C_1$, ces signes correspondent à l’orientation de $f_1^{-1}(\{x\})$ et leur somme est donc $\mathrm{deg}_{x}(f_1)$. Le second bord de $S$ est $\overline{C_2}$ et la somme des signes associés à $f_2^{-1}(\{x\})$ nous donne donc $-\mathrm{deg}_{x}(f_2)$. On a donc bien $\mathrm{deg}_{x}(f_1)=\mathrm{deg}_x(f_2)$.
C.Q.F.D.
Le degré $\mathrm{deg}_x(f)$ ne dépend pas de $x$. On appelle cet entier le degré de $f$ et on le note $\mathrm{deg}(f)$. Ceci définit un homomorphisme $\mathrm{deg} : \Omega_1({\bf S}^1) \to {\bf Z}$.
Soient $x_0$ et $x_1$ deux valeurs régulières de $f$. On compose alors $f$ par une rotation $\rho$ qui envoie $x_0$ sur $x_1$, et on note $g=f\circ \rho$. On a alors $\mathrm{deg}_{x_0}(f)=\mathrm{deg}_{x_1}(g)$. En outre, les applications $f$ et $g$ sont alors homotopes (l’homotopie s’obtient en composant $f$ par un chemin de rotations qui joint l’identité à $\rho$) et $\mathrm{deg}_{x_1}(f)=\mathrm{deg}_{x_1}(g)$. On obtient donc le résultat voulu.
C.Q.F.D.
Description de $\Omega_1({\bf S}^1)$
L’application $\mathrm{deg} : \Omega_1({\bf S}^1) \to {\bf Z}$ est un isomorphisme.
Pour montrer la surjectivité, il suffit de remarquer que l’application $z\mapsto z^n$ de $\bf{S}^1$ dans lui-même est de degré $n$.
Passons à la preuve de l’injectivité. Considérons un $1$-cycle $f :C\to\bf{S}^1$ de degré $0$. D’après un lemme ci-dessus, on peut supposer $f$ définie sur le cercle $\mathbb{S}^1$. Notons $\pi:\mathbb{R}\to\mathbb{S}^1$ la projection usuelle donnée par $\pi(x)=e^{2i\pi x}$. On peut alors relever $f:\mathbb{S}^1\to\mathbb{S}^1$ en une application continue $\tilde f:\mathbb{R}\to \mathbb{R}$ (voir, par exemple, ici) vérifiant $\pi\circ \tilde f=f\circ \pi$. De l’égalité $\pi^{-1}(\{\pi(x)\})=x+\mathbb{Z}$, on tire qu’il existe un entier $n_x$ tel que $\tilde f(x+1)=\tilde f(x)+n_x$. De plus, par continuité de $\tilde f$, cet entier ne dépend pas du point $x$ ; notons-le donc $n$. En fait, cet entier $n$ n’est autre que le degré de $f$ (exercice !) ; il est donc nul. Autrement dit, on a $\tilde f(x+1)=\tilde f(x)$ pour tout $x$. L’application $\tilde F:\mathbb{R}\times [0,1]\to\mathbb{R}$ donnée par $\tilde F(x,t)=t\tilde f(x)$ définit une homotopie entre $\tilde f$ et l’application constante qui envoie tous les points sur $0$. Comme on a $\tilde F(x+1,t)=\tilde F(x,t)$, l’homotopie $\tilde F$ se projette en une homotopie $F:\mathbb{S}^1\times [0,1]\to\mathbb{S}^1$ entre $f$ et une application constante. Il en résulte que $f$ est bordante à une application constante, et donc triviale dans $\Omega_1({\bf S}^1)$.
C.Q.F.D.
Plus intéressant : Le premier groupe de bordisme d’une surface
On aborde maintenant le cas où $X$ est une surface orientée de genre $g$.
Description de $\Omega_1(X)$
Bien sûr, si $g=0$, c’est-à-dire si $X$ est une sphère, $\Omega_1({\bf S}^2)$ est trivial. En effet, dans une classe de bordisme on peut choisir un cycle différentiable. Ce cycle évite au moins un point de la sphère (et même beaucoup). Son image est donc contenue dans la sphère privée d’un point, difféomorphe au plan. Notre cycle est donc homotope à une application constante et la classe associée est triviale.
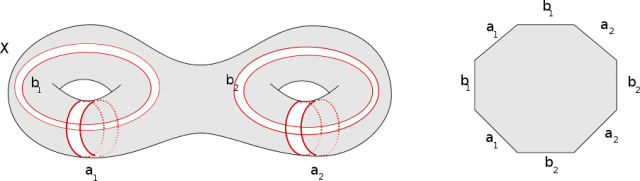
Dans toute la suite, on considère une surface qui n’est pas une sphère. On trace alors $2g$ courbes $a_1,b_1, \ldots, a_g,b_g$ sur $X$ comme sur la figure suivante (dans le cas $g=2$).
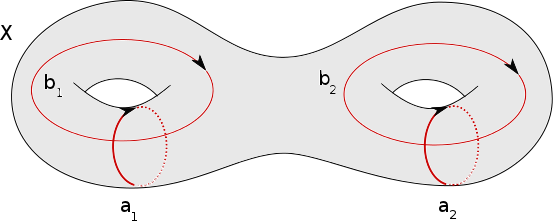
Chacune de ces courbes définit une classe de bordisme. Nous allons montrer le résultat suivant.
L’application
$$\begin{array}{rcl} {\bf Z}^{2g} & \longrightarrow & \Omega_1(X_g)\\ (m_1,n_1, \ldots, m_g,n_g) &\longmapsto & m_1 a_1 + n_1 b_1 + \ldots m_g a_g + n_g b_g \end{array} $$
est un isomorphisme.
Pour démontrer cela, nous allons construire un morphisme inverse. Ce morphisme est obtenu à l’aide de la forme d’intersection.
Le point important est le concept d’intersection de deux cycles sur une surface orientée. Soient $f_0$, $f_1$ deux cycles sur $X$. Par une perturbation arbitrairement petite (et donc sans changer la classe de bordisme), on peut supposer que $f_0$ et $f_1$ sont des immersions transverses. On associe un signe $\pm 1$ à chaque intersection de $f_0(C_0)$ et $f_1(C_1)$ : soit $y$ un point d’intersection, comme $C_0$ et $C_1$ sont orientés, la tangente à $f_0(C_0)$ en $y$ est dirigée par un vecteur $u_0$ et la tangente à $f_1(C_1)$ en $y$ est dirigée par un vecteur $u_1$. On attribue le signe $+$ à l’intersection si $(u_0,u_1)$ est une base directe et le signe $-$ sinon. La somme des signes aux différents points d’intersections sera appelée nombre d’intersection de $f_0$ et $f_1$.
Le nombre d’intersection de $f_0$ et $f_1$ ne dépend que des classes de bordismes de $f_0$ et $f_1$ et définit une application bilinéaire alternée $\Omega_1(X_g) \times \Omega_1(X_g) \to\mathbb{Z}$, appelée forme d’intersection et notée $f_0.f_1$.
Commen\c cons par généraliser la notion de nombre d’intersection. Soient $V$ et $W$ sont deux sous-variétés d’une même variété $U$, qu’on suppose transverses et de dimensions complémentaires (c’est-à-dire telles que $\mathrm{dim}(V)+\mathrm{dim}(W)=\mathrm{dim}(U)$). À chaque point d’intersection $y$ de $V$ et $W$ : on considère une base directe $\mathcal{B}_V$ de $T_y V$, une base directe $\mathcal{B}_W$ de $T_y W$, et on affecte à $y$ le signe $\pm 1$ selon que la concaténation des bases $\mathcal{B}_V$ et $\mathcal{B}_W$ est une base directe ou indirecte de $T_y U$. Le nombre d’intersection de $V$ et $W$ est la somme de ces signes.
Soit maintenant $f'_0$ tel que $f_0$ et $f'_0$ soient bordants. On veut montrer que le nombre d’intersection de $f_0'$ et $f_1$ est le même que celui de $f_0$ et $f_1$. Pour ce faire, on considère un bordisme $F_0 : S_0\to X$ entre $f_0$ et $f'_0$. Le nombre d’intersection de $f_0$ et $f_1$ peut se réinterpréter en considérant le nombre d’intersection de $ f_0\times f_1 : C_0\times C_1\longrightarrow X\times X$ avec la diagonale de $X\times X$ (exercice !). On notera que cette intersection est transverse car $f_0$ et $f_1$ se coupent transversalement. Quitte à perturber $F_0$, le produit
$$ F_0\times f_1 : S_0\times C_1\longrightarrow X\times X$$
est transverse à la diagonale de $X\times X$, et la pré-image par $ F_0\times f_1$ de la diagonale de $ X\times X$ est donc une sous-variété compacte de dimension 1 dans $S_0\times C_1$. Cette sous-variété consiste en un nombre fini de courbes fermées et un nombre fini d’arcs qui vont du bord de $S_0\times C_1$ au bord de $S_0\times C_1$. On finit l’argument comme pour l’invariance du degré.
Nous pouvons maintenant énoncer la toute première version de ce qui deviendra le théorème de dualité de Poincaré.
La forme d’intersection est non dégénérée.
Preuve.
Il s’agit de démontrer que si le nombre d’intersection d’un cycle donné $f$ avec tous les cycles est nulle, il représente 0 dans $\Omega_1(X_g)$. Commençons par voir que l’on peut choisir des représentants judicieux.
Tout cycle est bordant à une somme de courbes connexes et plongées.
Soit $f$ un cycle de $X_g$. Quitte à le perturber, on peut le supposer connexe et immergé, c’est à dire que $f:S^1\to X$ est une immersion avec un nombre fini de points doubles. On va éliminer un par un les points doubles.
Soit $x_0$ et $x_1$ deux points du cercle tels que $f(x_0)=f(x_1)$.
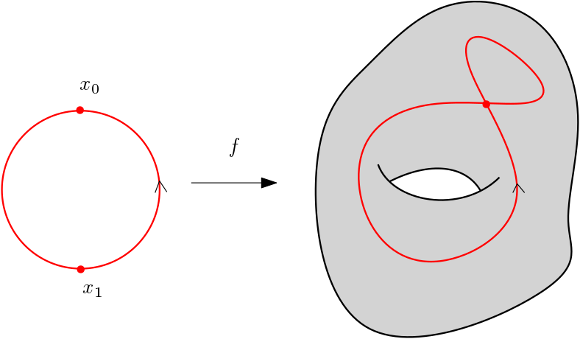
On montre que $f$ est cobordante à une application ayant un point double de moins. Pour cela, on construit un cobordisme de type pantalon, c’est à dire ayant pour source un pantalon.
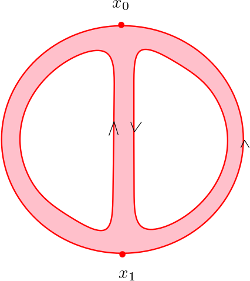
Voici une représentation du cobordisme en zoom et en couleur.
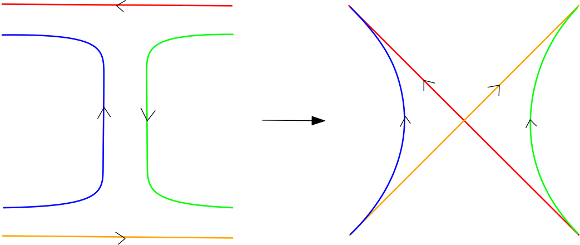
Et voici le même cobordisme vu de plus loin.
Soit $a$ et $b$ deux cycles de $X_g$ représentés par des courbes plongées avec $a$ connexe. Si $a.b=0$, alors $b$ est bordant à un cycle $b'$ dont l’image ne rencontre pas $a$.
On peut supposer que $a$ et $b$ se coupent transversalement. Considérons le long de $a$ deux croisements consécutifs et de signe opposés : ils existent bien puisque la somme des signes est nulle et $a$ est connexe.
On a alors le dessin suivant.
On peut alors remplacer $b$ par une courbe $b'$ comme sur le dessin.
Le cobordisme entre $b$ et $b'$ est décrit sur la figure suivante.
Par construction, $b'$ coupe $a$ en deux points de moins. On conclut alors par récurrence.
C.Q.F.D.
Supposons maintenant le nombre d’intersection d’un cycle donné $f$ avec tous les cycles, en particulier avec les $a_i,b_i$ est nulle. On peut donc construire un cycle $f'$, dans la même classe de bordisme, qui ne rencontre pas les $a_i,b_i$. Lorsqu’on découpe la surface $X_g$ le long des $a_i,b_i$, on obtient un disque comme le montre la figure ci-dessous si bien que toute application à valeurs dans ce disque est homotope à une constante.
Ceci termine le preuve de la non-dégénérescence de la forme d’intersection.
C.Q.F.D.
En utilisant la forme d’intersection, chaque élément $f$ de $\Omega_1(X_g)$ définit un morphisme
$$f^{\sharp} : g\in \Omega_1(X_g) \mapsto g.f \in {\bf Z}$$
En particulier, pour tout $i$,
- $a_i^\sharp(a_j)=0$ pour tout $j$
- $a_i^\sharp(b_i)=-1$
- $a_i^\sharp(b_j)=0$ pour tout $j\neq i$.
Il existe une formule symétrique pour $b_i^\sharp$. Ainsi l’application $f\mapsto f^\sharp$ est surjective. Le théorème précédent garantit l’injectivité. On a donc obtenu le résultat suivant.
L’application $f\mapsto f^\sharp$ est un isomorphisme.
Revenons à la description de $\Omega_1(X_g)$. On sait maintenant construire la réciproque de l’application
$$ (m_1,n_1, \ldots, m_g,n_g) \in {\bf Z}^{2g} \mapsto m_1 a_1 + n_1 b_1 + \ldots m_g a_g + n_g b_g \in \Omega_1(X_g), $$
c’est l’application
$$ c\in \Omega_1(X_g) \mapsto (-c\cdot b_1, c\cdot a_1, \ldots, -c\cdot b_g, c\cdot a_g) \in {\bf Z}^{2g}. $$
On a donc démontré le théorème décrivant le premier groupe de bordisme d’une surface.
C.Q.F.D.
Lien avec le groupe fondamental
Le théorème suivant explicite la relation entre le groupe fondamental d’un espace $X$ et le groupe de bordisme $\Omega_1(X)$.
Si $X$ est connexe par arcs, $\Omega_1(X)$ est l’abélianisé du groupe fondamental $\pi_1(X)$, c’est-à-dire le quotient de $\pi_1(X)$ par le sous-groupe engendré par les commutateurs.
Chaque lacet dans $X$ en un certain point base $x_0$ définit un cycle au sens précédent. Deux lacets homotopes définissent des cycles bordants, et on obtient donc un morphisme $h: \pi_1(X,x_0) \to \Omega_1(X)$.
On a vu que toute classe de $\Omega_1(X)$ est représentée par une application ${\bf S}^1 \to X$ dont on peut supposer qu’il s’agit d’un lacet au point base choisi. En d’autres termes, $h$ est surjectif.
Un élément du groupe fondamental qui est dans le noyau de $h$ est représenté par un cycle $f : {\bf S}^1 \to X$ qui se prolonge à une surface orientée dont le bord est un cercle. On introduit les cycles $a_1,b_1,\ldots,a_g,b_g$ comme sur la figure ci-dessous. Le bord de la surface (c’est $f$) est alors homotope au produit de commutateurs : $[a_1,b_1]\cdots[a_g,b_g]$.
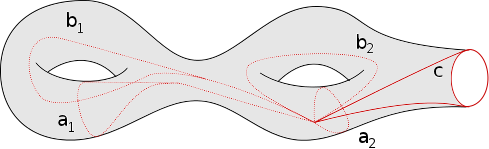
Par conséquent, $[f]\in\pi_1(X)$ est dans le sous groupe engendré par les commutateurs et est donc nul dans l’abélianisé du groupe fondamental. Par conséquent l’application $h$ passe au quotient en un isomorphisme entre l’abélianisé du groupe fondamental et le premier groupe de bordisme.
C.Q.F.D.
Le deuxième groupe de bordisme
Il est très naturel de généraliser la construction ci-dessus, en remplaçant les variétés fermées de dimension 1 par des surfaces. Étant donnée une variété $X$, on appellera donc $2$-cycle de $X$ la donnée d’une application continue $f: S \to X$, où $S$ est une surface fermée orientée.
On dira que deux $2$-cycles $f_0 : S_0 \to X$ et $f_1 : S_1 \to X$ sont bordants, s’il existe une variété compacte orientée $M$ de dimension 3, dont le bord orienté est la réunion de $S_0$ et $\overline{S}_1$ et un prolongement $F$ de $f_0,f_1$ à $M$.
De même que pour les 1-cycles, la réunion disjointe permet de définir une addition sur les 2-cycles, et cette addition passe au quotient par la relation de bordisme. On obtient ainsi un groupe abélien $\Omega_2(X)$, que nous allons étudier succinctement.
Ici encore, une remarque simple s’impose. Toute surface fermée orientée de dimension 2 est le bord d’une variété orientée de dimension 3. C’est clair, car on connait la liste complète des surfaces fermées orientées à homéomorphisme près (voir ici), et que l’on constate que chaque surface de cette liste satisfait la propriété voulue.
Nous pouvons donc affirmer que le deuxième groupe de bordisme $\Omega_2(\{p\})$ d’un point $p$ est le groupe trivial !
Le cas du cercle n’est pas trop difficile.
$\Omega_2({\mathbb S}^1)=0$.
On part d’une application $f:S\to \mathbb{S}^1$ d’une surface vers le cercle. On veut montrer que $S$ est le bord d’une variété de dimension $3$ à laqulle $f$ se prolonge. On choisit une valeur régulière $x$. L’image inverse de cette valeur régulière est une réunion finie de courbes $C_1,\ldots,C_n$. On se place dans $S\times [0,1]$. Pour chaque courbe $C_i$, on considère un disque épaissi $\mathbb{D}^2\times [0,1]$ et on recolle le morceau de bord $(\partial\mathbb{D}^2)\times [0,1]$ sur un voisinage de $C_i\times\{0\}$ dans $S\times \{0\}$. On obtient ainsi une variété $N$ de dimension 3 et une application $N\to S^1$ qui étend $f$ et que l’on note encore $f$. Le bord de $N$ se décompose en deux surfaces : la surface initiale $S$ et une surface $S'$. Sur $S'$, la fonction $f$ évite la valeur régulière $x$.
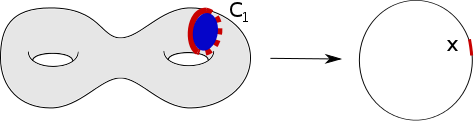
Identifions le complémentaire d’un voisinage de $x$ à l’intervalle $[0,1]$. La fonction $f$ restreinte à $S'$ prend ses valeurs dans $[0,1]$. Il existe une variété $M$ dont le bord est $S'$ et telle que la fonction $f$ s’étende à $M$ (exercice, si vous n’êtes pas inspiré, commencez par le cas de la sphère). Ainsi, en recollant $M$ et $N$ sur leur bord commun on obtient une 3-variété et une application qui prolonge $f$.
Bordisme dans le cas général
Le construction des groupes de bordismes se généralise à des cycles de dimension quelconque. Si $n$ est un entier, et $X$ un espace topologique, on appelle $n$-cycle de $X$ une application continue $f: M\to X$ d’une variété fermée orientée de dimension $n$ vers $X$. Deux cycles sont bordants s’il existe une variété à bord $V$ de dimension $n+1$, et une application continue vers $X$ dont la restriction au bord coïncide avec les deux cycles - en changeant l’orientation du deuxième. De même que précédemment, on définit ainsi un groupe abélien $\Omega_n(X)$ : le $n$-ème groupe de bordisme de $X$.
Mais tout ne se passe pas aussi bien que prévu. Rappelons que notre but initial était de construire des groupes qui mesurent la complexité de la topologie d’une variété. Il va de soi qu’on n’attend pas grand-chose de la topologie d’un point, si bien qu’il est naturel de s’attendre à ce que les groupes associé à un point soit triviaux. La théorie du bordisme ne possède malheureusement pas cette propriété à partir de la dimension 4 : $\Omega_4(\{p\})$ est non trivial car il existe des variétés fermées orientées de dimension $4$ qui ne sont pas le bord de variétés de dimension $5$.
Des propriétés plus élaborées des groupes de bordismes se trouvent dans l’article (plus difficile d’accès, et qui réclame une certaine familiarité avec l’homologie) Quelques propriétés des groupes de bordisme.
