Entre 1895 et 1904, Henri Poincaré a fondé la topologie algébrique — alors appelée Analysis Situs — en publiant une série de six mémoires révolutionnaires. Ces textes fondateurs sont écrits dans le style inimitable de Poincaré : les idées abondent et... côtoient les erreurs. L’ensemble représente un peu plus de 300 pages de mathématiques exceptionnelles.
Plus d’un siècle plus tard, le contenu de ces mémoires reste non seulement d’actualité mais constitue un passage obligatoire pour tout apprenti topologue. Ce site propose au lecteur d’acquérir une vision contemporaine du sujet à travers une approche historique.
Pour démarrer, il suffit de choisir l’une des trois « portes d’entrée » :
Pour étudier l’œuvre de Poincaré, pourquoi ne pas tout simplement commencer par lire Poincaré ? Vous trouverez sur ce site l’intégralité des travaux de Poincaré qui traitent de l’Analysis Situs. D’abord l’« Analysis Situs » proprement dit (paru en 1895 au Journal de l’École Polytechnique), puis les cinq compléments et les cinq notes aux Comptes rendus de l’Académie des Sciences qui l’accompagnent. Ces textes sont regroupés dans la rubrique
Un avertissement s’impose cependant : la lecture des écrits de Poincaré peut s’avérer déroutante pour un mathématicien du XXIe siècle accoutumé à une certaine rigueur post-bourbakiste. Poincaré est parfois disert sur des définitions désormais classiques, parfois elliptique sur des arguments qui s’avèreront problématiques, et il lui arrive de se lancer dans de longues démonstrations aux notations compliquées là où un simple dessin clarifierait beaucoup de choses. Il faut rappeler que les idées foisonnantes contenues dans ces mémoires révolutionnaires n’ont pas encore été « polies » par un siècle de mathématiques.
Pour vous guider dans la lecture de Poincaré, nous proposons ici des commentaires qui suivent de près les textes originaux, pointent les imprécisions — voire les erreurs — de Poincaré et soulignent l’importance que ses idées novatrices auront dans les mathématiques du XXe siècle. Ces commentaires sont regroupés dans la rubrique
Enfin, pour bien comprendre l’œuvre de Poincaré, il est nécessaire d’en comprendre aussi le contexte historique. L’Analysis Situs s’inscrit en effet dans la continuité des travaux de Riemann, Betti, Picard... et des travaux antérieurs de Poincaré lui-même. Nous discutons de la genèse des idées de Poincaré sur l’Analysis Situs dans la rubrique
Dans l’« Analysis Situs », Poincaré crée une science nouvelle. Il s’agit d’étudier la topologie des variétés. Pour convaincre son lecteur de se plonger dans cette étude, Poincaré émaille, bien plus qu’à son habitude, son mémoire et les cinq compléments qui suivront d’exemples bien choisis. À l’instar du Maître, nous proposons ici une découverte de la topologie algébrique par l’étude d’exemples, principalement en dimension $2$ ou $3$.
Dans l’Introduction à l’Analysis Situs par les surfaces, on trouvera une série d’articles qui illustrent certains des grands thèmes de la topologie algébrique dans le cas particulier de la dimension $2$ :
Le groupe fondamental est une des inventions majeures de Poincaré. La rubrique suivante en illustre le calcul sur un certain nombre d’exemples importants :
La plupart des variétés que considèrent Poincaré sont de dimension 3. On peut d’ailleurs considérer Poincaré et Heegaard comme les fondateurs de la topologie de dimension 3. Il est donc naturel que nous leur consacrions une rubrique particulière :
Le plus beau des exemples de Poincaré est certainement celui avec lequel il conclut son cinquième complément. C’est une sphère d’homologie et nous lui consacrons la rubrique :
La topologie algébrique cherche à associer à une variété, ou plus généralement à un espace topologique $X$, un objet algébrique $G(X)$ — typiquement un groupe ou une collection de groupes — qui décrit (en partie) la « forme » de $X$.
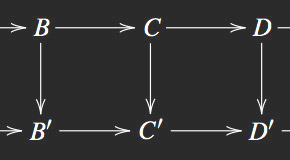
On demande en outre que cette association soit naturelle dans le sens que si $f : X \to Y$ est une application continue, on peut construire un homomorphisme $f_*: G(X) \to G(Y)$ compatible avec les opérations de compositions. En particulier, $G(X)$ est un invariant topologique : si $X$ et $Y$ sont deux espaces topologiques homéomorphes, alors les groupes $G(X)$ et $G(Y)$ sont isomorphes.
On explique ici et là comment, partant de l’exemple des surfaces, Riemann et Betti ont commencé par généraliser la notion d’ "ordre de connexion" d’une surface pour associer aux variétés de dimension quelconque des nombres qui en distinguent certaines. Mais ces notions sont encore vagues et difficiles à formaliser. Un saut conceptuel est réalisé par Poincaré dans son « Analysis Situs » lorsqu’il introduit la notion d’homologie. Toujours dans l’« Analysis Situs », Poincaré introduit également le groupe fondamental, dont on retrace ici la genèse. Enfin, dans le Cinquième complément à l’« Analysis Situs », Poincaré développe une théorie connue de nos jours sous le nom de théorie de Morse, qui consiste à étudier une variété en étudiant les "lignes de niveaux" d’une fonction générique. Ce "cours moderne" propose une présentation de ces trois théories :
Dans l’Analysis Situs et dans le Cinquième complément, Poincaré applique ces théories à l’étude des variétés de dimension $3$, tandis que les Troisième et Quatrième compléments sont consacrés à la topologie des surfaces complexes (de dimension réelle $4$). Nous proposons donc également les cours introductifs suivants :
Enfin, Poincaré développe dans les Premier et Deuxième compléments une version "polyédrale" de l’homologie qui part du principe que les variétés considérées sont triangulées. Nous proposons ici un cours introductif à la notion d’espace PL (piecewise linear) qui contient une démonstration du fait que toute variété lisse peut être triangulée d’une manière essentiellement unique.
- La première, par les œuvres, propose de commencer l’exploration de la topologie algébrique par l’étude commentée des textes originaux de Poincaré.
- La seconde, par les exemples, propose de plutôt commencer par un choix d’exemples pour la plupart tirés des textes de Poincaré.
- Enfin la troisième et dernière « porte d’entrée » propose un véritable cours moderne de topologie, niveau master, regroupé en grands thèmes selon le même « plan » — ou la même anarchie — que le texte source, mais dans lequel la présentation, le style, les démonstrations et les méthodes employées sont celles du XXIe siècle.
Les trois parcours sont évidemment intimement liés ; laissez-vous dériver au fil des nombreux liens.... Une multitude d’animations et de cours filmés illustrent le site. Vous pouvez également les retrouver sur notre chaîne youtube.
Pour aider nos lecteurs, nous avons associé un logo de couleur à chaque article, qui donne une indication approximative du niveau de difficulté. Les voici, par ordre de difficulté croissante :
. Un autre logo
met en avant des textes de nature historique. Nous décrivons plus en détail les principes qui nous ont guidés dans le choix des couleurs sur cette page.
Nous vous proposons également une manière moins sérieuse et plus aléatoire de vous promener sur le site. De nombreux articles sont accompagnés d’une « Anecdote de l’Oncle Henri Paul ». En cliquant sur l’icône ci-contre, vous serez renvoyés sur une liste de ces anecdotes choisies au hasard. Vous pouvez la prendre comme point de départ de votre navigation.
Enfin, pour ceux que notre site n’aura pas lassés de la topologie algébrique, nous proposons une copieuse bibliographie commentée. Cliquez sur l’icône ci-contre pour y accéder.
Henri Paul de Saint-Gervais