|
> Textes originaux > Sur les cycles des surfaces algébriques ; Quatrième complément à l’Analysis (...) > §5. Remarques diverses. Cette page présente la transcription d’une section des Œuvres Complètes de Poincaré. Vous pouvez retrouver nos commentaires par ici. §5. Remarques diverses. |
Dans la suite des démonstrations, nous avons été amené à faire diverses hypothèses au sujet de nos polyèdres. Rappelons-les sommairement :
- Nous avons supposé que le polyèdre que nous avons appelé $P'$ restait homéomorphe à lui-même quand $y$ suivait la coupure $OA_i$ depuis $A_i$ jusqu’en $O$.
- Nous avons comparé la surface de Riemann $S_0$, qui correspond au point $O$, à la surface de Riemann $S(M)$ qui correspond au point $M$, et nous avons dit qu’on pouvait faire correspondre ces deux surfaces point par point. Nous nous sommes servi de cette correspondance pour définir les cycles $U_i$ et $U'_i$ qui correspondent sur $S_0$ à $\Omega_i$ et $\Omega'_i$.
- Nous avons admis ensuite que, quand le point $M$ varie depuis $A_i$ jusqu’à $M_0$, les deux cycles $U_i$ et $U'_i$, d’abord confondus, balayent une certaine région $R$ de $S_0$ à laquelle correspond, sur $S(M_0)$, la région $\sum\theta'_{k}M_{0}F'_{k}$.
- Nous avons admis que, quand le point $M$ décrit successivement les deux lèvres de la coupure $OA_1$, puis les deux lèvres de $OA_2$, . . . , et, enfin, les deux lèvres de la coupure $OA_q$, le cycle mobile $U_i$ (qui revient à sa situation initiale $\Omega_{1}^0$ après avoir occupé une série continue de situations successives) ne balaye pas la surface $S_0$ tout entière.
- Nous avons dit que, si la surface $f(x, y, z) = 0$ a été ramenée, par les procédés de M. Picard, à ne posséder que des singularités ordinaires, à chaque point singulier $A_i$ correspond un seul cycle évanouissant.
- Nous avons supposé que parmi les sommets de $P$ en figurent $m$ qui correspondent à une valeur constante de $x$, par exemple $x = 0$.
La légitimité de ces hypothèses étant à peu près évidente, je n’ai pas voulu interrompre les raisonnements des paragraphes précédents, pour on donner une démonstration explicite. Je n’aurais, d’ailleurs, pu le faire qu’en particularisant le polyèdre $P$, c’est-à-dire en faisant des hypothèses particulières sur la manière dont la surface de Riemann $S$ est subdivisée en polyèdre.
Je crois utile maintenant de revenir sur ces différents points et de faire la démonstration, en adoptant une quelconque de ces hypothèses particulières sur $P$.
On pourrait, par exemple, construire le polyèdre $P$ de la façon suivante :
Commençons par réduire la surface $f = 0$ à n’avoir que des singularités ordinaires.
Donnons à $y$ une valeur quelconque, et considérons la surface de Riemann $S$ correspondante. Cette surface se composera de $m$ feuillets appliqués sur le plan des $x$ (si l’équation $f = 0$ est de degré $m$ en $z$).
Marquons sur le plan des $x$ l’origine $O$ et les points singuliers correspondant aux équations
$$ f = 0, \qquad \frac{df}{dz} = 0.$$
Soit $n$ le nombre de ces points singuliers ; soient $B_1, B_2, \cdots, B_n$ ces points singuliers. Joignons le point $O$ aux $n$ points singuliers $B_1, B_2, \cdots, B_n$ par $n$ coupures $OB_1, OB_2, \cdots, OB_n$ ne se coupant pas mutuellement et se succédant autour du point $O$ dans l’ordre sus-indiqué
On obtiendra la surface de Riemann de la façon ordinaire en raccordant la première lèvre de l’une des coupures sur un des feuillets avec la seconde lèvre de cette même coupure sur un autre feuillet. Par le tracé de ces coupures, la surface de Riemann sera ainsi subdivisée en un polyèdre qui sera notre polyèdre $P$.
On voit que ce polyèdre a $m$ faces (qui sont les $F_i$) et que chacune de ces faces est un polygone de $n$ cotés.
Qu’arrive-t-il maintenant quand on fait varier $y$ ? Les points singuliers $B$ vont se déplacer ; les coupures $OB$ se déformeront, et nous supposerons qu’elles se déforment de façon à ne jamais se couper el à se succéder toujours dans le même ordre autour de $O$. Quand $y$ décrira un petit contour fermé, cette déformation pourra se faire de telle façon que les coupures reviennent à leurs positions primitives, à moins qu’il n’y ait à l’intérieur du contour un point singulier.
Les points singuliers possibles sont de deux sortes :
- D’abord ceux qui correspondent au cas où deux des points singuliers $B$ s’échangent entre eux (un raisonnement de M. Picard montre que si la surface $f = 0$ n’a que des singularités ordinaires, cela ne peut arriver que si le plan $y = const.$ est tangent à la surface $f = 0$) ;
- Puis ceux qui correspondent aux cas où l’un des points singuliers $B$ vient en O.
Les points singuliers de la seconde sorte ne sont pas essentiels, et j’aurais pu les faire disparaître si je n’avais cru plus avantageux de les conserver.
Je désigne tous ces points singuliers par $A_1, A_2, \cdots, A_q$ et je trace dans le plan des $y$ les coupures $OA_1, OA_2, \cdots, OA_q$.
Tant que $y$ ne franchit pas ces coupures $OA$, les coupures $OB$ peuvent se déformer de façon à ne jamais se couper mutuellement, et, par conséquent, de façon que $P$ reste homéomorphe à lui-même, et en même temps de façon que, si $y$ décrit un contour fermé, ces coupures $OB$ reviennent à leurs positions initiales.
Comparons maintenant les configurations des coupures $OB$ quand $y$ se trouve en deux points infiniment voisins sur les deux lèvres d’une coupure $OA_i$.
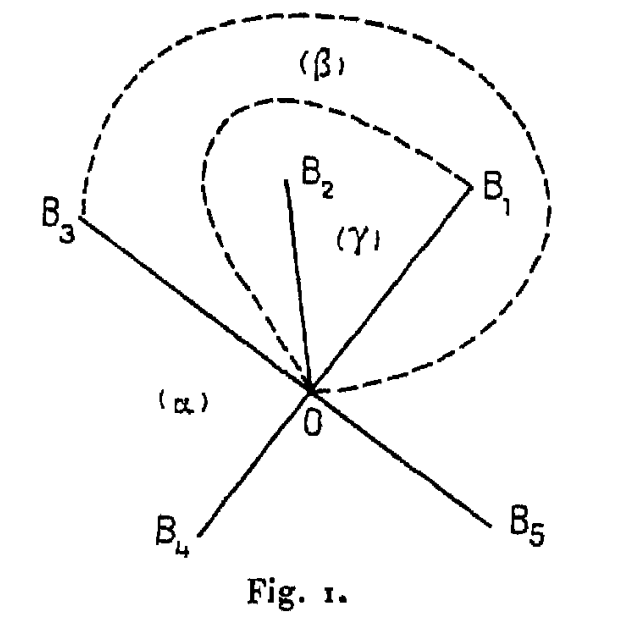
Supposons d’abord que $A_i$ soit un point singulier de la première sorte. Si l’on suppose que la surface $f = 0$ n’a que des singularités ordinaires et que, par conséquent, le plan $y = A_i$ est tangent à $f = 0$ en un point ordinaire, on voit que, quand $y$ tourne autour de $A_i$, deux des points singuliers, par exemple $B_1$ et $B_3$, s’échangent. De plus, si le point $B_1$ permute deux des feuillets de la surface de Riemann, le point $B_3$, qui s’échange avec lui permutera les deux mêmes feuillets de cette surface. J’appellerai ces deux feuillets le premier et le second feuillet de la surface.
Quand $y$ ayant tourné autour de $A_i$ reviendra infiniment près de sa position primitive, mais sur l’autre lèvre de la coupure, on pourra supposer que les coupures $OB$ sont revenues à leur situation primitive, à l’exception des coupures $OB_1$ et $OB_3$. Ces deux dernières coupures, qui occupaient primitivement les lignes $OB_1$ et $OB_3$, marquées en trait plein sur la figure, occuperont finalement les lignes $OB_3$ et $OB_1$ marquées en trait pointillé sur la figure.
On voit que la surface de Riemann peut être subdivisée de deux manières en un polyèdre $P$, les deux modes de subdivision diffèrent l’un de l’autre parce que les lignes pleines $OB_1$ et $OB_3$ sont remplacées par les lignes pointillées $OB_3$ et $OB_1$.
Si l’on superpose les deux modes de subdivision, on aura le polyèdre que j’ai appelé $P'$. On voit que deux des $m$ faces de $P$, celles qui correspondent aux deux premiers feuillets, ont été subdivisées en trois faces partielles désignées sur la figure par les lettres $(\alpha), (\beta), (\gamma)$.
Lorsque $y$ décrira la coupure $OA_i$, les points $B$ se déplaceront d’une manière continue, sans jamais se confondre ni entre eux, ni avec le point $O$ (sauf, bien entendu, quand $y$ revient en $A_i$). Il en résulte que l’on peut déformer toutes nos coupures $OB$ (tant en trait plein qu’en trait pointillé) en évitant qu’elles ne se coupent jamais mutuellement. Cela veut dire que le polyèdre $P'$ restera constamment homéomorphe à lui-même. Dire que $P'$ restera homéomorphe à lui-même, c’est dire que l’on peut faire correspondre point par point la surface $S(M)$ à une autre surface $S(M')$ correspondant à une autre position $M' $de $y$ sur $OA_i$, et en particulier à $S(M')$. On remarquera que la correspondance peut se faire de façon qu’à un point à l’infini sur $S(M)$ corresponde un point à l’infini sur $S(M')$.
Lorsque $y$ vient en $A_i$, le polyèdre $P'$ dégénère : les deux points$B_1$ et $B_3$ se confondent. Il en est de même de la coupure $OB_1$ trait plein avec $OB_3$ pointillé, ainsi que de $OB_1$ pointillé avec $OB_3$ trait plein. Le polygone partiel marqué $ (\beta)$ sur la figure disparaît alors.
Pour aller plus loin, remarquons qu’il y a deux coupures qui se projettent suivant la ligne $OB_1$ en trait plein ; quand on suit la première (que nous appellerons $B_1G$) de $O$ en $B_1$, on a le premier feuillet à gauche et le second à droite ; quand on suit la seconde (que nous appellerons $B_1D$), on a le premier feuillet à droite et le second à gauche. Nous définirons de même $B_3G$ et $B_3D$. Si, au lieu de la ligne $OB_1$ en trait plein, nous envisageons la ligne $OB_1$ en trait pointillé, nous obtiendrons de même deux coupures que j’appellerai $B'_1G$ et $B'_1D$ ; et je définirai encore de même $B'_3G$ et $B'_3D$ .
Nous voyons tout de suite que, quand $y$ tourne autour de $A_i$, les coupures $B_1G$ et $B'_3G$, $B_1D$ et $B'_3D$, $B_3G$ et $B'_1 G$, $B_3D$ et $B'_1D$ se permutent ; que, pour $y = A_i$ $B_1G$ et $B'_3G, \cdots$ se confondent.
Je désignerai par $\beta_1$ celui des polygones partiels $\beta$ qui appartient au premier feuillet si l’on adopte la première subdivision, celle qui correspond au trait plein ; l’autre polygone $ \beta$ s’appellera $\beta_2$
On a alors les congruences
$$\begin{array}{l} \beta_1 \equiv B'_1D - B_1D + B'_3D - B_3D,\\\beta_2 \equiv B'_1G - B_1G + B'_3G - B_3G,\end{array}$$
qui nous apprennent quelles sont celles de nos coupures qui servent de frontières à $\beta_1$ et $\beta_2$.
Considérons la combinaison
$$ \omega = B_3D - B'_1D - B_3G + B'_1G.$$
C’est un cycle de notre surface de Riemann ; quand $y$ tourne autour de $A_i$ elle se change en
$$ B'_1D - B_3D - B'_1G + B_3G,$$
c’est-à-dire en $- \omega$. C’est donc un cycle évanouissant. Il est aisé de voir qu’il n’y en a pas d’autre.
Reprenons maintenant les cycles que nous avons appelés $\Omega_i$ et $\Omega'_i$ au paragraphe II. Soit
$$ \Omega_i = \zeta_1B_1D + \zeta_2B_1G + \zeta_3B_3D + \zeta_4B_3G + H,$$
les $\zeta$ étant des coefficients entiers et $H$ une combinaison d’autres arêtes de $P_1$. Comme le cycle $\Omega_i$ doit être fermé, on devra avoir
$$ \zeta_1 + \zeta_2 = \zeta_3 + \zeta_4 = 0,$$
puisque le sommet $B_i$, par exemple, n’appartient qu’aux deux arêtes $B_1D$ et $B_1G$. Nous aurons ensuite
$$ \Omega'_i = \zeta_1B'_3D + \zeta_2B'_3G + \zeta_3B'_1D + \zeta_4B'_1G + H.$$
Car les arêtes de $P$, autres que $B_1D$, $B_1G$, $B_3D$, $B_3G$ ne sont pas altérées quand $y$ tourne autour de $A_i$, c’est-à-dire que $H$ n’est pas altéré.
On aura donc
| $\Omega_i - \Omega'_i$ | $= \zeta_1(B_1D - B_1G - B'_3D + B'_3G)$ |
| $\quad + \zeta_3(B_3D - BB_3G - B'_1D + B'_1G)$ |
Or, on a
| $(B_1D - B_1G - B'_3D + B'_3G) $ | $ = (B'_1G - B_1G + B'_3G - B_3G) $ |
| $ - (B'_1D - B_1D + B'_3D - B_3D) $ | |
| $ - (B_3D - B'_1D - B_3G + B'_1G)$ |
ou
$$ ( B_1 D - B_1 G - B'_3D + B'_3G) + \omega \equiv \beta_2 - \beta_1;$$
d’où
$$\begin{array}{c} \Omega_i - \Omega'_i + (\zeta_1 - \zeta_3)\omega \equiv \zeta_1(\beta_2 - \beta_1),\\\Omega_i - \Omega'_i \sim (\zeta_3 - \zeta_1)\omega.\end{array}$$
Or, nous avons supposé que le cycle $\Omega_i$ est invariant, c’est-à-dire que
$$ \Omega_i \sim \Omega'_i,$$
ce qui exige $\zeta_1 = \zeta_3$. Dans ces conditions, reprenons la congruence (II.5) du paragraphe II, qui peut s’écrire
$$ \Omega_i = \Omega'_i \equiv \sum \theta'_{k}M F'_k.$$
Quand $y$ (ou $M$) vient en $A_i$, les polygones partiels $\beta_1$ et $\beta_2$ disparaissent, de sorte que le second membre de cette égalité disparaît ; le premier se réduit à $\sum \theta_k ' \alpha_i F_k '$, d’où l’on tire
$$\sum \theta_k ' \alpha_l F_k' = 0.$$
Ainsi se trouve justifié ce que nous avons dit aux pages 407 et suivantes [1].
Supposons maintenant que $A_i$ soit un point singulier de la seconde sorte, et que pour $y= A_i$ le point singulier $B_i$ vienne en $O$.
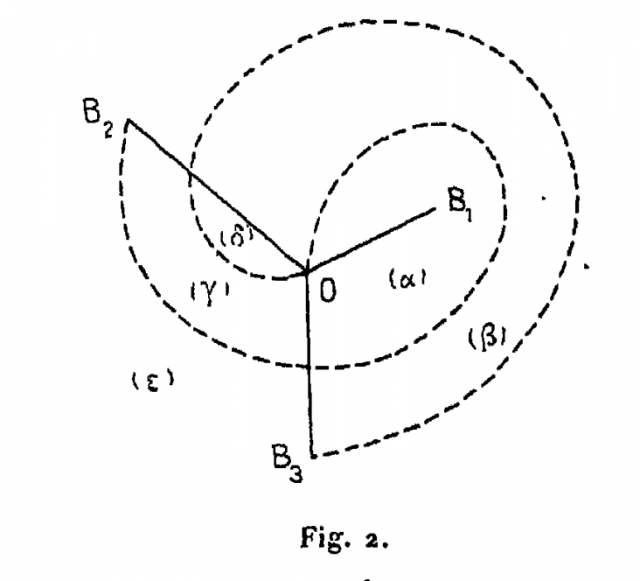
Nous pouvons faire alors une figure analogue à la figure 1 ; pour simplifier, je représenterai trois points singuliers seulement, $B_1$, $B_2$ et $B_3$.
Quand $y$ tourne autour de $A_i$, la coupure $OB_1$ reprend sa situation primitive, mais les coupures $OB_2$ et $OB_3$ (trait plein) se transforment dans les coupures $OB_2$ et $OB_3$ (trait pointillé).
Nous avons deux modes de subdivision et, en les superposant, on a le polyèdre $P'$.
Chaque face de $P$ (c’est-à-dire chaque feuillet de $S$) se trouve subdivisée en un certain nombre de faces partielles. Dans le cas de la figure 2, il y en a cinq désignées sur la figure par $(\alpha )$, $(\beta )$, $(\gamma )$, $(\delta$), ($\varepsilon$).
Il est clair que, quand $y$ décrira la coupure $OA_i$, on peut s’arranger pour que la figure précédente (et par conséquent, le polyèdre $P'$) reste constamment homéomorphe à elle-même.
Je désignerai par $OB_{2}$ et $OB_{3}$ les coupures en trait plein, par $OB_{2}'$ et $OB'_{3}$ les coupures correspondantes en trait pointillé. Je vois que, ces coupures se coupant mutuellement, chacun des tronçons de ces coupures formera l’une des arêtes de $P'$. Je distinguerai, sur chacune de ces coupures, le tronçon terminal, c’est-à-dire celui qui aboutit au point $B_{2}$ ou $B_{3}$.
Quand $y$ vient en $A_{i}$, le polyèdre $P'$ dégénère ; plusieurs de ses arêtes se réduisent à zéro, à savoir l’arête $OB_{1}$ et tous les tronçons de $OB_{2}$, $OB_{3}$, $OB'_{2}$, $OB'_{3}$, les tronçons terminaux exceptés. D’ailleurs, le tronçon terminal de $OB_{2}$ se confond avec celui de $OB'_{2}$ et celui de $OB_{3}$ avec celui de $OB'_{3}$. Il en résulte que les quatre faces partielles $(\alpha )$, $(\beta )$, $(\gamma )$, $(\delta$) disparaissent.
Il n’y a pas ici de cycle évanouissant, le point singulier $A_{i}$ n’étant pas essentiel.
Nous avons sur la figure
$$\begin{array}OB_{2}-OB'_{2} \equiv (\alpha )+(\gamma ) + (\delta), \\OB_{3}-OB'_{3} \equiv (\alpha )+(\gamma ) + (\delta).\end{array}$$
Revenons à notre cycle $\Omega_{i}$ ; nous aurons
$$\Omega_{i} = \sum \zeta_{1} OB_{1} + \sum \zeta_{2} OB_{2} + \sum \zeta_{3} OB_{3}.$$
Je mets le signe $\sum$ parce qu’il y a plusieurs coupures (appartenant à différents feuillets de la surface de Riemann) qui se projettent suivant $OB_{1}$. On aura ensuite
$$\Omega_{i}' = \sum \zeta_{1} OB_{1} + \sum \zeta_{2} OB_{2}' + \sum \zeta_{3} OB_{3}' ;$$
d’où
$$\Omega_{i} -\Omega_{i} ' = \sum \zeta_{2} (OB_{2} -OB_{2}')+ \sum \zeta_{3} (OB_{3} -OB'_{3}), $$
$$\Omega_{i} -\Omega_{i} ' = \sum \zeta_{2} [(\alpha )+(\gamma ) + (\delta)]+ \sum \zeta_{3} [(\alpha )+(\beta ) + (\delta)], $$
et, en comparant à la congruence (II.5) du paragraphe II,
$$\sum \theta_{k}' M F_{k}'= \sum \zeta_{2} [(\alpha )+(\gamma ) + (\delta)]+ \sum \zeta_{3} [(\alpha )+(\beta ) + (\delta)].$$
Quand $y$ vient en $A_{i}$, $(\alpha )$, $(\gamma )$, $ (\delta)$ disparaissent, de sorte qu’il reste
$$\sum \theta_{k}' \alpha_{l}F_{k}'= 0,$$
ce qui justifie encore ici ce que nous avons dit ici.
Supposons que le point $y$ décrive les différentes coupures $OA_{1} , OA_{2}, \ldots , OA_{q}$,les points singuliers $B$ décriront certaines lignes ; nous pouvons supposer qu’aucune de ces lignes ne s’éloigne indéfiniment. En effet, si cela n’était pas, nous trouverions toujours dans le plan des $x$ un petit cercle qui ne serait coupé par aucune de ces lignes, et alors, par un simple changement linéaire de variables, nous pourrions rejeter le centre de ce cercle à l’infini.
Donc, quand le point $y$ décrira successivement les deux lèvres de $OA_{1}$, les deux lèvres de $OA_{2}$, etc., et, enfin, celles de $OA_{q}$, les points singuliers $B$ resteront à distance finie. Nous pourrons donc diriger la déformation des coupures $OB$ de façon que ces coupures restent à distance finie. Le cycle $\Omega_{i}$, qui est formé par une combinaison de ces coupures, restera donc toujours à distance finie ; et il en sera de même du cycle $U_{i}$, qui lui correspond sur $S_{0}$ [car nous pouvons choisir la correspondance de $S (M)$ avec $S_{0}$ de façon qu’à un point à l’infini sur $S(M)$ corresponde un point à l’infini sur $S_{0}$]. Ce cycle ne pourra donc balayer la surface $S_{0}$ tout entière, ce qui justifie ce que nous avons dit ici.
On remarquera enfin que, parmi les sommets de $P$, nous en avons $m$ qui correspondent à $x=0$.
Toutes nos hypothèses se trouvent donc justifiées.