Une invitation à l’homologie persistante

Le but de cet article n’est pas de développer la théorie mais d’encourager le lecteur à apprendre plus, par exemple dans les textes suivants :

• Shmuel Weinberger, What is . . . Persistent Homology ? : Notices of the AMS, January 2011.

• H. Edelsbrunner and J. Harer, Persistent homology : A survey, Surveys on Discrete and Computational Geometry. Twenty Years Later, 257–282 (J. E. Good- man, J. Pach, and R. Pollack, eds.), Contemporary Mathematics 453, Amer. Math. Soc., Providence, Rhode Island, 2008.

• R. Ghrist. Barcodes : The persistent topology of data. Bulletin of the American Mathematical Society, 45:61–75, 2008.

Commençons par faire remarquer, comme le fait Weinberger dans l’article mentionné ci-dessus, que lorsque nous admirons un tableau de Seurat, nous voyons bien plus qu’un grand nombre de points placés les uns à côté des autres : nous voyons une œuvre d’art. Notre cerveau, face à ce genre de tableaux, mais plus généralement face à n’importe quelle image pixelisée, fait en sorte de connecter les points d’une manière ou d’une autre et parvient à définir une « structure topologique », transformant ainsi une donnée discrète en un continuum. L’homologie persistance cherche à formaliser cette idée.

Considérons un ensemble fini $X$ dans l’espace euclidien par exemple. Supposons que cet ensemble soit la « discrétisation » d’un objet lisse. Par exemple, $X$ pourrait être l’ensemble des sommets d’une triangulation très fine d’une surface lisse inconnue. Si $r>0$, on note $X_r$ l’ensemble des points de l’espace qui sont à distance $\leq r$ de l’un des points de $X$. Lorsque $r$ est très petit, $X_r$ n’est que la réunion disjointe d’un grand nombre de petites boules. Lorsque $r$ est très grand, $X_r$ est une grande boule. Lorsque $r$ est un peu plus grand que la distance typique entre un point et ses voisins, on peut penser que $X_r$ sera un voisinage régulier de la surface lisse que l’on cherche à comprendre. Pour chaque entier $i$, on peut calculer l’homologie $H_i(X_r,{\mathbb R})$ et étudier la manière dont son rang évolue avec $r$. Remarquez que si $r_1\leq r_2$, alors $X_{r_1}$ est contenu dans $X_{r_2}$ si bien qu’on a une application $H_i(X_{r_1},{\mathbb R})\to H_i(X_{r_2},{\mathbb R})$ qui décrit l’évolution de la topologie lorsque $r$ varie. C’est le but de l’homologie persistante.

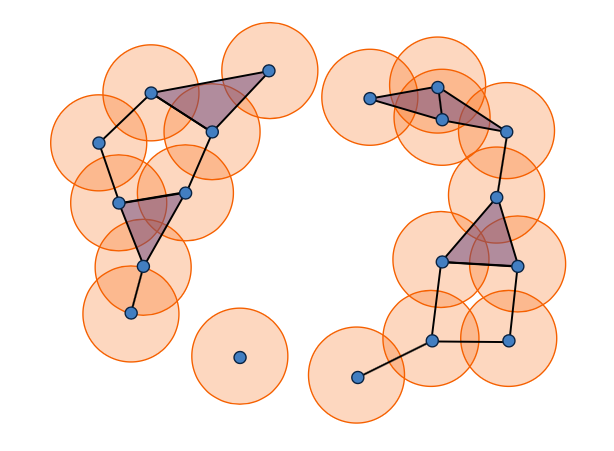
De manière plus proche de l’informatique, on peut construire pour chaque $r>0$ un complexe simplicial $X(r)$ de la manière suivante. Les sommets de $X(r)$ sont les points de $X$ et une partie de $X$ forme les sommets d’un simplexe si les distances mutuelles entre ces points sont $\leq r$. De la même manière, $X(r_1)$ est contenu dans $X(r_2)$ si $r_1 \leq r_2$. Ces complexes sont appelés « Complexes de Rips-Vietoris » de $X$.

Dans l’exemple ci-dessous on part d’un nuage de points dans le plan vaguement organisés le long d’un cercle. On construit alors ce complexe en prenant successivement une distance $r$ "trop petite", puis "trop grande" pour que le complexe de Rips-Vietoris soit homotope à un cercle.

De manière analogue, on peut aussi considérer une variété $M$ et une fonction $f : M \to {\mathbb R}$ (par exemple de Morse) et poser $M_r = f^{-1} (]- \infty, r])$. De la même manière, on a une chaîne d’espaces topologiques indexés par $r$ dont on souhaite comprendre l’homologie.

Formalisons cela.

Définition : Un espace filtré est la donnée d’un espace topologique $X(r)$ pour chaque $r$ et d’une application continue $i_{r_1,r_2} : X(r_1) \to X(r_2)$ pour chaque $r_1 \leq r_2$. On suppose de plus que si $r_1 \leq r_2 \leq r_3$, on a $i_{r_2,r_3} \circ i_{r_1,r_2} = i_{r_1,r_3}$.

D’une manière plus savante, on peut considérer la catégorie $R$ dont les objets sont les $r>0$ et possédant une unique flèche allant de $r_1$ vers $r_2$ pour $r_1 \leq r_2$. Un espace filtré est alors un foncteur de $R$ vers la catégorie des espaces topologiques.

De la même manière, on peut définir des espaces vectoriels filtrés, c’est-à-dire des foncteurs de $R$ vers la catégorie des espaces vectoriels (sur $\mathbb R$ par exemple).

On dira qu’il est de dimension finie si tous les espaces vectoriels qui entrent en jeu sont de dimension finie.

Par exemple, le $i$-ème groupe d’homologie $H_i(X(r), {\mathbb R})$ d’un espace filtré est un espace vectoriel filtré.

Jusqu’à présent, il ne s’agissait que de définitions. Maintenant vient un théorème de classification des espaces vectoriels filtrés, dû à Crawley-Boevey sous la forme présentée :

Soit $I$ un intervalle dans $\mathbb R _+$. Considérons l’espace vectoriel filtré qui est égal à ${\mathbb R}$ pour $r\in I$ et trivial sinon, avec les flèches évidentes.

Théorème : Tout espace vectoriel filtré de dimension finie est isomorphe à la somme directe des espaces filtrés associés à une certaine famille d’intervalles, uniquement définie.

Cette famille d’intervalles est appelée un « code barre ».

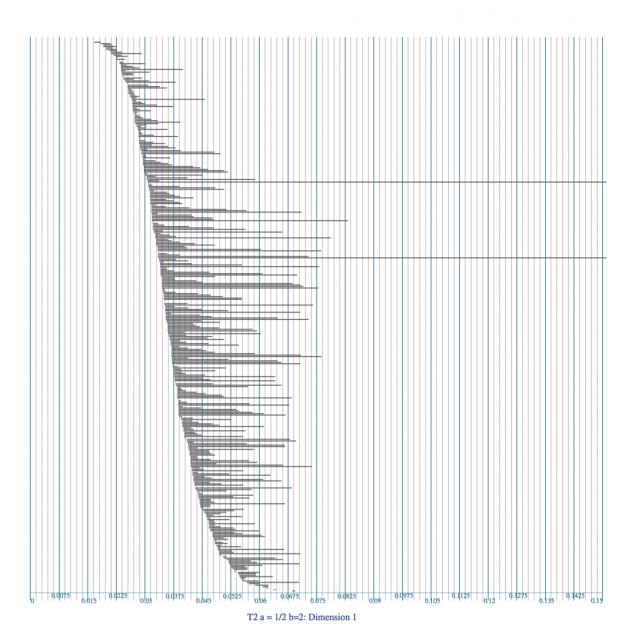
Voici un exemple, extrait de l’article de Weinberger. Un tore de dimension 2, dans l’espace usuel a été discrétisé en un ensemble $X$ de 1400 pixels. On considère l’évolution de $H_1(X(r))$. Voici le code barre correspondant.

Lorsqu’on suit un intervalle d’un code barre, de son origine à son extrémité, on suit une classe de $H_i(X(r))$ en faisant varier $r$ depuis le niveau où la classe en question naît jusqu’au niveau où elle meurt. On voit bien sur cette figure que la grande majorité des intervalles sont courts et deux d’entre eux survivent longtemps. Ce sont bien sûr les deux générateurs de l’homologie du tore.

En général, les grands intervalles sont ceux qui « ont du sens » et les petits forment « le bruit ».

Il est important de remarquer que le passage de $X$ à $X(r)$ se fait facilement sur un ordinateur. Le calcul de l’homologie est alors très simple, numériquement, et le calcul du code barre est également facile. Ainsi, d’une manière complètement automatique, on parvient à extraire de la topologie à partir d’un nuage de points qui pouvait paraître informe.

Il faut encore citer un autre théorème très important. Le code barre d’un ensemble fini $X$ ou d’une fonction de Morse $f:M\to {\mathbb R}$ est étonnamment stable par perturbation, ce qui explique l’intérêt pratique de la théorie.

Par exemple, soit $f(x)= x^2$ comme une fonction de Morse sur $\mathbb R$ et choisissons $i=0$, c’est-à-dire que nous comptons les composantes connexes des sous-niveaux $f(x) \leq r$. Evidemment, il n’y a pas de surprise car tout est connexe. Le code barre de $f$ est donc l’intervalle $\mathbb R ^+$ tout entier.

Modifions $f$ en lui ajoutant du « bruit » en posant $f_{\epsilon} (x)= x^2 + \epsilon \sin ( x / \epsilon^2)$. Si $\epsilon$ est petit, la fonction $f_{\epsilon}$ est proche de $f$ dans la topologie $C^0$ mais elle présente des extrema locaux si bien que les sous-niveaux $f_{\epsilon} \leq r$ peuvent avoir trois composantes connexes. Le $H_0$ n’est plus constant. Cependant, les « bassins d’attraction » des minimas locaux sont petits et en quelque sorte de courte durée (si on pense à $r$ comme le temps, ou comme le niveau d’eau qui monte et qui remplit le sous-niveau). Ainsi le code barre de $f_{\epsilon}$ est constitué de la longue barre $\mathbb R ^+$ auquel s’ajoutent un certain nombre d’intervalles de petite taille. En ce sens, le code barre n’a pas beaucoup changé.

Le théorème de Edelsbrunner, Cohen- Steiner et Harer affirme que si deux fonctions diffèrent au plus de $C$ (donc dans la topologie $C^0$), leurs codes barres sont proches dans le sens précis suivant. On passe d’un code barre à l’autre d’une part en négligeant les intervalles de longueurs $\leq C$ et d’autre part en faisant glisser les extrémités des autres d’une distance inférieure à $C$.

Ainsi, l’application qui associe un code barre à une fonction, ou à un ensemble fini, est continue dans un sens très fort.

Essayez de démontrer le théorème de Edelsbrunner, Cohen- Steiner et Harer.

Même dans le cas « classique » d’une fonction de Morse, même sur une surface, ces codes barres sont intéressants. Il définissent des accouplements entre les valeurs critiques, qui localisent les lieux de naissance et de mort des classes d’homologie. Le lecteur est encouragé à faire quelques dessins.