Théorie de Morse et homologie

On a montré ici qu’une fonction de Morse $f$ sur une variété compacte $M$ induisait une décomposition en anses de celle-ci avec une anse d’indice $k$ par point critique d’indice $k$. Voici la version homotopique de cet énoncé, basée sur la version homotopique des théorèmes sur l’évolution de la topologie des sous-niveaux d’une fonction de Morse :

Pour une démonstration complète de ce résultat, nous renvoyons au livre :

• Milnor, John. Morse Theory, Annals of Mathematics Studies 51, Princeton University Press, 1963.

Pour certaines variétés très simples, ceci permet, en choisissant bien la fonction de Morse, de déterminer complètement l’homologie de la variété. C’est notamment le cas de l’espace projectif complexe. L’étude qui suit est largement inspirée du livre de Milnor susmentionné.

Homologie de l’espace projectif complexe via la théorie de Morse

On rappelle que l’espace projectif complexe $P^n_{\mathbf{C}}$ est par définition l’ensemble des $(n+1)$-uplets de nombres complexes non tous nuls, à homothétie près. Il revient donc au même de penser à $P^n_{\mathbf{C}}$ comme l’ensemble des $(n+1)$-uplets de nombres complexes $(z_0, \cdots, z_n)$ tels que $\sum_i |z_i|^2 =1$.
Nous désignerons comme de coutume par $[z_0 : \cdots : z_n]$ les coordonnées homogènes d’un point de $P^n_{\mathbf{C}}$.

Donnons-nous $(n+1)$ nombres réels distincts $c_i$, par exemple $1, 2, \cdots, n+1$, et considérons la fonction $f$ définie sur $P^n_{\mathbf{C}}$ et à valeurs réelles par

$$f([z_0 : \cdots : z_n]) = \sum_i c_i |z_i|^2.$$

Nous allons vérifier ci-dessous que la fonction $f$ a exactement $(n+1)$ points critiques non dégénérés d’indices $0,2,\cdots,2n$. Il découle alors du théorème ci-dessus que $P^n_{\mathbf{C}}$ a le type d’homotopie d’un CW-complexe obtenu (à partir de l’ensemble vide) par attachement d’une cellule de dimension 0, puis d’une cellule de dimension 2... puis d’une cellule de dimension 2n. On conclut finalement que les seuls groupes d’homologie entières de $P^n_{\mathbf{C}}$ non nuls sont :

$$\text{H}_i(\text{P}^n_{\mathbf{C}}) = \mathbf{Z} \quad \text{pour tout} \ i = 0, 2, \cdots, 2n.$$

On donne plus de détails ici.

Pour étudier les points critiques de notre fonction $f$, considérons un système de coordonnées locales adapté. Désignons par $U_k$ l’ensemble des points de $P^n_{\mathbf{C}}$ dont la coordonnée $k$ homogène est non nulle. On peut donc écrire dans une telle carte

$$|z_k| \frac{z_i}{z_k} = x_i + i y_i,$$

en notant $x_i, y_i$ les fonctions coordonnées qui définissent ainsi un difféomorphisme de $U_k$ sur la boule unité ouverte de $\mathbf{R}^{2n}$.
Par ailleurs, on a bien sûr que $|x_i|^2+|y_i|^2= |z_i|^2$ et $|z_k|^2 = 1 - \sum_{i\neq k}|z_i|^2$, et donc

$$f([z_0 : \cdots : z_n]) = c_k + \sum_i (c_i-c_k)(x_i^2+y_i^2)$$

sur toute la carte $U_k$.
Il apparaît alors évident $f$ n’a qu’un seul point critique sur toute la carte $U_k$, c’est le point $[0:\cdots : 1 : \cdots : 0]$ au centre de la carte. Par ailleurs, c’est un point critique non dégénéré dont l’indice se lit facilement puisque c’est deux fois le nombre de $i$ tels que $c_i-c_k<0$.

$$ $$

Dans le cas général en revanche, sans plus d’information sur la façon dont les cellules sont attachées, on ne peut pas calculer complètement l’homologie. On peut néanmoins obtenir des informations sur les nombres de Betti en termes des points critiques de la fonction sous forme d’inégalités, appelées inégalités de Morse. C’est sous cette forme qu’apparaissait le lien entre fonctions de Morse et topologie à l’origine de la théorie. Dans sa version plus contemporaine, la théorie de Morse permet en fait aussi de retrouver complètement l’homologie de la variété à partir du complexe de Morse, défini à partir des points critiques de $f$ et des trajectoires de (pseudo)-gradient les reliant.

Inégalités de Morse

Soit $M$ une variété compacte et $f$ une fonction de Morse sur $M$. On note $C_i$ le nombre de points critiques d’indice $i$ et $b_i$ le $i^e$ nombre de Betti de $M$, c’est-à-dire le rang du $i^e$ module d’homologie $H_i(M)$ (voir la rubrique Homologie pour des définitions précises concernant l’homologie et les nombres de Betti).

Quelques exemples/remarques pour commencer. Si on pense au cercle unité dans le plan euclidien et à la projection sur l’axe vertical (c’est-à-dire la fonction sinus), on voit sans difficulté que cette fonction a deux points critiques non dégénérés, le pôle sud et le pôle nord, l’un étant d’indice 0 et l’autre d’indice 1. Par ailleurs pour le cercle, $b_0$ vaut 1 (le cercle est connexe) et $b_1=1$ (le lacet non trivial est un générateur). Les inégalités du théorème sont dans ce cas des égalités et la caractéristique d’Euler est bien nulle.

On peut faire le même exemple avec la sphère $\mathbf{S}^2$ dans $\mathbf{R}^3$ : cette fois notre fonction projection sur l’axe a un point critique d’indice 0 (toujours le pôle sud) et un autre d’indice 2 (le pôle nord). Du côté de l’homologie, $b_0=b_2=1$ (par connexité et dualité), et $b_1$ est nul (il suffit de dire que la sphère est simplement connexe). Là encore, les inégalités sont des égalités et la caractéristique d’Euler est 2.

On laisse le lecteur poursuivre le même raisonnement avec les sphères de dimension supérieure. Ne pas oublier non plus de s’exercer avec les surfaces de genre plus grand, à commencer par le tore bien sûr.

Remarquons qu’en partant de la sphère $\mathbf{S}^2$ bien ronde et en la cabossant un peu, il n’est pas difficile de faire apparaître plein de points critiques d’indice 0, et donc on comprend pourquoi il s’agit en général d’inégalités. Pas de contradiction pour autant au moment de calculer la caractéristique d’Euler, car en cabossant notre surface, nous avons inévitablement fait apparaître des points critiques d’indice 1 également...

En fait, on peut raffiner le théorème précédent comme suit :

On dit « raffiner » car additionner ces dernières inégalités aux rangs $i$ et $i-1$ redonne $b_i\le C_i$, tandis que les comparer pour $i>n$ donne l’égalité du théorème précédent.

$$ $$

Démonstration du corollaire.
Puisque $b_{i+1}\leq C_{i+1}$, il est donc évident que si $C_{i+1}$ est nul, il en est de même de $b_{i+1}$. En combinant alors les deux inégalités

$$b_i-b_{i-1}+ \cdots \pm b_0 \leq C_i-C_{i-1}+ \cdots \pm C_0.$$

et

$$b_{i+1}-b_i+ \cdots \pm b_0 \leq C_{i+1}-C_i+ \cdots \pm C_0.$$

on en déduit donc (puisque $C_{i+1}=b_{i+1}=0$), que

$$b_i-b_{i-1}+ \cdots \pm b_0 = C_i-C_{i-1}+ \cdots \pm C_0.$$

Si de plus on suppose que $C_{i-1}$ est nul, alors $b_{i-1}$ est aussi nul, et on utilise le même argument que précédemment pour en déduire que

$$b_{i-2}-b_{i-3}+ \cdots \pm b_0 = C_{i-2}-C_{i-3}+ \cdots \pm C_0.$$

En combinant ces deux dernières égalités, on en déduit finalement que $b_i=C_i$.

Application : calcul de l’homologie de $\mathbf{P}^n_{\mathbf{C}}$.
Au début de cet article, l’homologie de $\mathbf{P}^n_{\mathbf{C}}$ est calculée grâce à une fonction de Morse explicitement construite. Rappelons que cette fonction de Morse a la propriété d’avoir exactement $(n+1)$ points critiques non dégénérés d’indices $0,2,\cdots,2n$. Le corollaire précédent permet de conclure immédiatement. Les seuls groupes d’homologie non nuls de $\mathbf{P}^n_{\mathbf{C}}$ sont de rang 1 en dimension pair entre 0 et $2n$.

Démonstration des inégalités de Morse.
Si on considère des inclusions d’espaces $Z \subset Y \subset X$, en utilisant la suite exacte longue d’homologie pour le triplet $(Z,Y,X)$, on montre que

$$b_i(X,Z) \leq b_i(X,Y) + b_i(Y,Z) \quad \text{et} \quad \chi(X,Z) = \chi(X,Y) + \chi(Y,Z),$$

d’où on déduit par récurrence que pour toute suite croissante $\emptyset=X_0\subset X_1\subset\dots\subset X_k=M$ de sous-espaces de $M$,

$$b_i(M)=b_i(X_n,X_0)\le \sum_{j=1}^k b_i(X_j,X_{j-1})\quad \text{et} \quad \chi(M)= \sum_{j=1}^k \chi(X_j,X_{j-1}).$$

Quitte à modifier un peu $f$, on peut supposer que chacun de ses niveaux critiques contient un unique point critique. On applique alors ce qui précède à une suite de sous-niveaux réguliers $\emptyset=M^{a_0}\subset M^{a_1}\subset\dots\subset M^{a_k}=M$ tels que $f^{-1}(]a_{j-1},a_{j}[)$ contienne un unique point critique de $f$, d’indice $\lambda_j$. D’après l’étude de l’évolution des sous-niveaux, on a $b_i(M^{a_j},M^{a_{j-1}}) = 1$ si $i=\lambda_j$, et 0 sinon, de sorte que l’inégalité ci-dessus devient alors

$$b_i(M) \leq \sum_{j=1}^k b_i(M^{a_j},M^{a_{j-1}}) = C_i,$$

tandis que l’égalité pour la caractéristique d’Euler devient

$$\chi(M) = \sum_{j=1}^k \chi(M^{a_j},M^{a_{j-1}}) =\sum_{i=1}^n(-1)^i C_i.$$

Comme indiqué précédemment, on peut raffiner les inégalités précédentes, avec un argument analogue appliqué à la somme alternée

$$S_i = b_i-b_{i-1}+ \cdots \pm b_0,$$

qui vérifie également une formule de sous-additivité, à savoir, pour tout triplet $Z\subset Y\subset X$,

$$S_i(X,Z) \leq S_i(Y,Z) + S_i(X,Y).$$

Le lecteur aura plaisir à démontrer cette assertion en utilisant comme précédemment la suite exacte longue en homologie pour le triplet $(Z,Y,X)$ et en appliquant successivement le théorème du rang.

Une preuve alternative des inégalités de Morse, qui insiste plus sur leurs aspects algébriques, est expliquée dans notre article « Algèbre des inégalités de Morse ».

Complexe de Morse

Ici, on explique rapidement comment construire, à partir d’une fonction de Morse $f$ sur une variété $M$ et d’un champ de gradient associé convenablement choisi, un complexe dont l’homologie est celle de la variété (et ne dépend en particulier ni de la fonction de Morse ni de la métrique choisie).

Pour $k$ compris entre $0$ et $n$, dimension de la variété, on définit $C_k$ comme le $\mathbb{Z}$-module libre engendré par les points critiques d’indice $k$ de $f$. La définition des applications de bord $\partial:C_k\to C_{k-1}$ est plus délicate. Pour les définir, on choisit une métrique riemannienne sur $M$ qui coïncide avec la métrique euclidienne standard dans des cartes de Morse au voisinage des points critiques. On note $X$ l’opposé du gradient de $f$ pour cette métrique et on s’intéresse au flot $\phi_t$ de $X$. Soit $x\in M$, alors la trajectoire $t\to\phi_t(x)$ tend vers des points critiques de $f$ quand $t$ tend vers $\pm\infty$. Voici quelques exemples de trajectoires sur une sphère non standard.

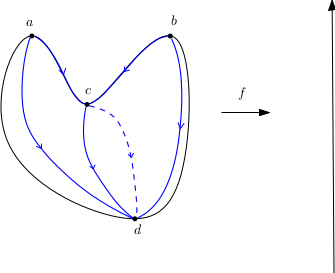
Soit $a$ un point critique, sa variété stable $W^s(a)$ est définie par

$$W^s(a)=\{x\in M, \lim_{t\to\infty}\phi_t(x)=a\}$$

et sa variété instable par

$$W^u(a)=\{x\in M, \lim_{t\to-\infty}\phi_t(x)=a\}.$$

On dit que $X$ satisfait la condition de Smale si les variétés stables et instables de tous les couples de points critiques sont transverses. Dans la situation suivante, la condition de Smale n’est pas vérifiée.

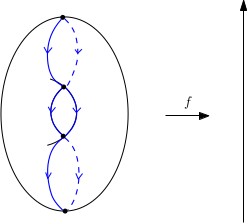
Par contre, si on penche un peu le tore, la condition de Smale est satisfaite !

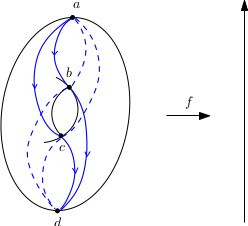
Cette condition est générique et on supposera dans toute la suite qu’elle est vérifiée.

On définit alors l’application de bord comme suit : étant donné un point critique $a$ d’indice $k$, on pose

$$\partial(a)=\sum_{b\in crit_{k-1}}n(a,b) b$$

où $n(a,b)$ est le nombre de trajectoires de $X$ descendant de $a$ à $b$. Les trajectoires sont comptées avec un signe. Déterminer le signe d’une trajectoire est un peu délicat et la description qui suit peut être ignorée en première lecture.

Pour compter les trajectoires avec signe, on fixe une orientation des espaces stables en chaque point critique [1], cette orientation induit une orientation des variétés stables et instables ($M$ est supposée orientée), on place alors sur un niveau régulier $c$ de $f$ entre $f(a)$ et $f(b)$ et $n(a,b)$ correspond au nombre d’intersection de la variété stable de $b$ et de la variété instable de $a$ restreintes à $f^{-1}(c)$.

Nous avons alors le théorème fondamental suivant :

Pour la preuve de ce résultat, on renvoie par exemple à :

• Augustin Banyaga, David Hurtubise. Lectures on Morse Homology, Kluwer Academic Publishers (2004).
• François Laudenbach. Symplectic Geometry and Floer Homology, Ensaios Matemáticos 7 (2004), 1-50 (Section 3).

Terminons par deux exemples. Dans le cas de la sphère (non standard),

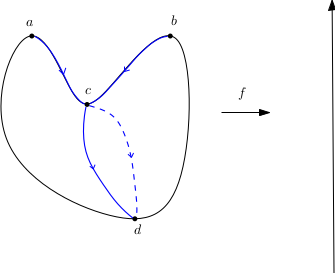
on obtient $\partial a = c$, $\partial b = -c$ et $\partial c=0$ (attention aux conventions d’orientations). On retrouve donc bien l’homologie attendue. Dans le cas du tore

toutes les différentielles des points critiques sont nulles (encore les conventions d’orientations) et on retrouve encore l’homologie désirée.

L’homologie de Morse est à la base des homologies « à la Floer » mais cela dépasse le cadre de ce site...